Download Scientific Notation

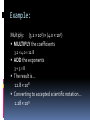
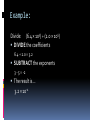
Section 1.2
SCIENTIFIC NOTATION
Why use it?
 Some numbers are too big or too small to
write using regular form (also called standard
notation)
 Using Scientific Notation often makes it
easier to multiply or divide numbers without
a calculator
 How would you express an answer of
50000 L to only 3 significant digits?
What does it look like?
 Scientific Notation takes the form
Coefficient × 10exponent
Coefficient is always ≥ 1 but < 10.
The exponent is either a positive or negative
whole number.
What does the exponent tell me?
 Exponents less than 0
 These are numbers that are smaller than 1
 Exponents equal to 0
 The number is between 1 and 10.
 Exponents greater than 0
 The number is greater than 10.
Here’s how to use it:
 Take any number, let’s say…
503
 To turn it into scientific notation, place a decimal
point that results in a number between 1 and 10.
5.03
 You moved it 2 places to the left. Remember
that number.
And now for the exponent…
5.03
is what you got from the previous step. You
moved the decimal point 2 places to the left to
get there, so use 2 for your exponent.
5.03 × 102
One more example
 Turn this number into scientific notation:
0.0000341
 To turn it into scientific notation, move the
decimal place until you get the coefficient!
0.00003.41
 You moved it 5 places to the right. Remember
that number.
And now for the exponent…
3.41
is what you got from the previous step. You
moved the decimal place 5 places to the right to
get there, so use -5 for your exponent.
3.41 × 10-5
Multiplying Scientific
Notation
 When multiplying two scientific notation
numbers together…
 MULTIPLY the coefficients
 ADD the exponents
Example:
Multiply: (3.2 × 103) × (4.0 × 105)
 MULTIPLY the coefficients
3.2 × 4.0 = 12.8
 ADD the exponents
3+5=8
 The result is…
12.8 × 108
 Converting to accepted scientific notation…
1.28 × 109
Dividing Scientific Notation
 When dividing two scientific notation
numbers…
 DIVIDE the coefficients
 SUBTRACT the exponents
Example:
Divide: (6.4 × 103) ÷ (2.0 × 105)
 DIVIDE the coefficients
6.4 ÷ 2.0 = 3.2
 SUBTRACT the exponents
3 - 5 = -2
 The result is…
3.2 × 10-2
Scientific Notation and
significant digits
 6.23 x 102 K has how many sigfigs?
 1.00023 x 10-2 m?
 How would you express an answer of
50000 L to 3 significant digits?
 5.00 x 104 L (this cannot be done using
standard notation)
Useful exponents to memorize
 10-9
 10-6
 10-3
 10-2
nanomicromillicenti-
(billionth)
(millionth)
(thousandth)
(hundredth)
kilomegagiga-
(thousands)
(millions)
(billions)
 Base
 103
 106
 109