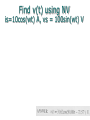* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download EE2003 Circuit Theory
Radio transmitter design wikipedia , lookup
Operational amplifier wikipedia , lookup
Index of electronics articles wikipedia , lookup
Electronic engineering wikipedia , lookup
Power electronics wikipedia , lookup
Schmitt trigger wikipedia , lookup
Switched-mode power supply wikipedia , lookup
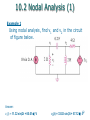
Surge protector wikipedia , lookup
Regenerative circuit wikipedia , lookup
Current source wikipedia , lookup
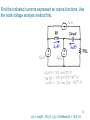
Topology (electrical circuits) wikipedia , lookup
Power MOSFET wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Rectiverter wikipedia , lookup
Current mirror wikipedia , lookup
Valve RF amplifier wikipedia , lookup
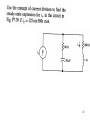
Flexible electronics wikipedia , lookup
Integrated circuit wikipedia , lookup
Two-port network wikipedia , lookup
Opto-isolator wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
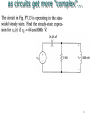
Circuit Theory Chapter 9B Sinusoidal Steady-State : Node Voltage, Mesh Current, Thevenin Copyright © The McGraw-Hill Companies, Inc. Permission required for reproduction or display. 1 Sinusoidal Steady-State Analysis Chapter 10 10.1 10.2 10.3 10.4 10.5 10.6 Basic Approach Nodal Analysis Mesh Analysis Superposition Theorem Source Transformation Thevenin and Norton Equivalent Circuits 2 10.1 Basic Approach (1) Steps to Analyze AC Circuits: 1. 2. 3. Transform the circuit to the phasor or frequency domain. Solve the problem using circuit techniques (nodal analysis, mesh analysis, superposition, etc.). Transform the resulting phasor to the time domain. Time to Freq Solve variables in Freq Freq to Time 3 as circuits get more "complex"... 4 ...we'll start writing matlab scripts to solve them 5 Complex Polar Helper Functions download into your working folder • ang.m: helps convert angle to rect Here's how to use it: --> 5*ang(45) ans = 3.5355 + 3.5355i 6 magPhs.m – prints in polar --> magPhs(40 + 30j) 50.000 < 36.87 this just PRINTS in polar. Do not use in calculations. Only at end to get polar 7 Find v(t) using NV is=10cos(wt) A, vs = 100sin(wt) V 8 % NVdemo.m % solution to first NV demo in lecture 9b % time domain values w = 50000; C = 9e-6; L=100e-6; R1=5; R2=20; % phasor domain Is=10*ang(0); Vs=100*ang(-90); ZC = -j/(w*C); ZL = j*w*L; V = (Is + Vs/20)/(1/5 + 1/ZC + 1/ZL +1/20) magPhs(V); % print out V in polar form 9 10.2 Nodal Analysis (1) Example 1 Using nodal analysis, find v1 and v2 in the circuit of figure below. Answer: v1(t) = 11.32 sin(2t + 60.01) V 10 v2(t) = 33.02 sin(2t + 57.12) V % % % w C L NVdemo2.m time domain = 2; = 0.2; = 2; % phasor domain Is = 10*ang(-90); ZC = -j/(w*C); ZL = j*w*L; % % % % % Node eq at -Is + V1/2 Node eq at (V2-V1)/ZC Vx = V1 V1: + (V1-V2)/ZC V2: + V2/ZL + (V2-3*Vx)/4 % % % % % Rearranging V1( 0.5 + 1/ZC) - V2/ZC = Is V1( -1/ZC -3/4) + V2(1/ZC + 1/ZL +1/4) = 0 A * Vunknown = B 1/R * V = I -> 1/Z *V = I -> Y*V = I % matrix of admittances between nodes: Y = [ .5 + 1/ZC , -1/ZC ; -1/ZC - 3/4, 1/ZC + 1/ZL + 1/4 ] I = [ Is ; 0] V = inv(Y)*I % V = Y\I % solution vector of node voltages magPhs(V) % Shows V1 and V2 in polar form 11 Output from NVdemo2 Y= 0.5000 + 0.4000i 0.0000 - 0.4000i -0.7500 - 0.4000i 0.2500 + 0.1500i I= 0.0000 - 10.0000i 0 V= 9.8113 - 5.6604i 27.7358 - 17.9245i 11.327 < -29.98 33.024 < -32.87 (rectangular form) (polar form) Find the indicated currents expressed as cosine functions. Use the node voltage analysis method first. 13 i1(t) = cos(5t - 30°) A; i2(t) = 0.658cos(5t + 14.6°) A 14 Mesh Analysis Use mesh current analysis to find the phasor voltages V1 and V2. 15 V1 = 22.9∠110° V; V2 = 19.6∠-101° V Solution to previous in Freemat % I*Z = V in phasor domain Z = [ -2j, 5+3j ; -1,1] V = [0; 10*ang(0) ] I = inv(Z)*V magPhs(I(1)) magPhs(I(2)) V1 = -2j*I(1) magPhs(V1) V2 = 5*I(2) magPhs(V2) 16 Output from previous slide Z = -0.0000 - 2.0000i -1.0000 + 0.0000i V = 0 10.0000 + 0.0000i I = -10.7692 - 3.8462i -0.7692 - 3.8462i 11.435 < -160.35 3.922 < -101.31 V1 = -7.6923 + 21.5385i 22.871 < 109.65 V2 = -3.8462 - 19.2308i 19.612 < -101.31 5.0000 + 1.0000 + 3.0000i 0.0000i (rectangular) (polar) (rectangular) (polar) 17 10.3 Mesh Analysis (1) Example 2 Find Io in the following figure using mesh analysis. Answer: Io = 1.19465.44 A 18 Find the indicated mesh currents. 19 I1 = 3.88 ∠ -153° A; I2 = 3.48 ∠ 176° A 20 21 10.4 Superposition Theorem (1) When a circuit has sources operating at different frequencies, • The separate phasor circuit for each frequency must be solved independently, and • The total response is the sum of timedomain responses of all the individual phasor circuits. 22 10.4 Superposition Theorem (2) Example 3 Calculate vo in the circuit of figure shown below using the superposition theorem. Vo = 4.631 sin(5t – 81.12) + 1.051 cos(10t – 86.24) V 23 10.5 Source Transformation (1) 24 10.5 Source Transformation (2) Example 4 Find Io in the circuit of figure below using the concept of source transformation. Io = 3.28899.46 A 25 10.6 Thevenin and Norton Equivalent Circuits (1) Thevenin transform Norton transform 28 Thevenin: Find the Thevenin equivalent circuit at the terminals F-G. Express all complex values in your solution in both rectangular and polar form. 29 VTH = 250 - j200 V = 320 ∠ -38.7° V; ZTH = 100 + j20 Ω = 102 ∠ 11.3° Ω 10.6 Thevenin and Norton Equivalent Circuits (2) Example 5 Find the Thevenin equivalent at terminals a–b of the circuit below. Zth =12.4 – j3.2 VTH = 18.97-51.57 V 31 32 1) Use nodal analysis to determine which impedance element has the lowest voltage magnitude across its terminals. 3.3 kΩ resistor 33 (voltage magnitude is 2.07 V, where other voltage magnitudes are 25.6 V and 13.7 V) 2) Find the indicated mesh currents. 34 I1 = 3.88 ∠ -153° A; I2 = 3.48 ∠ 176° A 3) Apply repeated source transformations to reduce this to an equivalent circuit at the terminals G-H. The simplified circuit will consist of a voltage source in series with two series-connected passive elements. 35 Voltage source = 1140cos(60t + 68.4°); 200 Ω resistor; 74.1 μF capacitor 4) Find the Norton equivalent circuit at the terminals Q-R. Express all complex values in your answer in both rectangular and polar form. 36 IN = 0.769 - j1.15 A = 1.39∠-56.3° A; ZN = 0.523 - j1.27 W = 1.38∠-67.7° W 37 38