Download Behavior-Based Robotics

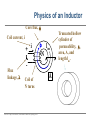
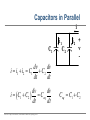
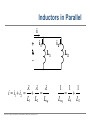
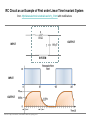
EE 1106: Introduction to EE
Freshman Practicum
Lecture-Lab: Introduction to signals
and systems, RLC dynamical circuit
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
Signals and Systems
– Signal:
• Any time dependent physical quantity
• Constant – DC, Variable - AC
• Electrical, Optical, Mechanical
– System:
• Object in which input signals interact to
produce output signals.
• Linear System has some have fundamental
properties that make it predictable:
– Sinusoid in, sinusoid out of same frequency
(when transients settle)
– Double the amplitude in, double the amplitude
out (when initial state conditions are zero)
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
u(t)
?
x(t)
y(t)
System Modeling
• Building mathematical models based on
observed data, or other insight for the system.
– Parametric models (analytical): ODE, PDE
– Non-parametric models: graphical models plots, look-up cause-effect tables
– Mental models – Driving a car and using the
cause-effect knowledge
– Simulation models – Many interconnect
subroutines, objects in video game
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
Types of Models
• White Box
– derived from first principles laws: physical,
chemical, biological, economical, etc.
– Examples: RLC circuits, MSD mechanical
models (electromechanical system models).
• Black Box
– model is entirely derived from measured data
– Example: regression (data fit)
• Gray Box – combination of the two
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
White Box Systems: Electrical
• Defined by Electro-Magnetic Laws of
Physics: Ohm’s Law, Kirchoff’s Laws,
Maxwell’s Equations
• Example: Resistor, Capacitor, Inductor
i
i
i
u
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
L
C
R
u
u
Physics of an Inductor
Core flux, f
Coil current, i
i
+
l
Flux
linkage, l
Coil of
N turns
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
f l
m
N
A
Truncated hollow
cylinder of
permeability, m,
area, A, and
length lm.
Voltage Drop Across Inductor
i
L
+ v + l -
Note Passive Sign
Convention
d l d  m N 2 Ai  m N 2 A di
v
 

dt dt  lm 
lm dt
m N2A
di
L
vL
lm
dt
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
Energy in an Inductor
i
L
+ v + l -
di
p  vi  Li
dt
p dt  dw  Li di
Stored Energy
1 2
W   Li di  Li
2
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
Physics of a Capacitor
Plate area, A
Plate separation
distance, g
g
i, q
A
e
Current, i, and
Charge, q.
+
v
-
Dielectric material of
permittivity, e.
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
Voltage
across
plates
Physics of a Capacitor
dq d  e Av  e A dv
 

Current: i 

dt dt  g  g dt
eA
C
Capacitance:
g
i, q
Note Passive
Sign Convention:
C
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
+
v
-
dv
iC
dt
Energy in a Capacitor
i
C
dv
p  vi  Cv
dt
Stored Energy:
+
v
-
p dt  dw  Cv dv
1 2
W   Cv dv  Cv
2
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
Inductors in Series
i
L1
L2
+ v1 - + v2 +
v
-
di
di
v  v1  v2  L1  L2
dt
dt
di
di
v   L1  L2   Leq
dt
dt
Leq  L1  L2
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
Capacitors in Parallel
i
C1
i1
C2
i2 +
v
-
dv
dv
i  i1  i2  C1  C2
dt
dt
dv
dv
i   C1  C2   Ceq
dt
dt
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
Ceq  C1  C2
Inductors in Parallel
i
i1
+
l
-
i  i1  i2 
l
L1

i2
L1
l
L2
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015

l
Leq
L2
1
1 1
 
Leq L1 L2
Capacitors in Series
q C1
q
C2 q
+ v2 + v1 +
v
-
q
q
q
v  v1  v2  

C1 C2 Ceq
1
1
1
 
Ceq C1 C2
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
RLC Circuit as a System
R
u
u
1
u
u
2
C
u(t)
RLC
q(t)
3
L
Kirchoff’s Voltage Law (KVL):
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
i(t)
RC Circuit as an Example of First order Linear Time
Invariant System
from http://www.electronics-tutorials.ws/rc/rc_1.html with modifications
OUTPUT
SYSTEM
INPUT
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
RC Circuit as an Example of First order Linear Time Invariant System
from http://www.electronics-tutorials.ws/rc/rc_3.html with modifications
OUTPUT
INPUT
SYSTEM
INPUT
OUTPUT
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
RC Circuit as an Example of First order Linear Time Invariant System
from http://www.electronics-tutorials.ws/rc/rc_3.html with modifications
OUTPUT
INPUT
SYSTEM
INPUT
OUTPUT
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
RC Circuit as an Example of First order Linear Time Invariant System
from http://www.electronics-tutorials.ws/rc/rc_3.html with modifications
OUTPUT
INPUT
SYSTEM
INPUT
OUTPUT
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
Integrator and Low Pass Filter
from http://www.electronics-tutorials.ws/rc/rc_3.html
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
Differentiator and High Pass Filter
from http://www.electronics-tutorials.ws/rc/rc_3.html
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
Lab 9 Circuits

Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
Next Time: MSP 430, Bring Computer
and Install Code Composer
Dan O. Popa, Intro to EE, Freshman Practicum, Spring 2015
24