Download Unit_III

IMPEDANCE MATCHING IN HIGH FREQUENCY
LINES
UNIT - III
Impedance Matching
Maximum power is delivered when the load is matched the line and the power loss
in the feed line is minimized
Impedance matching sensitive receiver components improves the signal to noise
ratio of the system
Impedance matching in a power distribution network will reduce amplitude and
phase errors
Complexity
Bandwidth
Implementation
Adjustability
5/23/2017
2
Half and Quarter wave transmission lines
• The relationship of the input impedance at the
input of the half-wave transmission line with its
terminating impedance is got by letting L =
wavelength/2 in the impedance equation.
Zinput = ZL
• The relationship of the input impedance at the
input of the quarter-wave transmission line with
its terminating impedance is got by letting L
=wavelength/4 in the impedance equation.
Zinput = (Zinput Zoutput)0.5
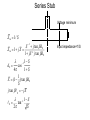
Series Stub
Voltage minimum
Z in  1 / S
S 1  j tan d 0
Z in  1  jX 
1  jS 1 j tan d 0

1 1  S
d0 
cos
4
1 S
1
X  (1  ) tan d 0
S
j tan  0   jX

1 1  S
0 
tan
2
S
Input impedance=1/S
Single Stub Tunning
Shunt Stub
G=Y0=1/Z0
Series Stub
5/23/2017
ELCT564
5
Single Shunt Stub Tuner Design Procedure
1. Locate normalized load impedance and draw VSWR circle (normalized load
admittance point is 180o from the normalized impedance point).
2. From the normalized load admittance point, rotate CW (toward generator) on
the VSWR circle until it intersects the r = 1 circle. This rotation distance is the
length d of the terminated section of t-tline. The nomalized admittance at this
point is 1 + jb.
3. Beginning at the stub end (rightmost Smith chart point is the admittance of
a short-circuit, leftmost Smith chart point is the admittance of an open-circuit),
rotate CW (toward generator) until the point at 0 - jb is reached. This rotation
distance is the stub length l.
5/23/2017
ELCT564
6
Smith Chart
• Impedances, voltages, currents, etc. all repeat
every half wavelength
• The magnitude of the reflection coefficient, the
standing wave ratio (SWR) do not change, so
they characterize the voltage & current patterns
on the line
• If the load impedance is normalized by the
characteristic impedance of the line, the
voltages, currents, impedances, etc. all still have
the same properties, but the results can be
generalized to any line with the same
normalized impedances
Smith Chart
• The Smith Chart is a clever tool for analyzing
transmission lines
• The outside of the chart shows location on the
line in wavelengths
• The combination of intersecting circles inside the
chart allow us to locate the normalized
impedance and then to find the impedance
anywhere on the line
Real Impedance
Axis
Smith Chart
Imaginary
Impedance Axis
Smith Chart
Constant Imaginary
Impedance Lines
Impedance
Z=R+jX
=100+j50
Normalized
z=2+j for
Zo=50
Constant Real
Impedance
Circles
Smith Chart
•
Impedance divided by line impedance
(50 Ohms)
• Z1 = 100 + j50
• Z2 = 75 -j100
• Z3 = j200
• Z4 = 150
• Z5 = infinity (an open circuit)
• Z6 = 0 (a short circuit)
• Z7 = 50
• Z8 = 184 -j900
•
Then, normalize and plot. The points are
plotted as follows:
• z1 = 2 + j
• z2 = 1.5 -j2
• z3 = j4
• z4 = 3
• z5 = infinity
• z6 = 0
• z7 = 1
• z8 = 3.68 -j18S
Smith Chart
• Thus, the first step in analyzing a transmission line is to
locate the normalized load impedance on the chart
• Next, a circle is drawn that represents the reflection
coefficient or SWR. The center of the circle is the center
of the chart. The circle passes through the normalized
load impedance
• Any point on the line is found on this circle. Rotate
clockwise to move toward the generator (away from the
load)
• The distance moved on the line is indicated on the
outside of the chart in wavelengths
Toward
Generator
Away
From
Generator
Constant
Reflection
Coefficient Circle
Scale in
Wavelengths
Full Circle is One Half
Wavelength Since
Everything Repeats
Single-Stub Matching
Yin  1  jB
Load impedance
Input admittance=S
1 
Yin 
S
1 
If YL is real, then the reflection coefficien t is real
Let d 0 be the distance from the voltage - minimum point wher e
Yin  1  jB
d0 

S 1
cos 1
4
S 1

S
1
The stub length  0 
tan
2
S 1
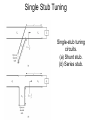
Single Stub Tuning
Single-stub tuning
circuits.
(a) Shunt stub.
(b) Series stub.
• 2 adjustable parameters
• d: from the load to the stub position.
• B or X provided by the shunt or series stub.
• For the shunt-stub case,
• Select d so that Y seen looking into the line at
d from the load is Y0+jB
• Then the stub susceptance is chosen as –jB.
• For the series-stub case,
• Select d so that Z seen looking into the line at
d from the load is Z0+jX
• Then the stub reactance is chosen as –jX.
Shunt Stubs
• Single-Stub Shunt Tuning
ZL=60-j80
.
(b) The two shunt-stub tuning solutions. (c)
Reflection coefficient magnitudes versus frequency
for the tuning circuits of (b).
• To derive formulas for d and l, let ZL= 1/YL= RL+
( RL  jX L )  jZ 0 tan  d
jXL.
Z Z
0
Y  G  jB 
Z 0  j ( RL  jX L ) tan  d
1
Z
RL (1  tan 2  d )
where G  2
RL  ( X L  Z 0 tan  d ) 2
•
RL2 tan  d  ( Z 0  X L tan  d )( X L  Z 0 tan  d )
B
Z 0 [ RL2  ( so
X L that
Z 0 tanG =
d ) 2Y] 0=1/Z0,
Now d is chosen
Z 0 ( RL  Z 0 ) tan 2  d  2 X L Z 0 tan  d  ( RL Z 0  RL2  X L2 )  0
X L  RL [( Z 0  RL ) 2  X L2 ]/ Z 0
tan  d 
, for RL  Z 0
RL  Z 0
• If RL = Z0, then tanβd = -XL/2Z0. 2 principal
solutions are



1

d  2

 1
 2

XL
XL
tan  
0
 for 2Z 0
 2Z 0 
1

XL 
XL
1 
0
   tan  
  for 2Z0
 2Z 0  

• To find the required stub length, BS = -B.
for open stub
1
1
1  BS 
1  B 

tan    
tan  
 2
2
 Y0 
 Y0 
l0
for short stub
1
1
1  Y0 
1  Y0 

tan   
tan  

2
B
 BS  2
l0
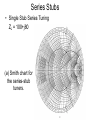
Series Stubs
• Single Stub Series Tuning
ZL = 100+j80
(a) Smith chart for
the series-stub
tuners.
(b) The two seriesstub tuning
solutions. (c)
Reflection
coefficient
magnitudes versus
frequency for the
tuning circuits of (b).
• To derive formulas for d and l, let YL= 1/ZL= GL+
(GL  jBL )  jY0 tan  d
jBL.
Y Y
0
Z  R  jX 
Y0  j (GL  jBL ) tan  d
1
Y
GL (1  tan 2  d )
where R  2
GL  ( BL  Y0 tan  d ) 2
•
GL2 tan  d  (Y0  BL tan  d )( BL  Y0 tan  d )
X
Y0 [GL2  (so
BL that
Y0 tanR d=) 2Z] 0=1/Y0,
Now d is chosen
Y0 (GL  Y0 ) tan 2  d  2 BLY0 tan  d  (GLY0  GL2  BL2 )  0
BL  GL [(Y0  GL ) 2  BL2 ]/ Y0
tan  d 
, for GL  Y0
GL  Y0
• If GL = Y0, then tanβd = -BL/2Y0. 2 principal
solutions are



1

d  2

 1
 2

BL
BL
tan  
0
 for 2Y0
 2Y0 
1

BL  
BL
1 
0
   tan  
  for 2Y0
 2Y0  

• To find the required stub length, XS = -X.
for short stub
1
1
1  X S 
1  X 

tan 
tan  

 2
2
 Z0 
 Z0 
l0
for open stub
1
1
1  Z 0 
1  Z 0 

tan 
tan  


2
X 
 X S  2
l0
Analytic Solution
• To the left of the first stub in Fig. 5.7b,
Y1 = GL + j(BL+B1) where YL = GL + jBL
• To the right of the 2nd stub,
GL  j ( BL  B1  Y0t )
Y2  Y0
where t  tan  d
Y0  jt (GL  jBL  jB1 )
• At this point, Re{Y2} = Y0
2
2
(
Y

B
t

B
t
)
1

t
L
1
GL2  GLY0 2  0
0
2
t
t
4t 2 (Y0  BL t  B1t ) 2
1 t2 
GL  Y0
1 1
2 
2t 
Y02 (1  t 2 ) 2



• Since GL is real,
4t 2 (Y0  BLt  B1t ) 2
0
1
2
2 2
Y0 (1  t )
Y0
1 t 2
0  GL  Y0 2  2
t
sin  d
• After d has been fixed, the 1st stub susceptance
can be determined as
Y0  (1  t 2 )GLY0  GL2t 2
B1   BL 
t
• The 2nd stub susceptance
can be found from the
negative of the imaginary part of (5.18)
2
2 2
• B2 = Y0 Y0GL (1  t )  GL t  GLY0
GLt
• The open-circuited stub length is
1
1  B 

tan  
 2
 Y0 
l0
• The short-circuited stub length is
1
1  Y0 

tan  

2
B
l0
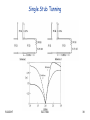
For a load impedance ZL=60-j80Ω, design two single-stub (short circuit) shunt
tunning networks to matching this load to a 50 Ω line. Assuming that the load is
matched at 2GHz and that load consists of a resistor and capacitor in series.
Single Stub Tunning
yL=0.3+j0.4
d1=0.176-0.065=0.110λ
d2=0.325-0.065=0.260λ
y1=1+j1.47
y2=1-j1.47
l1=0.095λ
l1=0.405λ
5/23/2017
ELCT564
29
Single Stub Tunning
5/23/2017
ELCT564
30
Results
For a load impedance ZL=25-j50Ω, design two single-stub (short circuit) shunt
tunning networks to matching this load to a 50 Ω line.
Single Stub tunning
yL=0.4+j0.8
d1=0.178-0.115=0.063λ
d2=0.325-0.065=0.260λ
y1=1+j1.67
y2=1-j1.6
l1=0.09λ
l1=0.41λ
5/23/2017
ELCT564
33
Single Series Stub Tuner Design Procedure
1. Locate normalized load impedance and draw VSWR circle
2. From the normalized load impedance point, rotate CW (toward generator) on
the VSWR circle until it intersects the r = 1 circle. This rotation distance is the
length d of the terminated section of t-tline. The nomalized impedance at this
point is 1 + jx.
3. Beginning at the stub end (leftmost Smith chart point is the impedance of a
short-circuit, rightmost Smith chart point is the impedance of an open-circuit),
rotate CW (toward generator) until the point at 0 ! jx is reached. This rotation
distance is the stub length l.
5/23/2017
ELCT564
34
For a load impedance ZL=100+j80Ω, design single series open-circuit stub
tunning networks to matching this load to a 50 Ω line. Assuming that the load is
matched at 2GHz and that load consists of a resistor and inductor in series.
Single Stub Tunning
zL=2+j1.6
d1=0.328-0.208=0.120λ
d2=0.5-0.208+0.172=0.463λ
z1=1-j1.33
z2=1+j1.33
l1=0.397λ
l1=0.103λ
5/23/2017
ELCT564
36
Single Stub Tunning
5/23/2017
ELCT564
37
Single Stub Tunning
5/23/2017
ELCT564
38
Double Stub Matching Network
a
b
jB2
b
jB1
YL
a

YL is transform ed into YL
YL  G L  jBL at the plane aa
The first stub adds a susceptanc e jB1 which moves the point
along constant conductanc e circle to P2
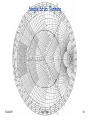
Double-Stub Tuning
• If an adjustable tuner was desired, single-tuner
would probably pose some difficulty.
Smith Chart Solution
• yL  add jb1 (on the rotated 1+jb circle)  rotate
by d thru SWR circle (WTG)  y1  add jb2 
Matched
• Avoid the forbidden region.
Double Stub Tunning
The susceptance of the first stub, b1, moves the load
admittance to y1, which lies on the rotated 1+jb circle; the
amount of rotation is de wavelengths toward the load. Then
transforming y1 toward the generator through a length d of
line to get point y2, which is on the 1+jb circle. The second
stub then adds a susceptance b2.
5/23/2017
ELCT564
41
Design a double-stub shunt tuner to match a load impedance ZL=60-j80 Ω to a 50 Ω
line. The stubs are to be open-circuited stubs and are spaced λ/8 apart. Assuming
that this load consists of a series resistor and capacitor and that the match frequency
is 2GHz, plot the reflection coefficient magnitude versus frequency from 1 to 3GHz.
Double Stub Tunning
yL=0.3+j0.4
b1=1.314
b1 =-0.114
’
y2=1-j3.38
l1=0.46λ
l2=0.204λ
5/23/2017
ELCT564
43
Double Stub Tunning
5/23/2017
ELCT564
45
Double-stub
tuning.
(a) Original
circuit with the
load an
arbitrary
distance from
the first stub.
(b) Equivalentcircuit with load
at the first stub.
Smith chart
diagram for the
operation of a
double-stub
tuner.
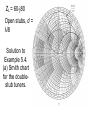
ZL = 60-j80
Open stubs, d =
λ/8
Solution to
Example 5.4.
(a) Smith chart
for the doublestub tuners.
(b) The two double-stub tuning solutions.
(c) Reflection coefficient magnitudes versus
frequency for the tuning circuits of (b).
x=1
YL
Pshort
circuit
Smith Chart
r=1
r=0.5
0
Popen
circuit
Real part of
Refl. Coeff.
x=-1
Move from P2 to P3 along a constant radius circle through an angle
  2 d
At the plane b - b the input admittance is Yb  Gb  jBb .
The P3 must lie on the G  1 circle. The stub will cancel jBb .
x=1
P2
YL
G1=1
Pshort
circuit
Popen
r=1
r=0.5
circuit
0
P3
Smith Chart
Real part of
Refl. Coeff.
x=-1
Rotate the the G=1 circle through an
angle -
The intersection of G=1 and the GL circle
determine the point P2
x=1
YL
Pshort
circuit
r=1
r=0.5
0
Popen
circuit
Real part of
Refl. Coeff.
x=-1
Smith Chart
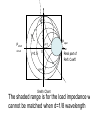
The shaded range is for the load impedance w
cannot be matched when d=1/8 wavelength
5/23/2017
ELCT564
53