* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download PowerPoint 演示文稿 - Sun Yat
Switched-mode power supply wikipedia , lookup
Stray voltage wikipedia , lookup
Buck converter wikipedia , lookup
Electrical substation wikipedia , lookup
Signal-flow graph wikipedia , lookup
Mains electricity wikipedia , lookup
Alternating current wikipedia , lookup
Electronic engineering wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Current source wikipedia , lookup
Topology (electrical circuits) wikipedia , lookup
Opto-isolator wikipedia , lookup
Integrated circuit wikipedia , lookup
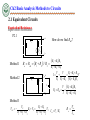
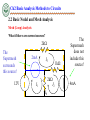
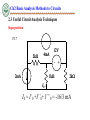
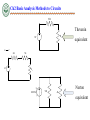
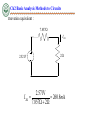
Engineering Circuit Analysis Ch2 Basic Analysis Methods to Circuits 2.1 Equivalent Circuits 2.2 Basic Nodal and Mesh Analysis 2.3 Useful Circuit Analysis Techniques References: Hayt-Ch3, 4; Gao-Ch2; Ch2 Basic Analysis Methods to Circuits 2.1 Equivalent Circuits Key Words: Equivalent Circuits Network Equivalent Resistance, Equivalent Independent Sources Ch2 Basic Analysis Methods to Circuits 2.1 Equivalent Circuits Equivalent Circuits Network о о Two-terminal Circuits Network cо о d о о a о 5 6 15 о 5 bо о I I a о + a о N1 + V V _ о о b b N2 Ch2 Basic Analysis Methods to Circuits 2.1 Equivalent Circuits Equivalent Resistance How do we find I1 and I2? I I1 I2 R1 R2 1 1 1 R1 R2 V R2 I R1 R1 R2 V R1 I2 I R2 R1 R2 I1 V - V I I1 + I2 = I + I I 1 1 V V V R1 R2 R1 R2 R1R2 R1 R2 Req I R1 R2 R1 R2 V V R1 R2 Req R1 R2 Ch2 Basic Analysis Methods to Circuits 2.1 Equivalent Circuits Equivalent Resistance i(t) i(t) + v(t) - + v(t) Req - Req is equivalent to the resistor network on the left in the sense that they have the same i-v characteristics. Ch2 Basic Analysis Methods to Circuits 2.1 Equivalent Circuits Equivalent Resistance Condition : without knowing V&I . We only know Rs Series and parallel Resistance Method 1 n 1 1 = R eqp k 1 R k n Reqs Rk K 1 (source-free) n G Gk k 1 Condition : without knowing Rs . We only know V&I a Method 2 I source V -free b Method 3 V Ro oc I sc Ro Rab V I source Voc source Isc Ch2 Basic Analysis Methods to Circuits 2.1 Equivalent Circuits Equivalent Resistance In practice , Vs-source voltage ≠ VL- Local VL Vs I L R Let Vs 10V;R 0.1 The IL-VL curve : VL 0, RL 0 , Short Circuit (SC) . I SC 100A IL(A) 100 0 10 VL 0, RL , Open Circuit (OC) . VOC 10V VOC R 0.1 O VL(V) I SC Ch2 Basic Analysis Methods to Circuits 2.1 Equivalent Circuits Equivalent Resistance P2.1 R2 R1 How do we find Rab? a R3 + - VS Method 1 b Ro Rab R1 R2 // R3 I Method 2 R2 R1 R1 R2 R3 R1 R2 R3 I a R3 V V R R R 1 2 3V R3 R1 R2 R1 R2 R3 V Ro Rab b V R1 R2 R3 I R1 R2 R3 Method 3 VoC VS R1 R2 R3 VS VS I V / R sc s 3 R1 R2 R3 R1 R2 R3 Ro Voc I sc Ch2 Basic Analysis Methods to Circuits 2.1 Equivalent Circuits Source Transformation • Ideally: – An ideal current source has the voltage necessary to provide its rated current – An ideal voltage source supplies the current necessary to provide its rated voltage • Practice: – A real voltage source cannot supply arbitrarily large amounts of current – A real current source cannot have an arbitrarily large terminal voltage Ch2 Basic Analysis Methods to Circuits 2.1 Equivalent Circuits Source Transformation Rs Vs + Is - Vs Rs I s Rs Is Vs Rs Note: Consistency between the current source ref. direction and the voltage source ref. terminals. Ch2 Basic Analysis Methods to Circuits 2.1 Equivalent Circuits Equivalent Source How do we find I1 and I2? Is1 Is2 R2 V I s1 I s 2 R1 R1 R2 R1 V I s1 I s 2 R2 R1 R2 I1 I2 + I1 R1 R2 V I2 - I1 I 2 I s1 I s 2 1 1 V V I s1 I s 2 V R1 R2 R1 R2 V I s1 I s 2 Ieq R1 R2 R1 R2 Ch2 Basic Analysis Methods to Circuits 2.1 Equivalent Circuits Equivalent Source Series Voltage Source n + VS1 - + VS2 - + VSn - + VS VS VSk k 1 - n R S R Sk k 1 parallel Current Source IS1 IS2 ISn I RS=RS1// RS2//…// RSn IS n I S I Sk k 1 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Key Words: Branch Analysis, Nodal Analysis, Mesh (Loop) Analysis • Why? – The previous analytical techniques (voltage divider, equivalent resistance, etc.) provide an intuitive approach to analyze circuits – They are not systematic and cannot be easily automated by a computer • Comments: – Analysis of circuits using node or loop analysis requires solutions of systems of linear equations. – These equations can usually be written by inspection of the circuit. Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Branch Analysis P2.2 How do we find I1 and I2, I3? R3=80 R1=0.5 I1 I2 R2=0.4 + VS=14V _ KCL I3 E2=12V KVL Mesh 1: 14 0.5I1 0.4I 2 12 0 2 0.4 I 2 I1 4 0.8I 2 0.5 Mesh 2: 12 0.4I 2 80I3 0 I3 12 0.4 I 2 0.15 0.005I 2 80 4 0.8I 2 I 2 0.15 0.005I 2 I1 I 2 I 3 Vs E2 I 2 R2 2 0.4 I 2 E I R 12 0.4 I 2 I3 2 2 2 R3 80 R1 0.5 2 0.4 I 2 12 0.4 I 2 I2 I 2 2.14A I1 2.29A I 3 0.14A 0.5 80 I1 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Branch Analysis Suppose m branches, n nodals write KCL equation for each independent node. ——(n-1) KCL equations write KVL equation for each independent mesh/loop ——m-(n-1) KVL equations Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Branch Analysis Here’s a quick example of a circuit that we will see later when we model the operation of transistors. For now, let’s assume ideal independent and dependent sources. Ⅰ We can write the following equations: Ⅰ: Ⅱ: Ⅱ Ⅲ Ⅲ: i1 iC iCC 0 iB i2 i1 0 iE iB iC 0 iC iB Vo iE RE i2 R2 0 VCC i1R1 i2 R2 0 iB Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Nodal Analysis 1) Choose a reference node 500 500 + I1 500 1k V 500 - The reference node is called the ground node. I2 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Nodal Analysis 1) Choose a reference node 500 . Ⅰ I4 I5 I1 500 .I 500 Ⅱ + I8 6 1k V - 0 KCL Ⅰ: Ⅱ: Ⅲ: . I7 Ⅲ 500 I2 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Nodal Analysis 2) Assign node voltages to the other nodes 500 V1 I 4 1 I1 I5 V2 2 500 I6 I8 1k 500 I 7 V3 3 500 0 V1, V2, and V3 are unknowns for which we solve using KCL. I2 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Nodal Analysis 3) Apply KCL to each node except the reference node and express currents in terms of the node voltages. V1 I4 500 V2 500 I7 V3 1 I5 I1 2 I6 I8 1k 500 3 500 0 KCL • • • Node ① : I 4 I5 I1 0 Node ② : I 6 I 4 I 7 0 Node ③ : I8 I 7 I 2 0 V1 V1 V2 I 5 500 500 , V V V I6 2 , I7 3 2 1K 500 I4 , , I8 V3 500 V1 V2 V 1 0 500 500 V V1 V2 V2 V3 Node ② : 2 0 500 1k 500 V3 V2 V 3 I2 0 Node ③ : 500 500 Node ① : I1 I2 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Nodal Analysis 4) Solve the resulting system of linear equations. • Node 1: 1 V 1 V1 2 I1 500 500 500 • Node 2: • Node 3: • • V1 1 1 V 1 V2 3 0 500 500 1k 500 500 V2 1 1 V3 I2 500 500 500 V1 500 I1 1 V2 500 V3 2 500 3 1k 500 0 The left hand side of the equation: – The node voltage is multiplied by the sum of conductances of all resistors connected to the node. – The neighboring node voltages are multiplied by the conductance of the resistor(s) connecting to the two nodes and to be subtracted. The right hand side of the equation: – The sum of source currents entering the node directly. I2 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Nodal Analysis 4) Solve the resulting system of linear equations. • Node 1: 1 V 1 V1 2 I1 500 500 500 • Node 2: • Node 3: V1 1 1 V 1 V2 3 0 500 500 1k 500 500 V1 500 I1 1 V2 500 V3 2 500 V2 1 1 V3 I2 500 500 500 3 1k Matrix Notation(Symmetric) 1 1 500 500 1 500 0 1 500 1 1 1 500 1k 500 1 500 V 1 I1 1 V2 0 500 1 1 V3 I 2 500 500 0 500 I2 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Nodal Analysis 4) Solve the resulting system of linear equations. • Node 1: • Node 2: • Node 3: 1 V 1 V1 2 I1 500 500 500 V1 1 1 V 1 V2 3 0 500 500 1k 500 500 V1 500 I1 1 V2 1 1 V3 I2 500 500 500 G11V1+G12V2 +G13V3 =I11 G21V2+G22V2 +G23V3 =I22 G31V1+G32V2+G33V3=I33 V2 500 V3 2 500 3 1k 500 I2 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Nodal Analysis What if there are dependent sources? Example: V1 Ib 1 5mA 1k V2 50 100Ib 2 1k + Vo V V1 V2 5mA 1k 50 Node ①: 1 1 1 1k 50 1 100 50 50 V V1 V 100 I b 2 0 50 1k Node ② :2 1 V1 5mA 50 1 100 1 V2 0 50 50 1k Ib V1 V2 50 V2 V1 V V V 100 1 2 2 0 50 50 1k Matrix is not symmetric due to the dependent source. Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Nodal Analysis What if there are voltage sources? 0.7V R1 I b V2 1k 2 1 V1 Node 2: Node 3: + - + 3k - V3 3 V4 R3 50 + 4 100Ib R2 R4 Vo 1k - V2 V1 V2 I b 0 Difficulty: We do not know I – the current b 1k 3k through the voltage source. V3 V4 Ib 0 V3 V4 V4 50 100 I b 0 Node 4: 50 1k Independent Voltage Source: V3 V2 0.7V Equations: KCL at node 2, node 3, node 4, and V3 V2 0.7V Unknowns: Ib, V2 (V3),V4 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Nodal Analysis What if there are voltage sources? CURRENT CONTROLLED VOLTAGE SOURCE Io=? V2 V1 2kIx V1 2kI x V2 2V1 KCL AT SUPERNODE Ix V1 V2 - 4mA + + 2mA + = 0 2k 2k V1 2k V1 V2 4(V ) 3V2 8(V ) IO V2 4 mA 2k 3 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Nodal Analysis Advantages of Nodal Analysis • • • • • Solves directly for node voltages. Current sources are easy. Voltage sources are either very easy or somewhat difficult. Works best for circuits with few nodes. Works for any circuit. Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Mesh(Loop) Analysis 1) Identifying the Meshes 1k V1 1k + - + Mesh 1 Mesh 2 - V2 1k Mesh: A special kind of loop that doesn’t contain any loops within it. Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Mesh(Loop) Analysis 2) Assigning Mesh Currents 1k V1 1k + - 1k I1 + I2 - V2 3) Apply KVL around each loop to get an equation in terms of the loop currents. I1 ( 1k + 1k) - I2 1k = V1 For Mesh 1: -V1 + I1 1k + (I1 - I2) 1k = 0 For Mesh 2: (I2 - I1) 1k + I2 1k + V2 = 0 - I1 1k + I2 ( 1k + 1k) = -V2 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Mesh(Loop) Analysis 3) Apply KVL around each loop to get an equation in terms of the loop currents. 1k I1 ( 1k + 1k) - I2 1k = V1 - I1 1k + I2 ( 1k + 1k) = -V2 V1 + - 1k 1k I1 4) Solve the resulting system of linear equations. 1k I1 V1 1k 1k 1k I V 1 k 1 k 2 2 I2 + - V2 Ch2 Basic Analysis Methods to Circuits + 5 5 2.2 Basic Nodal and Mesh Analysis I1 US _ I1 5 MeshI (Loop) I I Analysis I I 1 1 1 1 1 5 I1 R11I m1 R12 I m 2 R13 I m 3 VS 11 R21I m1 R22 I m 2 R23 I m 3 VS 22 I E I1 S R31I m1 R32 I m 2 R33 I m 3 VS 33 I3 Mesh 1: I m1R1 VS1 I m1 I m3 R6 VS 2 I m1 I m 2 R2 0 R3 Mesh 2: I m 2 R3 VS 3 I m 2 I m3 R5 VS 2 I m1 I m 2 R2 0 Mesh 3: I m 2 I m3 R5 I m3 I m1 R6 I m3 R4 VS 4 0 I2 _ VS1 + R1 Im1 Mesh 1 R2 + VS2 Mesh 2 Im2 _ + _ VS3 I6 I5 R5 R6 Mesh 3 R 4 I4 Im3 _ + VS4 ( R1 R2 R6 ) I m1 R2 I m 2 R6 I m 3 VS 1 VS 2 R2 I m1 ( R2 R3 R5 ) I m 2 R5 I m 3 VS 2 VS 3 R6 I m1 R5 I m 2 ( R4 R5 R6 ) I m 3 VS 4 R2 R6 R1 R2 R6 I m1 VS1 VS 2 I V V R R R R R 2 2 3 5 5 m2 S 2 S 3 R6 R5 R4 R5 R6 I m3 VS 4 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Mesh (Loop) Analysis R11I m1 R12 I m 2 R13 I m3 VS11 R21I m1 R22 I m 2 R23 I m3 VS 22 R31I m1 R32 I m 2 R33 I m3 VS 33 P2.4(P2.2) R3=80 R1=0.5 + VS=14V _ Mesh 1: R1 R2 I m1 R2 I m2 VS 12 R2=0.4 Im2 Im1 E2=12V VS I m1R1 I m1 I m 2 R2 12 0 Mesh 2: 12 I m 2 I m1 R2 I m 2 R3 0 I m1 R2 R2 R3 I m 2 12 R1 R2 R2 I m1 VS 12 R -12 R R I 12 2 3 m2 2 2 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Mesh (Loop) Analysis What if there are current sources? I1 US I1 P2.5 I1 I1 I1 + 40V _ • The current sources in this circuit will have whatever voltage is necessary to make the current correct. • We can’t use KVL around the loop because we don’t know the R 1 R1 P2.6 _ voltage. Mesh 1 1 2 I=? I I20 1 I1 R1 50 R1 I1 I Im1 30 m2 2A Im2 + 7V _ + V Im1 - 3 2A Mesh 2 Im3 40 I m1 20 I m1 I m 2 30 0 I m 2 2A I I m1 I m 2 I m1 = Super Mesh: 7 I m 2 2 I m3 1 0 Mesh 2: 1 I m1 I m3 2 2 Super Mesh Mesh 1: Im2 Im1 1 Im2 2 Im2 Im3 3 0 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Mesh (Loop) Analysis What if there are current sources? 2k The Supermesh surrounds this source! 2mA I3 + 12V - 2k I2 I1 I0 1k The Supermesh does not include this source! 4mA Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Mesh (Loop) Analysis What if there are current sources? 2k • The 4mA current source sets I2: 2mA I3 I2 = -4mA 1k • The 2mA current source sets a constraint on I1 and I3: 2k + 12V 4mA I2 I1 I1 - I3 = 2mA I0 • We have two equations and three unknowns. Where is the third equation? - 12 2k I 3 1k I 3 I 2 2k I1 I 2 0 I1 2k I 2 1k 2k I 3 1k 2k 12V I 2 4mA ; I 3 0.8mA ; I1 1.2mA Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Mesh (Loop) Analysis What if there are current sources? P2.6 + 7V _ Mesh 1 1 + V Im1 - 2 Im2 Mesh 2: -7V+I m 2 2 I m3 1 0 3 Node 3: I m1 I m3 2A 2A Im3 2 Node 3 Mesh 2 Mesh 1: -7V+ I m1 I m2 1 I m3 I m2 3 I m3 1 0 1 Ch2 Basic Analysis Methods to Circuits 2.2 Useful Circuit Analysis Techniques Mesh(Loop) Analysis Dependent current source. Current sources not shared by meshes. We treat the dependent source as a conventional source. Equations for meshes with current sources We are asked for Vo. We only need to solve for I3 . Replace and rearrange Then KVL on the remaining loop(s) Vx 2kI1 I1 2 I 2 4mA Vx 4k ( I1 I 2 ) 8kI3 = 3 + 2kI1 ⇒I 3 = And express the controlling variable, Vx, in terms of loop currents VO 6kI 3 33 [V ] 4 11 mA 8 Ch2 Basic Analysis Methods to Circuits 2.2 Basic Nodal and Mesh Analysis Mesh (Loop) Analysis Advantages of Loop Analysis • • • • Solves directly for some currents. Voltage sources are easy. Current sources are either very easy or somewhat difficult. Works best for circuits with few loops. Disadvantages of Loop Analysis • Some currents must be computed from loop currents. • Choosing the supermesh may be difficult. Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Key Words: Linearity Superposition Thevenin’s and Norton’s theorems Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Linearity • Linearity is a mathematical property of circuits that makes very powerful analysis techniques possible. • Linearity leads to many useful properties of circuits: – Superposition: the effect of each source can be considered separately. – Equivalent circuits: Any linear network can be represented by an equivalent source and resistance (Thevenin’s and Norton’s theorems) Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Linearity • Linearity leads to simple solutions: – Nodal analysis for linear circuits results in systems of linear equations that can be solved by matrices V1 500 1 I1 500 V3 2 500 1 1 500 500 1 500 0 V2 3 1k 1 500 1 1 1 500 1k 500 1 500 500 V I 1 1 1 V2 0 500 1 1 V3 I 2 500 500 0 I2 Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Linearity • The relationship between current and voltage for a linear element satisfies two properties: – Homogeneity – Additivity *Real circuit elements are not linear, but can be approximated as linear Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Linearity • Homogeneity: – Let v(t) be the voltage across an element with current i(t) flowing through it. – In an element satisfying homogeneity, if the current is increased by a factor of K, the voltage increases by a factor of K. • Additivity – Let v1(t) be the voltage across an element with current i1(t) flowing through it, and let v2(t) be the voltage across an element with current i2 (t) flowing through it – In an element satisfying additivity, if the current is the sum of i1 (t) and i2 (t), then the voltage is the sum of v1 (t) and v2 (t). Example: Resistor: V = R I – If current is KI, then voltage is R KI = KV – If current is I1 + I2, then voltage is R(I1 + I2) = RI1 + RI2 = V1 + V2 Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques I1 Superposition US _ R1 R1 R3=80 I1 I1 I1 I1 I1 I1 I2 R1 R1 R3 R3 I2 VS E2 R R R1 R3 R2 R3 R R R2 R3 R1 R3 1 2 1 2 I R1 I1 I 2 I 2 S R1=0.5 + VS=14V _ I R2=0.4 E2=12V • Superposition is a direct consequence of linearity • It states that “in any linear circuit containing multiple independent sources, the current or voltage at any point in the circuit may be calculated as the algebraic sum of the individual contributions of each source acting alone.” Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Superposition How to Apply Superposition? • To find the contribution due to an individual independent source, zero out the other independent sources in the circuit. – Voltage source short circuit. – Current source open circuit. • Solve the resulting circuit using your favorite techniques. – Nodal analysis – Loop analysis Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Superposition For the above case: Zero out Vs, we have : Zero out E2, we have : I I2’’ R1 R3 I2’ R1 R2 E2 RR R1 / / R3 1 3 R1 R3 R R R2 R3 R1R3 R2 R1 / / R3 1 2 R1 R3 E2 R1 R3 I 2 R1 R2 R2 R3 R1R3 + Vs_ R3 R2 R2 / / R3 E2 R1 R1 / / R3 R2 R3 R2 R3 R1 R2 R2 R3 R1 R3 R2 R3 Vs R2 R3 I R1 R2 R2 R3 R1 R3 I 2 I R3 Vs R3 R2 R3 R1 R2 R2 R3 R1 R3 Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Superposition P2.7 2k 4mA 12V 2mA 1k I0 + 2k Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Superposition P2.7 I 0 I 2 I1 I1 2mA 2k KVL for mesh 2: I 2 I1 1k I 2 2k 0 2mA I1 1k Io ’ Mesh 2 I2 2k 1 2 I 2 I1 mA 3 3 2 I 0 I 2 I1 2 3 4 mA 3 Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Superposition P2.7 I 0 I 2 2k 4mA I1 I 2 1k I 2 I1 0 I 2 2k 0 1k I’’0 KVL for mesh 2: Mesh 2 I2 2k I2 0 I o 0 Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Superposition P2.7 I o I 2 12V 2k KVL for mesh 2: - 1k I’’’0 + I2 I 2 1k 12V I 2 2k 0 2k I2 12 4mA 1k 2k Mesh 2 I o 4mA Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Superposition P2.7 2k 4mA 12V - 2mA 1k + 2k I0 I0 = I’0 +I’’0+ I’’’0 = -16/3 mA Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Thevenin’s theorem • Any circuit with sources (dependent and/or independent) and resistors can be replaced by an equivalent circuit containing a single voltage source and a single resistor • Thevenin’s theorem implies that we can replace arbitrarily complicated networks with simple networks for purposes of analysis Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Thevenin’s theorem Independent Sources RTh Voc Circuit with independent sources + - Thevenin equivalent circuit Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Thevenin’s theorem No Independent Sources RTh Circuit without independent sources Thevenin equivalent circuit Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Norton’s theorem • Very similar to Thevenin’s theorem • It simply states that any circuit with sources (dependent and/or independent) and resistors can be replaced by an equivalent circuit containing a single current source and a single resistor Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Norton’s theorem Norton Equivalent: Independent Sources Isc Circuit with one or more independent sources RTh Norton equivalent circuit Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Norton’s theorem Norton Equivalent: No Independent Sources RTh Circuit without independent sources Norton equivalent circuit Ch2 Basic Analysis Methods to Circuits • Motivation of applying the Thevenin’s theorem and Norton’s theorem: – Sometimes, in a complex circuit, we are only interested in working out the voltage /current or power being consumed by a single load (resistor); – We can then treat the rest of the circuit (excluding the interested load) as a voltage (current) source concatenated with a source resistor; – Simplify our analysis. • The Thevenin’s theorem: – Given a linear circuit, rearrange it in the form of two networks of A and B connected by two wires. Define Voc as the open-circuit voltage which appears across the terminals of A when B is disconnected. Then all currents and voltage in B will remain unchanged, if we replace all the independent current or voltage source in A by an independent voltage source which is in series with a resistor (RTh). • The Norton’s Theorem: – Given a linear circuit, rearrange it in the form of two networks of A and B connected by two wires. Define isc as the short-circuit current which appears across the terminals of A when B is disconnected. Then all currents and voltage in B will remain unchanged, if we replace all the independent current or voltage source in A by an independent current source isc which is in parallel with a resistor (RN). Ch2 Basic Analysis Methods to Circuits • Equivalent transform between a Thevenin equivalent circuit and a Norton equivalent circuit RTH vL VL vS If RL iS vL vL RL RN Thevenin equivalent Norton equivalent RL VvLL vS RL RTH RN VL is RL RL RTHN RTH RN and v VLL = vs is RN is RTH VvLL Ch2 Basic Analysis Methods to Circuits • Therefore, for a source transform: Thevenin Norton Norton: RN RTH , is vs / RTH Thevenin : RTH RN , vs is RN Ch2 Basic Analysis Methods to Circuits • Example 45 (P88) Find a Thevenin and Norton equivalent circuit for the following circuit excluding RL 3 7 12V 6 A T RL B N 7 7 4A 3 6 RL 4A 2 RL Ch2 Basic Analysis Methods to Circuits 9 Thevenin RL 8V N T 2 8V equivalent 7 RL 0.889A 9 RL Norton equivalent Ch2 Basic Analysis Methods to Circuits • Application of Thevenin’s theorem when there are only independent sources. step : 1) Determine v of two connection points between network A and network B. oc 2) Determine R of two connection points by replacing the voltage source by a shortTH circuit or the current source by a open-circuit. Test the above case? • Similarly, for Norton’s Theorem steps : 1) Determine iSC between the two connection points between network A and B. 2) Determine R by two connection points by replacing the voltage source by a shortN circuit or the current source by an open circuit. Ch2 Basic Analysis Methods to Circuits • Practice 4.6 (P90) 4 5 9V I 2 ? 2 4 6 5 4 9V 4 voc VS VOC 9V 4 2.571V 4 4 6 6 5 10 4 RTH 1 1 1 20 RTH ( ) 5 5 7.857 10 4 7 Ch2 Basic Analysis Methods to Circuits Thevenin equivalent : 7.857 I 2 2.521V 2 2.571V I 2 260.8mA 7.857 2 Ch2 Basic Analysis Methods to Circuits • When there are multiple independent source, we shall use “superposition” . Example 4.7 (P91) Find the Thevenin and Norton equivalent for the network excluding the 1k resistor. 2k 3k 4V To determine 2mA 1k voc, when only 4v voltage source is functioning. 5K 4V voc' voc' 4V Ch2 Basic Analysis Methods to Circuits When only 2mA current source is functioning : 5k 3k voc 2k N T 4V 2mA Therefore, vc voc v v 4V 4V 8V ' oc '' oc voc'' voc'' 4V Ch2 Basic Analysis Methods to Circuits To determine RTH 5k RTH 5k Thevenin equivalent: 5k RTH VS 8V 1k RN RTH 5k iS vs / RTH 1.6mA Ch2 Basic Analysis Methods to Circuits Norton equivalent vs 1.6mA RN 5k 1k Try to look into this problem from the Norton approach. (Figure out the Norton equivalent circuit first) Ch2 Basic Analysis Methods to Circuits When there are both independent source and dependent source. —Dependent source cannot be “zero out” as far as its controlling variable is not zero. —Similar as before, vs voc —But we cannot determine RTH ( RN ) directly, however, we can use RTH ( RN ) voc Example 4.8 (P92) — Determine the Thevenin equivalent of the following circuit 2k 4V To determine since voc voc vx 3k vx 4000 vx ,applying KVL to the supermesh: VX 4V ( ) 2k 3k 0 vx 0 4000 vs voc vx 8V / isc Ch2 Basic Analysis Methods to Circuits To determine isc 2k 3k vx 0 vx 0 4000 4V iSC 4V 0.8mA 5k RTH vOC / iSC 8V 10k 0.8mA Therefore its Thevenin equivalent is: RTH 10k vs 8V Ch2 Basic Analysis Methods to Circuits • When there are only dependent sources: – VOC = 0 – RTH can be determined by implying a test (imaginary) voltage across the two terminals. 3Ω i Example 4.9 (p93) Open circuit : i 0 , 1.5i 2 0 , VOC 0 2 3 1.5i To determine RTh, imagine an independent current source xA. as : i = -xA, v RTh = x Apply KCL: 3Ω 1.5( - x) - v v + + ( - x) = 0 3 2 i 1.5i 2Ω v xA v = 0.6x V RTh = 0.6Ω Giving : 0.6Ω 2Ω Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Thevenin’s theorem • Circuits with independent sources – Compute the open circuit voltage, this is Voc – Compute the Thevenin resistance (set the sources to zero – short circuit the voltage sources, open circuit the current sources), and find the equivalent resistance, this is RTh • Circuits with independent and dependent sources: – Compute the open circuit voltage – Compute the short circuit current – The ratio of the two is RTh • Circuits with dependent sources only* – Voc is simply 0 – RTh is found by applying an independent voltage source (V volts) to the terminals and finding voltage/current ratio * Not required by this course. Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Norton’s theorem • Circuits with independent sources, w/o dependent sources – Compute the short circuit current, this is Isc – Compute the Thevenin resistance (set the sources to zero – short circuit the voltage sources, open circuit the current sources), and find the equivalent resistance, this is RN • Circuits with both independent and dependent sources – Find Voc and Isc – Compute RN= Voc/ Isc • Circuits w/o independent sources* – Apply a test voltage (current) source – Find resulting current (voltage) – Compute RN Ch2 Basic Analysis Methods to Circuits 2.3 Useful Circuit Analysis Techniques Maximum power transfer VL2 RL PL ; VL VTH RL RTH RL RTH + - VTH VL RL (LOAD) SOURCE RTH RL 2RL 0 PL RL V2 2 TH RTH RL For every choice of RL we have a different power. How do we find the maximum value? Consider PL as a function of RL and find the maximum of such function 2 dPL R R 2 RL RTH RL 2 TH L VTH 4 dRL RTH RL RL* RTH The maximum power transfer theorem The load that maximizes the power transfer for a circuit is equal to the Thevenin equivalent resistance of the circuit. The value of the maximum power that can be transferred is 2 VTH PL (max) 4 RTH Ch2 Basic Analysis Methods to Circuits Analysis methods Review KVL, KCL, I — V Combination rules Node method Mesh method Superposition Thévenin Norton Any circuits linear circuits