* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download EEE 302 Lecture 23 - Arizona State University
Resistive opto-isolator wikipedia , lookup
Amateur radio repeater wikipedia , lookup
405-line television system wikipedia , lookup
Atomic clock wikipedia , lookup
Waveguide filter wikipedia , lookup
Loudspeaker wikipedia , lookup
Spectrum analyzer wikipedia , lookup
Wien bridge oscillator wikipedia , lookup
Regenerative circuit wikipedia , lookup
Valve RF amplifier wikipedia , lookup
Mechanical filter wikipedia , lookup
Phase-locked loop wikipedia , lookup
Index of electronics articles wikipedia , lookup
Superheterodyne receiver wikipedia , lookup
Audio crossover wikipedia , lookup
Radio transmitter design wikipedia , lookup
Linear filter wikipedia , lookup
Analogue filter wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
RLC circuit wikipedia , lookup
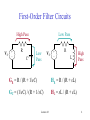
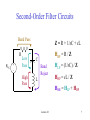
EEE 302 Electrical Networks II Dr. Keith E. Holbert Summer 2001 Lecture 23 1 Filter Networks • Filters pass, reject, and attenuate signals at various frequencies • Common types of filters: Low-pass: pass low frequencies and reject high frequencies High-pass: pass high frequencies and reject low frequencies Band-pass: pass some particular range of frequencies, reject other frequencies outside that band Band-rejection: reject a range of frequencies and pass all other frequencies (e.g., a special case is a notch filter) Lecture 23 2 Common Filter Bode Plots Low Pass High Pass Frequency Frequency Band Reject Band Pass Frequency Frequency Lecture 23 3 Passive Filters • Passive filters use R, L, C elements to achieve the desired filter • The half-power frequency is the same as the break frequency (or corner frequency) and is located at the frequency where the magnitude is 1/2 of its maximum value • The resonance frequency, 0, is also referred to as the center frequency • We will need active filters to achieve a gain greater than unity Lecture 23 4 Class Examples • Extension Exercise E12.16 • Extension Exercise E12.17 • Extension Exercise E12.18 Lecture 23 5 First-Order Filter Circuits High Pass VS + – R C Low Pass Low Pass VS + – R L GR = R / (R + 1/sC) HR = R / (R + sL) GC = (1/sC) / (R + 1/sC) HL = sL / (R + sL) Lecture 23 High Pass 6 Second-Order Filter Circuits Band Pass R VS + – Low Pass High Pass Z = R + 1/sC + sL HBP = R / Z C Band Reject L HLP = (1/sC) / Z HHP = sL / Z HBR = HLP + HHP Lecture 23 7 Frequency & Time Domain Connections • First order circuit break frequency: break = 1/ • Second order circuit characteristic equation s2 + 20 s + 02 [ = 1/(2Q) ] (j)2 + 2(j) + 1 [ = 1/0 ] s2 + BW s + 02 s2 + R/L s + 1/(LC) [series RLC] Q value also determines damping and pole types Q < ½ ( > 1) overdamped, real & unequal roots Q = ½ ( = 1) critically damped, real & equal roots Q > ½ ( < 1) underdamped, complex conjugate pair Lecture 23 8 PSpice Design Example • Repeat E12.18 using Pspice – Plot the resistor voltage in DBs – Use goal function “BPBW” to determine the band-pass filter bandwidth: BPBW(VDB(#),3)) – Use goal function “CenterFreq(VDB(#),0?)” • Bandwidth design – Design circuit to achieve a bandwidth of 300 Hz • Center frequency design – Design circuit for a center frequency of 100 Hz Lecture 23 9