* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 5
Power factor wikipedia , lookup
Ground (electricity) wikipedia , lookup
Electric power system wikipedia , lookup
Audio power wikipedia , lookup
Three-phase electric power wikipedia , lookup
Electrification wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Power inverter wikipedia , lookup
Wireless power transfer wikipedia , lookup
Spectral density wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Current source wikipedia , lookup
Electrical ballast wikipedia , lookup
Power MOSFET wikipedia , lookup
Regenerative circuit wikipedia , lookup
Spark-gap transmitter wikipedia , lookup
Utility frequency wikipedia , lookup
Stray voltage wikipedia , lookup
Electrical substation wikipedia , lookup
Power engineering wikipedia , lookup
Power electronics wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Amtrak's 25 Hz traction power system wikipedia , lookup
History of electric power transmission wikipedia , lookup
Surge protector wikipedia , lookup
Voltage optimisation wikipedia , lookup
Opto-isolator wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Buck converter wikipedia , lookup
Mains electricity wikipedia , lookup
Alternating current wikipedia , lookup
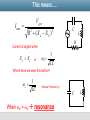
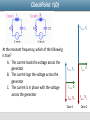
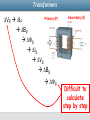
Physics 2112 Unit 21 Outline: Resonance Power/Power Factor Q factor What is means A useful approximation Transformers From last time….. “Ohms Law” for each element Vresistor I max R Vinductor I max X L Vcapacitor I max X C C I max Vgen L R Z Vgen I max Z Z R 2 X L X C 2 (impedance) where: X L L 1 XC C of generator XL (inductive reactance) (capacitive reactance) R XC This means….. I max Vgen R (X L XC ) 2 2 C L R Current is largest when X L XC or d 1 LC Where have we seen this before? o 1 LC (Natural Frequency) When d = o resonance C L Resonance Frequency at which voltage across inductor and capacitor cancel R is independent of Resonance in AC Circuits XL increases with XC increases with 1/ 1 XC C Z R ( X L XC ) 2 Z = R at resonance Impedance X L L Z 2 XL 0 is minimum at resonance Resonance: XL XC 0 1 LC XC frequency R Example 21.1 (Tuning Radio) A radio antenna is hooked to signal filter consisting of a resistor, a variable capacitor and a 50uH inductor. If we would like to get maximum current for the signal from our favorite country music station, US 99 (99.5MHz), what should we set the capacitor to? C L R amplifier Example 21.2 (Peak Current) C A generator with peak voltage 15 volts and angular frequency 25 rad/sec is connected in series with an 8 Henry inductor, a 0.4 mF capacitor and a 50 ohm resistor. What is the peak current through the circuit? R L CheckPoint 1(A) Imax XL Consider two RLC circuits with identical generators and resistors. Both circuits are driven at the resonant frequency. Circuit II has twice the inductance and 1/2 the capacitance of circuit I as shown above. Compare the peak voltage across the resistor in the two circuits. A. VI > VII Resonance: XL XC B. VI = VII Z R C. VI < VII Same since R doesn't change Imax XL Imax R Imax R Imax XC Case 1 Imax XC Case 2 CheckPoint 1(B) Imax XL Consider two RLC circuits with identical generators and resistors. Both circuits are driven at the resonant frequency. Circuit II has twice the inductance and 1/2 the capacitance of circuit I as shown above. Compare the peak voltage across the inductor in the two circuits A. VI > VII Voltage in second circuit will B. VI = VII be twice that of the first because of the 2L compared C. VI < VII to L. Imax XL Imax R Imax R Imax XC Case 1 Imax XC Case 2 CheckPoint 1(C) Imax XL Consider two RLC circuits with identical generators and resistors. Both circuits are driven at the resonant frequency. Circuit II has twice the inductance and 1/2 the capacitance of circuit I as shown above. Compare the peak voltage across the capacitor in the two circuits A. VI > VII B. VI = VII The peak voltage will be C. VI < VII greater in circuit 2 because the value of XC doubles. Imax XL Imax R Imax R Imax XC Case 1 Imax XC Case 2 CheckPoint 1(D) Imax XL At the resonant frequency, which of the following is true? A. The current leads the voltage across the generator B. The current lags the voltage across the generator C. The current is in phase with the voltage across the generator Imax XL Imax R Imax R Imax XC Case 1 Imax XC Case 2 Resonance….what it means….. A circuit is in resonance when…. “ frequency of the signal generator is the same as the natural frequency of the circuit. Imax = e/R Voltage drop across the resistor is maximum XL = XC Z has minimum value phase angle, f, is zero voltage and current are in sync at the signal generator. Power What is the power put into circuit by signal? C At any instant P=VI varies with time. But V and I not in sync at genarator R L Power PIN = POUT RMS Root Mean Square I rms I peak / 2 PAVG I 2 rms I rms R R (I 2 peak Vrms V R rms Z cos f PAVG I rmsV rmscos f / 2) R C L R Changes electrical energy into thermal energy Example 21.3 (Power lost) How much electrical energy was turned into thermal energy every minute in the three situations we had in example 20.2? Recall =60rad/sec =400rad/sec =206rad/sec f =-72o f=55.7o f = 0o In the circuit to the right • L=500mH • Vmax = 6V • C=47uF • R=100W Example 21.4 A bright electric light bulb and a small window air conditioner both are plugged into a wall socket with puts out Vrms=120V. Both draw Irms= 1amp of current. The light bulb has a power factor of 1 and the AC unit has a power factor of 0.85. How much electrical energy do they consume in 1 hour? Power Line Calculation If you want to deliver 1,500 Watts at 100 Volts over transmission lines w/ resistance of 5 Ohms. How much power is lost in the lines? Current Delivered: I P/V 15 Amps Loss IV (on line) I2 R 15*15 * 5 1,125 Watts! If you deliver 1,500 Watts at 10,000 Volts over the same transmission lines. How much power is lost? Current Delivered: I P/V .15 Amps Loss IV (on line) I 2R 0.125 Watts Lower, but not zero!!! Cost to you Utility companies charge a surcharge for industrial customers with large power factors (e.g. large AC loads). Customers can correct power factor with capacitors. Assumed power factor for residential > 0.95. Warning!!!! About to talk about “Quality Factor”, Q Just to confuse you….we’re also going to be talking about the charge on a capacitor, Q We’ll go through the math quickly…. Hang in there. We’ll show what it means conceptually and do an example problem in the end. Electricity & Magnetism Lecture 21, Slide 18 Recall Damped Harmonic Motion Q QMax e t cos( ' t ) Damping factor R 2L Natural oscillation frequency 1 LC Damped oscillation frequency '2 o2 2 Unit 19, Slide 19 What does Q mean algebraically…. Energy Charge2 Energy Lost (e t 2 ) e Define Quality Factor I Q I Q 2 rms 2 rms t /( L / R ) Q o L R o 1 LC 2 L I rms L( f o 2 ) o 2 I R rms R (Maximum energy Stored) = 2 (Energy Lost per Cycle) Unit 19, Slide 20 Second way to look at Q I max Vgen R (X L XC ) 2 2 Vgen 1 R ( x 1) 1 Q 2 x 2 2 2 How fast you fall away from current at resonance x o How far you are from resonance Bigger Q, fall off faster Unit 19, Slide 21 Q=0.5 Q=1.0 Imax/(e/R) Imax/(e/R) What does Q mean graphically….. x=/o Q=5.0 Imax/(e/R) Imax/(e/R) x=/o x=/o Q=20.0 x=/o Useful approximation from Q Often used approximation for Q>2 o Q FWHM “Full Width at Half Maximum” Q=5.0 Example 21.5 (FWHM) An electronic filter is made up of an inductor, L=0.5H, a capacitor, C=2.0uF and resistor, R=20W. It has an input signal with Vmax = 0.1V. 1) What is the resonant frequency for this filter? 2) What is the average output power at this frequency? 3) What is the quality factor Q for this filter? 4) Use this Q to estimate FWHM. 5) What is the average power output at a frequency of o + FWHM/2? Electricity & Magnetism Lecture 21, Slide 24 Transformers Primary (P) DVP DIP DBP DFS DIS DVS DBS DFP Secondary (S) Difficult to calculate step by step Transformers FS FP loop loop eP NP eS NS NS eS eP NP Note by energy PS conservation PP I S NP IP NS Example 21.6 (Coil in your car) In the old days, the high voltage needed to fire the spark plugs in your car was created by “the coil”. On a typical coil, there were 200 turns the primary side and 400,000 turns on the secondary side. If the car’s alternator provided 12 volts to the coil, what was the voltage provided to the spark plugs? Uniy 21, Slide 27