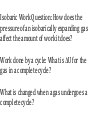Download AP Ch.18 - mrmacphysics

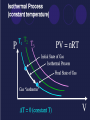
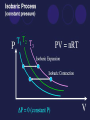
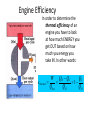
Chapter 18
The Laws of Thermodynamics
Thermodynamics
The study of heat and
its transformation into
mechanical work.
18-1 The Zeroth Law of Thermodynamics
We have already discussed
the zeroth law, and include it
here for completeness:
If object A is in thermal
equilibrium with object C, and
object B is separately in
thermal equilibrium with
object C, then objects A and B
will be in thermal equilibrium
if they are placed in thermal
contact.
Work done by a gas - Suppose you had a piston
filled with a specific amount of gas. As you add
heat, the temperature rises and thus the volume of
the gas expands. The gas then applies a force on the
piston wall pushing it a specific displacement. Thus
it can be said that a gas can do WORK.
Work done BY gas
Work done ON gas
Sample Problem: An engine cylinder compresses a
volume of gas by 0.04 m3. How much work is done
by the cylinder if it exerts a constant pressure of 7.5
x 105 Pa?
Sample problem: Calculate the work done by a gas
that expands from 0.020 m3 to 0.80 m3 at constant
atmospheric pressure. How much work is done by
the environment when the gas expands this much?
Work is the AREA of a P vs. V graph
W   PV
V    Work is done BY the gas
V    Work is done ON the gas
Wby  negative
The “negative” sign in the equation for
WORK is often misunderstood. Since
work done BY a gas has a positive
volume change we must understand
that the gas itself is USING UP ENERGY
or in other words, it is losing energy,
thus the negative sign.
Won  positive
When work is done ON a gas the change in volume is negative. This cancels out the negative
sign in the equation. This makes sense as some EXTERNAL agent is ADDING energy to the gas.
The “negative” sign in the equation for WORK
is often misunderstood. Since work done BY
a gas has a positive volume change we must
understand that the gas itself is USING UP
ENERGY or in other words, it is losing energy,
thus the negative sign.
When work is done ON a gas the change in
volume is negative. This cancels out the
negative sign in the equation. This makes
sense as some EXTERNAL agent is ADDING
energy to the gas.
Example
Sketch a PV diagram and find the
work done by the gas during
the following stages.
(a) A gas is expanded from a
volume of 1.0 L to 3.0 L at a
constant pressure of 3.0 atm.
WBY  PV  3x105 (0.003  0.001)  600 J
(b) The gas is then cooled at a
constant volume until the
pressure falls to 2.0 atm
W  PV  0
since V  0
Example continued
a)
The gas is then compressed
at a constant pressure of 2.0
atm from a volume of 3.0 L
to 1.0 L.
WON   PV  2 x105 (.001  .003)  -400 J
b)
The gas is then heated until
its pressure increases from
2.0 atm to 3.0 atm at a
constant volume.
W  PV  0
since V  0
Example continued
What is the NET
WORK?
600 J + -400 J = 200 J
Rule of thumb: If the system
rotates CW, the NET work is
positive.
If the system rotates CCW, the
NET work is negative.
NET work is
the area inside
the shape.
Sketch a PV diagram and find the work
done by the gas during the following
stages.
(a) A gas is expanded from a volume of 1.0 L to 3.0 L at a
constant pressure of 3.0 atm.
(b) The gas is then cooled at a constant volume until the
pressure falls to 2.0 atm.
(c) What is the net work?
• Rule of thumb: If the
system rotates CW, the NET
work is positive.
• If the system rotates CCW,
the NET work is negative.
Sample problem: Consider the cycle ABCDA, where
State A: 200 kPa, 1.0 m3 State B: 200 kPa, 1.5 m3
State C: 100 kPa, 1.5 m3 State D: 100 kPa, 1.0 m3
•Sketch the cycle.
• B) Graphically estimate the work done by the gas in
one cycle.
• C) Is the work from ABC (more, less, or the
same) as the work from ADC.
• Work is path dependent.
Work done by a cycle
Internal Energy (U)
All of the energy inside a system is called
INTERNAL ENERGY, U.
When you add HEAT(Q), you are adding energy
and the internal energy INCREASES.
Both are measured in joules. But when you add
heat, there is usually an increase in
temperature associated with the change.
The First Law of Thermodynamics
The first law of thermodynamics is a statement of the
conservation of energy.
If a system’s volume is constant, and heat is added, its
internal energy increases.
The First Law of Thermodynamics
If a system does work on the external world,
and no heat is added, its internal energy
decreases.
First Law of Thermodynamics
“The internal energy of a system tend to increase when
HEAT is added and work is done ON the system.”
Suggests a CHANGE or subtraction
U  Q  W  U  QAdd  Won
or U  QAdd  Wby
You are really adding a negative here!
The bottom line is that if you ADD heat then transfer work TO the gas, the
internal energy must obviously go up as you have MORE than what you
started with.
The First Law of Thermodynamics
Combining these gives the first law of thermodynamics. The change in a
system’s internal energy is related to the heat Q and the work W as
follows:
It is vital to keep track of the signs of Q and W.
U = Q + W
U: change in internal energy of system(J)
Q: heat added to the system (J). This heat
exchange is driven by temperature
difference.
W: work done on the system (J). Work will
be related to the change in the system’s
volume.
This law is sometimes paraphrased as “you
can’t win”.
Sample Problem: When 5000 J of heat is added to an
engine, the engine does 1250 J of work. What is the
change in the internal energy of engine?
Sample Problem: A system absorbs 200 J of energy
from the environment and does 100 J of work on
the environment. What is its change in internal
energy?
Sample Problem: How much work does the
environment do on a system if its internal energy
changes from 40,000 J to 45,000 J without the
addition of heat?
• The thermodynamic state of a gas is
defined by pressure, volume, and
temperature.
• A gas process describes how gas gets
from one state to another state.
• Processes depend on the behavior of the
boundary and the environment more
than they depend on the behavior of the
gas.
Isothermal Processes
This is an idealized reversible process. The gas is compressed;
the temperature is constant, so heat leaves the gas. As the
gas expands, it draws heat from the reservoir, returning the
gas and the reservoir to their initial states. The piston is
assumed frictionless.
To keep the temperature
constant both the pressure
and volume change to
compensate. (Volume goes
up, pressure goes down)
“BOYLES’ LAW”
Isobaric Process
Heat is added to the gas which increases the
Internal Energy (U) Work is done by the gas as
it changes in volume.
The path of an isobaric process is a horizontal
line called an isobar.
∆U = Q - W can be used since the WORK is
POSITIVE in this case
Isovolumetric or Isometric Process
Thermodynamic Processes - Adiabatic
ADIABATIC- (GREEKadiabatos"impassable")
In other words, NO HEAT
can leave or enter the
system.
An adiabatic process is one in which no heat flows
into or out of the system. The adiabatic P-V curve is
similar to the isothermal one, but is steeper. One way
to ensure that a process is adiabatic is to insulate the
system.
18-3 Thermal Processes
Another way to ensure that a process is
effectively adiabatic is to have the
volume change occur very quickly. In this
case, heat has no time to flow in or out
of the system.
Isobaric Work Question: How does the
pressure of an isobarically expanding gas
affect the amount of work it does?
Work done by a cycle: What is U for the
gas in a complete cycle?
What is changed when a gas undergoes a
complete cycle?
18-3 Thermal Processes
Here is a summary of the different types of thermal processes:
In Summary
Second Law of Thermodynamics
•
No process is possible whose sole result is the
complete conversion of heat from a hot
reservoir into mechanical work. (Kelvin-Planck
statement.)
“
• No process is possible whose sole result is the
transfer of heat from a cooler to a hotter
body. (Clausius statement.)
The bottom line:
1) Heat always flows from a hot body to a cold body
2) Nothing is 100% efficient
Heat engines can convert
heat into useful work.
• According to the 2nd Law of Thermodynamics. Heat
engines always produce some waste heat.
• Efficiency can be used to tell how much heat is
needed to produce a given amount of work.
• NOTE: A heat engine is not something that
produces heat. A heat engine transfers heat from
hot to cold, and does mechanical work in the
process.
Heat Transfer
Heat Engine
Engines
Heat flows from a HOT
reservoir to a COLD reservoir
QH  W  QC
Woutput  QH  QC
QH = remove from, absorbs = hot
QC= exhausts to, expels = cold
Engine Efficiency
In order to determine the
thermal efficiency of an
engine you have to look
at how much ENERGY you
get OUT based on how
much you energy you
take IN. In other words:
QH  QC
QC
W
ethermal 

 1
Qhot
QH
QH
• In order to reverse heat flow
work must be done.
• Spontaneous flow of heat from a
cold area to a hot area would
constitute a perfect refrigerator,
forbidden by the second law.
Sample Problem: A piston absorbs 3600 J of heat and
dumps 1500 J of heat during a complete cycle. How
much work does it do during the cycle?
What is the efficiency?
Carnot Cycle
Carnot Efficiency
Carnot a believed that there was an absolute
zero of temperature, from which he figured
out that on being cooled to absolute zero,
the fluid would give up all its heat
energy. Therefore, if it falls only half way to
absolute zero from its beginning
temperature, it will give up half its heat, and
an engine taking in heat at T and shedding it
at ½T will be utilizing half the possible heat,
and be 50% efficient. Picture a water wheel
that takes in water at the top of a waterfall,
but lets it out halfway down. So, the
efficiency of an ideal engine operating
between two temperatures will be equal to
the fraction of the temperature drop
towards absolute zero that the heat
undergoes.
Efficiency of a Carnot Cycle
Sample Problem: Calculate the Carnot efficiency of a
heat engine operating between the temperatures of
60 and 1500 oC.
Entropy