* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Current source wikipedia , lookup
Ground (electricity) wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Alternating current wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Voltage optimisation wikipedia , lookup
Electrical substation wikipedia , lookup
Regenerative circuit wikipedia , lookup
Circuit breaker wikipedia , lookup
Rectiverter wikipedia , lookup
Stray voltage wikipedia , lookup
Zobel network wikipedia , lookup
Mains electricity wikipedia , lookup
Electronic engineering wikipedia , lookup
Opto-isolator wikipedia , lookup
Three-phase electric power wikipedia , lookup
Two-port network wikipedia , lookup
MICROSYSTEMS LABORATORY
DEPARTMENT OF ELECTRICAL &
COMPUTER ENGINEERING
A CMOS Voltage Adjustable All-Pass Circuit
Robert W. Newcomb
Talk for SWAN 06
December 8, 2006
(Systems Workshop on Adaptive & Networks)
At the Automation and Robotics Research Institute
The University of Texas at Arlington
2
With Great Thanks to, and Respect for,
Frank Lewis
And especially for taking the initiative to
Organize SWAN 06
3
Main topic of this talk:
The design of a VLSI all-pass CMOS circuit
for variable phase controlled by a voltage .
Possible uses:
An alternate type of phase locked loop
(may have a phase noise advantage)
Phase correction for various purposes.
Outline:
The degree one circuit of Maundy-Aronhime;
Generalization to any degree
Conversion to VLSI transistors; VLSI layout
Spice simulations; MathCad symbolic analysis
At end: Some Microsystems research topics.
4
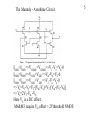
The ideas are based upon the circuit of Maundy & Aronhime.
Their circuit gives
Vout=2*V3-Vin
Using the RC voltage divider V3={(1/sC)/[R+(1/sC)]}Vin
which is
V3={1/[1+sRC]}Vin
gives the degree one all-pass transfer function
Vout/Vin=[1-sRC]/[1+sRC] = T(s)=1/T(-s)
Angle T(jw) = -2*arctan(RCw); |T(jw)|=1
Reference: B. J. Maundy & P. Aronhime, "A Novel First-Order AllPass Filter," International Journal of Electronics, Vol. 89, No. 9,
2002, pp. 739 - 743.
The Maundy - Aronhime Circuit
IDM2=IDM1=>VGSM1=VGSM2=>V3-Vx=Vb-0
IDM4=IDM3=>VGS4=VGS3=>Vin-Vy=Vx-0
IDM6=IDM5=>VGS6=VGS5=>V3-Vo=Vy-0
=> Vo=V3-Vy=V3-[Vin-Vx]=V3-[Vin-(V3-Vb)]
=> Vo=2V3-Vin -Vb
Here Vb is a DC offset;
M4&M3 require Vin offset > 2Vthreshold NMOS
5
Generalization to arbitrary rational all-pass
T(s)
D(-s)
N(s) Vout
T( )
D(s)
V
D(s)
in
with D(s) Hurwitz and monic (1)
set
V
Vout
T( ) * (2( 3 ) 1)
V
V
in
in
(1) into (2)
V
3 ( 1 ) * ( 1 Vout 1) [(D(s) D( s)]/2
V
2
T( ) Vin
D(s)
in
or
V
Ev[D(s)]
z(s)/R
z(s)
3
V
Ev[D(s)] Od[D(s)] 1 z(s)/R R z(s)
in
zs / R Ev[D(s)]/O d[D(s)]
(2)
where z(s) R * Ev[D(s)]/O d[D(s)] is a reactance function and, therefore , z(s) is synthesiza ble as
the driving point impedance of a lossless 1 - port.
6
Transistorization for VLSI and with variable R
7
8
Spice run: Phase in degrees
Spice run: Magnitude in DB
9
Bias conditions for proper operation
Need to account for offsets due to substrates of M2, M4, M6
Not connected to their sources; adds [(-Vbs)^½-^½] to VTO
10
11
Small Signal Analysis
By replacing each transistor by its pi equivalent, and
Numbering x=4, y=5, ground=6, the indefinite Y matrix
is obtained. Deleting the 6th row and column yields the
nodal admittance matrix.
0
s Cg gor
0
s Cg gm6 go5 go6
Y11( s )
gor
s Cgs
Y21( s )
0
0
s Cgs gm4 s Cgd
gor
0
s Cgs
s Cgs gm6 0 s Cgd gm5
Y12( s )
s Cgs
0
s C3 gor
Y22( s ) s Cgs gm2 s ( 2 Cg) gm2 go2 go1
s Cgd
*
0
s
Cgd
gm3
s
(
2
Cg
)
gm4
go4
go3
Form the 2-port Y(s)=Y11-Y12*Z22*Y21 where Z22=Y22^-1
From which: T(s)=-Y(s)[2,1]/Y(s)[2,2]
Display by float 4 to 4 digits and then solve, for the poles and
zeros at different resistor control voltages, Vr.
12
Using MathCad symbolic analysis, by eliminating
Internal nodes (3,4,5) the transfer function is obtained
At Vr=1;
T1( s ) .1000e-1
3
2
4
3
.3408e59 s .4601e71 s .4245e82 s .1936e89 .5113e48 s
2
.3336e47 s .1436e59 s .1552e70 s .4136e80 s .1892e87
280224017903.14247865
110019883211.21689326
T1poles
40207159123.703935431
4575253.5434072945902
At Vr=2;
4
T2( s ) .1000e-1
281533881897.68268219
95130927327.539115326
T1zeros
4560434.1831566032044
310006620783.99776471
3
2
4
3
.3407e59 s .4601e71 s .4245e82 s .2394e88 .5113e48 s
2
4
.3336e47 s .1436e59 s .1552e70 s .4136e80 s .2343e86
83119048162807652755.
31070021145535858293.
Poles
12849299996210576479.
2267389.3405606996897
84495397124519949174.
25577256343187389599.
Zeros
2252388.7205777607871
77665064967802876332.
13
Mathcad plots from symbolic transfer function
0
20
40
60
Phase1( w)
Phase2( w)
80
100
120
140
160
180
200
100
10
1 10
3
1 10
1 10
4
5
1 10
6
1 10
7
w
A1( w)
A2( w)
1
0.1
100
1 10
3
1 10
1 10
4
5
w
1 10
6
1 10
7
VLSI Layout for 1.2U AMI fabrication
Vdd
Vr
14
6 main transistors
10ux10u, cap 38ux32u
Out
In
Vb
Gnd
Other research topics of Microsystems Laboratory:
1. Use of ABR (=Acoustic Brain-Stem Response) for
characterizing hearing loss and creation of hearing aids.
Possible use for control of Parkinsons' disease.
2. Use of Beeler-Reuter heart models for VLSI mimic
of heart electrical control for effect of drugs on
arrythmias.
3. Spice models for flexible transistor circuit design.
4. Spice models of DNA electrical characterization
and use of braid group models of DNA type structures.
5. Use of nano sized Y-junctions for room temperature
nano-computers based upon electron swarms.
6. Neural networks using single electron quantum dots.
7. VLSI realization of Prof. Roa’s neural simulink model
incorporating Ca channels.
8. Wireless data collection for on patient sensors
15