* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Oscilloscope types wikipedia , lookup
Waveguide filter wikipedia , lookup
Instrument amplifier wikipedia , lookup
Operational amplifier wikipedia , lookup
Analog-to-digital converter wikipedia , lookup
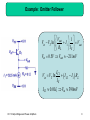
Phase-locked loop wikipedia , lookup
Flexible electronics wikipedia , lookup
Oscilloscope history wikipedia , lookup
Index of electronics articles wikipedia , lookup
Broadcast television systems wikipedia , lookup
Coupon-eligible converter box wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Telecommunication wikipedia , lookup
Audio power wikipedia , lookup
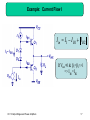
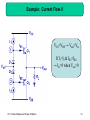
Electronic engineering wikipedia , lookup
Mechanical filter wikipedia , lookup
Digital electronics wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Power electronics wikipedia , lookup
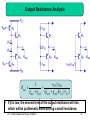
Switched-mode power supply wikipedia , lookup
Audio crossover wikipedia , lookup
Integrated circuit wikipedia , lookup
Transistor–transistor logic wikipedia , lookup
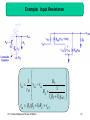
Valve RF amplifier wikipedia , lookup
Rectiverter wikipedia , lookup
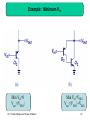
Radio transmitter design wikipedia , lookup
Distributed element filter wikipedia , lookup
Analogue filter wikipedia , lookup
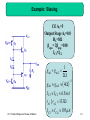
Linear filter wikipedia , lookup
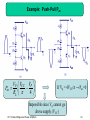
Chapter 13 Output Stages and Power Amplifiers 13.1 13.2 13.3 13.4 13.5 13.6 13.7 13.8 13.9 General Considerations Emitter Follower as Power Amplifier Push-Pull Stage Improved Push-Pull Stage Large-Signal Considerations Short Circuit Protection Heat Dissipation Efficiency Power Amplifier Classes 1 Why Power Amplifiers? Drive a load with high power. Cell phone needs 1W of power at the antenna. Audio system needs tens to hundreds Watts of power. Ordinary Voltage/Current amplifiers are not equipped for such applications CH 13 Output Stages and Power Amplifiers 2 Chapter Outline CH 13 Output Stages and Power Amplifiers 3 Power Amplifier Characteristics Experiences small load resistance. Delivers large current levels. Requires large voltage swings. Draws a large amount of power from supply. Dissipates a large amount of power, therefore gets “hot”. CH 13 Output Stages and Power Amplifiers 4 Power Amplifier Performance Metrics Linearity Power Efficiency Voltage Rating CH 13 Output Stages and Power Amplifiers 5 Emitter Follower Large-Signal Behavior I As Vin increases Vout also follows and Q1 provides more current. CH 13 Output Stages and Power Amplifiers 6 Emitter Follower Large-Signal Behavior II However as Vin decreases, Vout also decreases, shutting off Q1 and resulting in a constant Vout. CH 13 Output Stages and Power Amplifiers 7 Example: Emitter Follower Vout 1 Vin VT ln I1 Vout IS RL Vin 0.5V Vout 211mV I C1 Vin VT ln I C1 I1 RL IS I C1 0.01I1 Vin 390mV CH 13 Output Stages and Power Amplifiers 8 Linearity of an Emitter Follower As Vin decreases the output waveform will be clipped, introducing nonlinearity in I/O characteristics. CH 13 Output Stages and Power Amplifiers 9 Push-Pull Stage As Vin increases, Q1 is on and pushes a current into RL. As Vin decreases, Q2 is on and pulls a current out of RL. CH 13 Output Stages and Power Amplifiers 10 I/O Characteristics for Large Vin Vout=Vin-VBE1 for large +Vin Vout=Vin+|VBE2| for large -Vin For positive Vin, Q1 shifts the output down and for negative Vin, Q2 shifts the output up. CH 13 Output Stages and Power Amplifiers 11 Overall I/O Characteristics of Push-Pull Stage However, for small Vin, there is a dead zone (both Q1 and Q2 are off) in the I/O characteristic, resulting in gross nonlinearity. CH 13 Output Stages and Power Amplifiers 12 Small-Signal Gain of Push-Pull Stage The push-pull stage exhibits a gain that tends to unity when either Q1 or Q2 is on. When Vin is very small, the gain drops to zero. CH 13 Output Stages and Power Amplifiers 13 Sinusoidal Response of Push-Pull Stage For large Vin, the output follows the input with a fixed DC offset, however as Vin becomes small the output drops to zero and causes “Crossover Distortion.” CH 13 Output Stages and Power Amplifiers 14 Improved Push-Pull Stage VB=VBE1+|VBE2| With a battery of VB inserted between the bases of Q1 and Q2, the dead zone is eliminated. CH 13 Output Stages and Power Amplifiers 15 Implementation of VB Since VB=VBE1+|VBE2|, a natural choice would be two diodes in series. I1 in figure (b) is used to bias the diodes and Q1. CH 13 Output Stages and Power Amplifiers 16 Example: Current Flow I I in I1 I B1 I B 2 Iin CH 13 Output Stages and Power Amplifiers If Vout=0 & β1=β2>>1 => IB1=IB2 17 Example: Current Flow II VD1≈VBE → Vout≈Vin If I1=I2 & IB1≈IB2 → Iin=0 when Vout=0 CH 13 Output Stages and Power Amplifiers 18 Addition of CE Stage A CE stage (Q4) is added to provide voltage gain from the input to the bases of Q1 and Q2. CH 13 Output Stages and Power Amplifiers 19 Bias Point Analysis VA=0 Vout=0 IC1=[IS,Q1/IS,D1]×[IC3] For bias point analysis, the circuit can be simplified to the one on the right, which resembles a current mirror. The relationship of IC1 and IQ3 is shown above. CH 13 Output Stages and Power Amplifiers 20 Small-Signal Analysis AV=-gm4(rπ1||r π2)(gm1+gm2)RL Assuming 2rD is small and (gm1+gm2)RL is much greater than 1, the circuit has a voltage gain shown above. CH 13 Output Stages and Power Amplifiers 21 Output Resistance Analysis Rout rO3 || rO 4 1 g m1 g m 2 ( g m1 g m 2 )(r 1 || r 2 ) If β is low, the second term of the output resistance will rise, which will be problematic when driving a small resistance. CH 13 Output Stages and Power Amplifiers 22 Example: Biasing CE AV=5 Output Stage AV=0.8 RL=8Ω βnpn= 2βpnp=100 IC1≈IC2 g m1 g m 2 1 2 g m1 g m 2 4 1 I C1 I C 2 6.5mA r 1 || r 2 133 CH 13 Output Stages and Power Amplifiers I C 3 I C 4 195 A 23 Problem of Base Current 195 µA of base current in Q1 can only support 19.5 mA of collector current, insufficient for high current operation (hundreds of mA). CH 13 Output Stages and Power Amplifiers 24 Modification of the PNP Emitter Follower Rout 1 2 1 g m3 Instead of having a single PNP as the emitter-follower, it is now combined with an NPN (Q2), providing a lower output resistance. CH 13 Output Stages and Power Amplifiers 25 Example: Input Resistance RL 1 iin vin vin 1 r 3 RL 2 1 g m3 rin 3 ( 2 1) RL r 3 CH 13 Output Stages and Power Amplifiers 26 Additional Bias Current I1 is added to the base of Q2 to provide an additional bias current to Q3 so the capacitance at the base of Q2 can be charged/discharged quickly. CH 13 Output Stages and Power Amplifiers 27 Example: Minimum Vin Min Vin≈0 Vout≈|VEB2| CH 13 Output Stages and Power Amplifiers Min Vin≈VBE2 Vout≈|VEB3|+VBE2 28 HiFi Design Using negative feedback, linearity is improved, providing higher fidelity. CH 13 Output Stages and Power Amplifiers 29 Short-Circuit Protection Qs and r are used to “steal” some base current away from Q1 when the output is accidentally shorted to ground, preventing short-circuit damage. CH 13 Output Stages and Power Amplifiers 30 Emitter Follower Power Rating VP Pav I1 VCC 2 Pav ,max T1VCC Maximum power dissipated across Q1 occurs in the absence of a signal. CH 13 Output Stages and Power Amplifiers 31 Example: Power Dissipation Avg Power Dissipated in I1 1 T PI 1 I1 V p sin t VEE dt T 0 PI 1 I1VEE CH 13 Output Stages and Power Amplifiers 32 Push-Pull Stage Power Rating VP VCC VP Pav RL 4 Pav,max 2 VCC 2 RL Maximum power occurs between Vp=0 and 4Vcc/π. CH 13 Output Stages and Power Amplifiers 33 Example: Push-Pull Pav VP VCC VP Pav RL 4 If Vp = 4VCC/π → Pav=0 Impossible since Vp cannot go above supply (VCC) CH 13 Output Stages and Power Amplifiers 34 Heat Sink Heat sink, provides large surface area to dissipate heat from the chip. CH 13 Output Stages and Power Amplifiers 35 Thermal Runaway Mitigation I C1 I C 2 I D1I D 2 I S , D1I S , D 2 I S ,Q1I S ,Q 2 Using diode biasing prevents thermal runaway since the currents in Q1 and Q2 will track those of D1 and D2 as long as theie Is’s track with temperature. CH 13 Output Stages and Power Amplifiers 36 Efficiency Pout Pout Pckt Emitter Follower EF EF VP2 VP2 2 RL 2 RL I1 2VCC VP 2 VP 4VCC I1=VP/RL Push-Pull Stage PP VP2 VP2 2 RL 2 RL 2 I1 VCC / VP 4 PP VPVCC 4 I1=VP/RL Efficiency is defined as the average power delivered to the load divided by the power drawn from the supply CH 13 Output Stages and Power Amplifiers 37 Example: Efficiency Emitter Follower VP=VCC/2 1 15 CH 13 Output Stages and Power Amplifiers Push-Pull I1=(VP/RL)/β VP 1 4 VCC VP 38 Power Amplifier Classes Class A: High linearity, low efficiency Class B: High efficiency, low linearity Class AB: Compromise between Class A and B CH 13 Output Stages and Power Amplifiers 39 Chapter 14 Analog Filters 14.1 14.2 14.3 14.4 14.5 General Considerations First-Order Filters Second-Order Filters Active Filters Approximation of Filter Response 40 Outline of the Chapter CH 14 Analog Filters 41 Why We Need Filters In order to eliminate the unwanted interference that accompanies a signal, a filter is needed. CH 14 Analog Filters 42 Filter Characteristics Ideally, a filter needs to have a flat pass band and a sharp rolloff in its transition band. Realistically, it has a rippling pass/stop band and a transition band. CH 14 Analog Filters 43 Example: Filter I Given: Adjacent channel Interference is 25 dB above the signal Design goal: Signal to Interference ratio of 15 dB Solution: A filter with stop band of 40 dB CH 14 Analog Filters 44 Example: Filter II Given: Adjacent channel Interference is 40 dB above the signal Design goal: Signal to Interference ratio of 20 dB Solution: A filter with stop band of 60 dB at 60 Hz CH 14 Analog Filters 45 Example: Filter III A bandpass filter around 1.5 GHz is needed to reject the adjacent Cellular and PCS signals. CH 14 Analog Filters 46 Classification of Filters I CH 14 Analog Filters 47 Classification of Filters II Continuous-time CH 14 Analog Filters Discrete-time 48 Classification of Filters III Passive CH 14 Analog Filters Active 49 Summary of Filter Classifications CH 14 Analog Filters 50 Filter Transfer Function A B Filter a) has a transfer function with -20dB/dec roll-off Filter b) has a transfer function with -40dB/dec roll-off, better selectivity. CH 14 Analog Filters 51 General Transfer Function s Z1 s Z 2 s Z m H ( s) s P1 s P2 s Pm CH 14 Analog Filters Zm=m’th zero Pn =n’th pole 52 Pole-Zero Diagram CH 14 Analog Filters 53 Position of the Poles Poles on the RHP Unstable (no good) CH 14 Analog Filters Poles on the jω axis Oscillatory (no good) Poles on the LHP Decaying (good) 54 Imaginary Zero Imaginary zero is used to create a null at certain frequency. CH 14 Analog Filters 55 Sensitivity dP P SC P dC C P=Parameter C=Component Sensitivity measures the variation of a filter parameter due to variation of a filter component. CH 14 Analog Filters 56 Example: Sensitivity 0 1 / R1C1 d0 1 dR1 R12C1 d0 dR1 0 R1 S R10 1 CH 14 Analog Filters 57 First-Order Filters s z1 H ( s) s p1 First-order filters are represented by the transfer function shown above. Low/high pass filters can be realized by changing the relative positions of poles and zeros. CH 14 Analog Filters 58 Example: First-Order Filter I R2C 2 < R1C1 CH 14 Analog Filters R2C2 > R1C1 59 Example: First-Order Filter II CH 14 Analog Filters R2C2 < R1C 1 R2C2 > R1C1 60 Second-Order Filters s2 s H ( s) 2 n s s n2 Q p1,2 n 2Q jn 1 1 4Q2 Second-order filters are characterized by the “biquadratic” equation with two complex poles shown above. CH 14 Analog Filters 61 Second-Order Low-Pass Filter H ( j ) 2 2 n2 CH 14 Analog Filters 2 2 n Q 2 α=β=0 62 Example: Second-Order LPF Q3 Q / 1 1/(4Q 2 ) 3 n 1 1/(2Q 2 ) n CH 14 Analog Filters 63 Second-Order High-Pass Filter H ( s) s2 CH 14 Analog Filters s2 n Q s n2 β=γ=0 64 Second-Order Band-Pass Filter H ( s) s 2 CH 14 Analog Filters s n Q 2 s n α=γ=0 65 Example: -3-dB Bandwidth R1L1s Z2 R1L1C1s 2 L1s R1 CH 14 Analog Filters 66 LC Realization of Second-Order Filters L1s Z1 L1C1s 2 1 An LC tank realizes a second-order band-pass filter with two imaginary poles at ±j/(L1C1)1/2 , which implies infinite impedance at ω=1/(L1C1)1/2. CH 14 Analog Filters 67 Example: Tank ω=0, the inductor acts as a short. ω=∞, the capacitor acts as a short. CH 14 Analog Filters 68 RLC Realization of Second-Order Filters R1L1s Z2 R1L1C1s 2 L1s R1 p1,2 L 1 1 j 1 21 2 R1C1 4 R1 C1 L1C1 With a resistor, the poles are no longer pure imaginary which implies there will be no infinite impedance at any ω. CH 14 Analog Filters 69 Voltage Divider Using General Impedances Vout ZP ( s) Vin ZS ZP Low-pass CH 14 Analog Filters High-pass Band-pass 70 Low-pass Filter Implementation with Voltage Divider Vout R1 s 2 Vin R1C1L1s L1s R1 CH 14 Analog Filters 71 Example: Frequency Peaking Vout R1 s Vin R1C1L1s 2 L1s R1 1 Q 2 CH 14 Analog Filters Peaking exists Voltage gain larger than unity 72 Low Pass Circuit Comparison Good Bad The circuit on the left has a sharper roll-off at high frequency than the circuit on the right. CH 14 Analog Filters 73 High-pass Filter Implementation with Voltage Divider Vout L1C1R1s 2 s 2 Vin R1C1L1s L1s R1 CH 14 Analog Filters 74 Band-pass Filter Implementation with Voltage Divider 2 Vout L1s s 2 Vin R1C1L1s L1s R1 CH 14 Analog Filters 75 Sallen and Key (SK) Filter: Low-Pass Vout 1 s Vin R1R2C1C2 s 2 R1 R2 C2 s 1 1 Q R1 R2 C R1R2 1 C2 n 1 R1R2C1C2 Sallen and Key filters are examples of active filters. This particular filter implements a low-pass, second-order transfer function. CH 14 Analog Filters 76 Sallen and Key (SK) Filter: Band-pass Vout s Vin CH 14 Analog Filters R3 1 R4 R3 R1R2C1C2 s R1C2 R2C2 R1 C1 s 1 R4 2 77 Example: SK Filter Poles C1=C2 R1=R2 CH 14 Analog Filters 78 Sensitivity in Band-Pass SK Filter n n n n S R S R SC SC 1 S RQ 1 2 S RQ 2 1 2 1 2 R2C2 1 Q 2 R1C1 CH 14 Analog Filters SCQ 1 SCQ 2 R2C2 R1C2 1 Q 2 R2C1 R1C1 S KQ QK R1C1 R2C2 K=1+R3/R4 79 Example: SK Filter Sensitivity I R1 R2 R C1 C2 C S RQ 1 S RQ 2 SCQ SCQ 1 S KQ CH 14 Analog Filters 2 1 1 2 3 K 1 2 2 3 K K 3 K 80 Example: SK Filter Sensitivity II Q2 K 2 R2C2 3 S RQ 1 1 R1C1 4 R1C1 1 5 Q SC 1 R2C2 8 4 S KQ CH 14 Analog Filters 8 1.5 81 Integrator-Based Biquads Vout s2 s Vin 2 n s s n2 Q Vout s Vin s n 1 n2 . Vout s 2 Vout s Q s s It is possible to use integrators to implement biquadratic transfer functions. The block-diagram above illustrates how. CH 14 Analog Filters 82 KHN Biquads Vout s Vin s R5 R6 1 R4 R5 R3 CH 14 Analog Filters n n 1 n2 . Vout s 2 Vout s Q s s R4 1 . Q R4 R5 R1C1 n2 R6 1 . R3 R1R2C1C2 83 Versatility of KHN Biquads High-Pass Vout s2 s Vin s 2 n s n2 Q Band-Pass VX s2 1 . s Vin s 2 n s n2 R1C1s Q CH 14 Analog Filters Low-Pass VY s2 1 . s 2 Vin 2 n 2 R1R2C1C2 s s s n Q 84 Sensitivity in KHN Biquads SRn,R ,C ,C ,R ,R ,R ,R 0.5 1 2 1 2 4 5 3 6 SRQ ,R ,C ,C 0.5 1 S RQ , R 3 6 Q R3 R6 2 1 R5 R4 CH 14 Analog Filters R2C2 R 3 R6 R1C1 S RQ , R 4 5 2 1 2 R5 1 R4 R5 85 Tow-Thomas Biquad Vout RRR C2 s 2 3 4. Vin R1 R2 R3 R4C1C2 s 2 R2 R4C2 s R3 Band-Pass CH 14 Analog Filters VY R3 R4 1 . Vin R1 R2 R3 R4C1C2 s 2 R2 R4C2 s R3 Low-Pass 86 Example: Tow-Thomas Biquad n 1 R2 R4C1C2 Adjusted by R2 or R4 CH 14 Analog Filters 1 Q R3 R2 R4C2 C1 Adjusted by R3 87 Differential Tow-Thomas Biquads By using differential integrators, the inverting stage is eliminated. CH 14 Analog Filters 88 Simulated Inductor (SI) Z1Z3 Zin Z5 Z2 Z4 It is possible to simulate the behavior of an inductor by using active circuits in feedback with properly chosen passive elements. CH 14 Analog Filters 89 Example: Simulated Inductor I Zin 2 RX RY Cs By proper choices of Z1-Z4, Zin has become an impedance that increases with frequency, simulating inductive effect. CH 14 Analog Filters 90 Example: Simulated Inductor II Z1 Z 2 Z3 RY CH 14 Analog Filters 1 Z4 Cs Zin RX RY2Cs 91 High-Pass Filter with SI Vout L1s 2 s Vin R1C1L1s 2 L1s R1 With the inductor simulated at the output, the transfer function resembles a second-order high-pass filter. CH 14 Analog Filters 92 Example: High-Pass Filter with SI Node 4 is also an output node CH 14 Analog Filters RY V4 Vout 1 RX 93 Low-Pass Filter with Super Capacitor 1 Zin Cs RX Cs 1 Vout Zin 1 Vin Zin R1 R1RX C 2 s 2 R1Cs 1 Low-Pass CH 14 Analog Filters 94 Example: Poor Low Pass Filter V4 Vout 2 RX Cs Node 4 is no longer a scaled version of the Vout. Therefore the output can only be sensed at node 1, suffering from a high impedance. CH 14 Analog Filters 95 Frequency Response Template With all the specifications on pass/stop band ripples and transition band slope, one can create a filter template that will lend itself to transfer function approximation. CH 14 Analog Filters 96 Butterworth Response H ( j ) 1 1 0 2n ω-3dB=ω0, for all n The Butterworth response completely avoids ripples in the pass/stop bands at the expense of the transition band slope. CH 14 Analog Filters 97 Poles of the Butterworth Response j 2k 1 pk 0 exp exp j , k 1, 2, 2 2n CH 14 Analog Filters 2nd-Order ,n nth-Order 98 Example: Butterworth Order f2 f1 2n 64.2 f 2 2 f1 n=3 The Butterworth order of three is needed to satisfy the filter response on the left. CH 14 Analog Filters 99 Example: Butterworth Response 2 2 p1 2 *(1.45MHz ) * cos j sin 3 3 2 2 p3 2 *(1.45MHz ) * cos j sin 3 3 CH 14 Analog Filters RC section 2nd-Order SK p2 2 *(1.45MHz ) 100 Chebyshev Response 1 H j 1 2 2 Cn 0 Chebyshev Polynomial The Chebyshev response provides an “equiripple” pass/stop band response. CH 14 Analog Filters 101 Chebyshev Polynomial Chebyshev Polynomial for n=1,2,3 Resulting Transfer function for n=2,3 1 Cn cos n cos , 0 0 0 CH 14 Analog Filters 1 cosh n cosh , 0 0 102 Example: Chebyshev Attenuation H j 1 3 2 1 0.329 4 3 0 0 ω0=2π X (2MHz) A third-order Chebyshev response provides an attenuation of 18.7 dB a 2MHz. CH 14 Analog Filters 103 2 Example: Chebyshev Order Passband Ripple: 1 dB Bandwidth: 5 MHz Attenuation at 10 MHz: 30 dB What’s the order? 1 1 0.509 cosh 2 CH 14 Analog Filters 2 n cosh 2 1 0.0316 n>3.66 104 Example: Chebyshev Response pk 0 sin 2k 1 sinh 1 sinh 1 1 j 2n n 0 cos 2k 1 cosh 1 sinh 1 1 2n n K=1,2,3,4 p1,4 0.1400 0.983 j0 SK1 CH 14 Analog Filters p2,3 0.3370 0.407 j0 SK2 105 Chapter 15 Digital CMOS Circuits 15.1 General Considerations 15.2 CMOS Inverter 15.3 CMOS NOR and NAND Gates 106 Chapter Outline CH 15 Digital CMOS Circuits 107 Inverter Characteristic _ XA An inverter outputs a logical “1” when the input is a logical “0” and vice versa. CH 15 Digital CMOS Circuits 108 NMOS Inverter Ron1 1 nCox W (VDD VTH ) L The CS stage resembles a voltage divider between RD and Ron1 when M1 is in deep triode region. It produces VDD when M1 is off. CH 15 Digital CMOS Circuits 109 Transition Region Gain Infinite Transition Region Gain Finite Transition Region Gain Ideally, the VTC of an inverter has infinite transition region gain. However, practically the gain is finite. CH 15 Digital CMOS Circuits 110 Example: Transition Gain Transition Region: 50 mV Supply voltage: 1.8V V0 – V2: Transition Region CH 15 Digital CMOS Circuits Av 1.8 36 0.05 111 Logical Level Degradation Since real power buses have losses, the power supply levels at two different locations will be different. This will result in logical level degradation. CH 15 Digital CMOS Circuits 112 Example: Logic Level Degradation Supply B=1.675V Supply A=1.8V V 5 A 25m 125mV CH 15 Digital CMOS Circuits 113 The Effects of Level Degradation and Finite Gain In conjunction with finite transition gain, logical level degradation in succeeding gates will reduce the output swings of gates. CH 15 Digital CMOS Circuits 114 Small-Signal Gain Variation of NMOS Inverter As it can be seen, the small-signal gain is the largest in the transition region. CH 15 Digital CMOS Circuits 115 Above Unity Small-Signal Gain The magnitude of the small-signal gain in the transition region can be above 1. CH 15 Digital CMOS Circuits 116 Noise Margin Noise margin is the amount of input logic level degradation that a gate can handle before the small-signal gain becomes -1. CH 15 Digital CMOS Circuits 117 Example: NMOS Inverter Noise Margin 1: NM L VIL 1 VTH W nCox RD L 1 W 2 Vout VDD nCox RD 2 Vin VTH Vout Vout 2 L Vout V V in TH W 2 2 nCox RD L CH 15 Digital CMOS Circuits 1 Vin=VIH 2: NM H VDD VIH 118 Example: Minimum Vout RD 19 nCox W VDD VTH L To guarantee an output low level that is below 0.05VDD, RD is chosen above. CH 15 Digital CMOS Circuits 119 Dynamic Behavior of NMOS Inverter Gates Since digital circuits operate with large signals and experience nonlinearity, the concept of transfer function is no longer meaningful. Therefore, we must resort to time-domain analysis to evaluate the speed of a gate. It usually takes 3 time constants for the output to transition. CH 15 Digital CMOS Circuits 120 Rise/Fall Time and Delay CH 15 Digital CMOS Circuits 121 Example: Time Constant 19 L2 RDC X n VDD VTH Assuming a 5% degradation in output low level, the time constant at node X is shown above. CH 15 Digital CMOS Circuits 122 Example: Interconnect Capacitance Wire Capacitance per Mircon: 50x10-18 F/µm Total Interconnect Capacitance: 15000X50x10-18 =750 fF Equivalent to 640 MOS FETs with W=0.5µm, L=0.18µm, Cox =13.5fF/µm2 CH 15 Digital CMOS Circuits 123 Power-Delay Product 2 PDP VDD CX The power delay product of an NMOS Inverter can be loosely thought of as the amount of energy the gate uses in each switching event. CH 15 Digital CMOS Circuits 124 Example: Power-Delay Product TPLH 3RDC X PDP I DDVDD 3RDC X 2 PDP 3VDD WLCox CH 15 Digital CMOS Circuits 125 Drawbacks of the NMOS Inverter Because of constant RD, NMOS inverter consumes static power even when there is no switching. RD presents a tradeoff between speed and power dissipation. CH 15 Digital CMOS Circuits 126 Improved Inverter Topology A better alternative would probably have been an “intelligent” pullup device that turns on when M1 is off and vice versa. CH 15 Digital CMOS Circuits 127 Improved Falltime This improved inverter topology decreases falltime since all of the current from M1 is available to discharge the capacitor. CH 15 Digital CMOS Circuits 128 CMOS Inverter A circuit realization of this improved inverter topology is the CMOS inverter shown above. The NMOS/PMOS pair complement each other to produce the desired effects. CH 15 Digital CMOS Circuits 129 CMOS Inverter Small-Signal Model vout g m1 g m 2 rO1 || rO 2 vin When both M1 and M2 are in saturation, the small-signal gain is shown above. CH 15 Digital CMOS Circuits 130 Switching Threshold The switching threshold (VinT) or the “trip point” of the inverter is when Vout equals Vin. If VinT =Vdd/2, then W2/W1=µn/µp CH 15 Digital CMOS Circuits 131 CMOS Inverter VTC CH 15 Digital CMOS Circuits 132 Example: VTC W2 As the PMOS device is made stronger, the VTC is shifted to the right. CH 15 Digital CMOS Circuits 133 Noise Margins VIL NML =VIL NMH =Vdd-VIH 2 a Vdd VTH 1 VTH 2 a 1 a3 Vdd aVTH1 VTH 2 a 1 VIL is the low-level input voltage at which (δVout/ δVin)=-1 VIH 2a Vdd VTH 1 VTH 2 a 1 1 3a Vdd aVTH 1 VTH 2 a 1 VIH is the high-level input voltage at which (δVout/ δVin)=-1 W L 1 a W p L 2 n CH 15 Digital CMOS Circuits 134 VIL of a Symmetric VTC VIL 2 a VDD 2VTH 1 a 3 VDD a 1VTH 1 a 1 a3 Symmetric VTC: a=1 3 1 VIL VDD VTH 1 8 4 CH 15 Digital CMOS Circuits 135 Noise Margins of an Ideal Symmetric VTC NM H ,ideal NM L,ideal CH 15 Digital CMOS Circuits VDD 2 136 Floating Output VTH 1 VDD / 2 VTH 2 VDD / 2 When Vin=VDD/2, M2 and M1 will both be off and the output floats. CH 15 Digital CMOS Circuits 137 Charging Dynamics of CMOS Inverter As Vout is initially charged high, the charging is linear since M2 is in saturation. However, as M2 enters triode region the charge rate becomes sublinear. CH 15 Digital CMOS Circuits 138 Charging Current Variation with Time The current of M2 is initially constant as M2 is in saturation. However as M2 enters triode, its current decreases. CH 15 Digital CMOS Circuits 139 Size Variation Effect to Output Transition As the PMOS size is increased, the output exhibits a faster transition. CH 15 Digital CMOS Circuits 140 Discharging Dynamics of CMOS Inverter Similar to the charging dynamics, the discharge is linear when M1 is in saturation and becomes sublinear as M1 enters triode region. CH 15 Digital CMOS Circuits 141 Rise/Fall Time Delay Rise Time Delay TPLH 2 VTH 2 V ln 3 4 TH 2 V V VDD W pCox VDD VTH 2 DD TH 2 L 2 CL Fall Time Delay TPHL CH 15 Digital CMOS Circuits 2 VTH 1 V ln 3 4 TH 1 V V VDD W nCox VDD VTH 1 DD TH 1 L 1 CL 142 Example: Averaged Rise Time Delay I AVG TPLH 2 1 W pCox VDD VTH 2 4 L 2 CL W VDD VTH 2 L 2 pCox TPLH 2 CH 15 Digital CMOS Circuits . 2 VDD / 2 VDD VTH 2 VDD VTH 2 4 Ron 2CL 3 143 Low Threshold Improves Speed 1st Term TPLH / HL 2 VTH 2 /1 V ln 3 4 TH 2 /1 V V VDD VDD VTH 2 /1 DD TH 2 /1 CL W L 2 /1 p / nCox 2nd Term The sum of the 1st and 2nd terms of the bracket is the smallest when VTH is the smallest, hence low VTH improves speed. CH 15 Digital CMOS Circuits 144 Example: Increased Fall Time Due to Manufacturing Error ' Ron1 || Ron 1 1 W W ' nCox VDD VTH 1 L 1 L 1 2 RON1 Since pull-down resistance is doubled, the fall time is also doubled. CH 15 Digital CMOS Circuits 145 Power Dissipation of the CMOS Inverter 1 2 PDissipation _ PMOS CLVDD fin 2 2 Psupply CLVDD fin 1 2 PDissipation _ NMOS CLVDD fin 2 CH 15 Digital CMOS Circuits 146 Example: Energy Calculation 1 2 Estored CLVDD 2 1 2 Edissipated CLVDD 2 2 Edrawn CLVDD CH 15 Digital CMOS Circuits 147 Power Delay Product 2 2 VTH 1 finCL2VDD VTH 1 PDP ln 3 4 W V V V DD nCox VDD VTH 1 DD TH 1 L 1 Ron1=Ron2 CH 15 Digital CMOS Circuits 148 Example: PDP 4 Ron 3 PDP CH 15 Digital CMOS Circuits 1 W nCox L VDD 2 7.25WL2Cox finVDD n 149 Crowbar Current When Vin is between VTH1 and VDD-|VTH2|, both M1 and M2 are on and there will be a current flowing from supply to ground. CH 15 Digital CMOS Circuits 150 NMOS Section of NOR When either A or B is high or if both A and B are high, the output will be low. Transistors operate as pull-down devices. CH 15 Digital CMOS Circuits 151 Example: Poor NOR The above circuit fails to act as a NOR because when A is high and B is low, both M4 and M1 are on and produces an ill-defined low. CH 15 Digital CMOS Circuits 152 PMOS Section of NOR When both A and B are low, the output is high. Transistors operate as pull-up devices. CH 15 Digital CMOS Circuits 153 CMOS NOR Combing the NMOS and PMOS NOR sections, we have the CMOS NOR. CH 15 Digital CMOS Circuits 154 Example: Three-Input NOR Vout A B C ' Equal Rise & Fall (µn≈2µp) W1=W2=W3=W W4=W5=W6=6W CH 15 Digital CMOS Circuits 155 Drawback of CMOS NOR Due to low PMOS mobility, series combination of M3 and M4 suffers from a high resistance, producing a long delay. The widths of the PMOS transistors can be increased to counter the high resistance, however this would load the preceding stage and the overall delay of the system may not improve. CH 15 Digital CMOS Circuits 156 NMOS NAND Section When both A and B are high, the output is low. CH 15 Digital CMOS Circuits 157 PMOS NOR Section When either A or B is low or if both A and B are low, the output is high. CH 15 Digital CMOS Circuits 158 CMOS NAND Just like the CMOS NOR, the CMOS NAND can be implemented by combining its respective NMOS and PMOS sections, however it has better performance because its PMOS transistors are not in series. CH 15 Digital CMOS Circuits 159 Example: Three-Input NAND Vout ABC ' Equal Rise & Fall (µn≈2µp) W1=W2=W3=3W W4=W5=W6=2W CH 15 Digital CMOS Circuits 160 NMOS and PMOS Duality C is in “series” with the “parallel” combination of A and B C is in “parallel” with the “series” combination of A and B In the CMOS philosophy, the PMOS section can be obtained from the NMOS section by converting series combinations to the parallel combinations and vice versa. CH 15 Digital CMOS Circuits 161