Download 4.5 Transversals and Angles

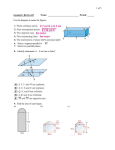
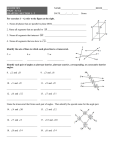
Bellwork

If M(-4, 7) is the midpoint of AB and A is
(-2, 5), find the sum of x and y if the
coordinates of B are (x, y)?

Quarter I Remediation: Given that two
sides of a triangle are 10 and 15, which of
the following could be the length of the
third side?
a. 5
b. 4
c. 25
d. 26
e. 7
4.5 Intro to Parallel Lines
Goal: Students will be able to
identify the special angle
relationships formed by two
lines and a transversal.
Parallel lines (Defn)

Two lines which do not intersect.
Transversal (Defn)

A line that intersects 2 or more lines at
different points.
Pairs of Angles Toolbox!
Interior
Alternate
Same Side
 Exterior
Alternate
Same Side
 Corresponding Angles

Example 1
Determine each pair of angles as alternate interior,
alternate exterior, corresponding, consecutive (same
side) interior or consecutive (same side) exterior.
<1
 <4
 <2
 <3
 <3
 <1

and
and
and
and
and
and
<7
<5
<6
<5
<6
<8
Example 2
Name a pair of angles which are…
 Alternate interior
 Corresponding
 Same side exterior
 Vertical
 Linear Pair
 Alternating exterior
 Same side interior

Example 3
For which pair of lines are
alternate interior angles?
transversal.
 For which pair of lines are
alternate interior angles?
transversal.

<TSV and <SVR
Name the
<TVS and <VSR
Name the
Ticket to Leave

Describe the relationship between
<2 & <12
<3 & <7
<4 & <9
<15 & <6
Homework

Pg. 196 #1-5 all
Notes

Mention Z for Alt Int Angles.
Bellwork:

Do this bellwork on a ½ sheet of paper
and turn in. This is a 5 step proof.
A
Given : E , ABD is isosceles
Pr ove : AC  bis BD
E
B
C
D