Download Document

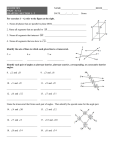
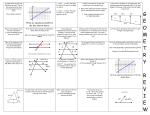
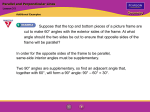
Chapter 3.1
Parallel Lines and Transversals
Relationships Between
Lines and Planes
Parallel Lines – The old definition was
“lines that didn’t intersect”
This definition is now not good enough.
l
Are lines l and
m parallel?
What more
do we need
m in the def?
Parallel Lines
Parallel Lines are coplanar lines that do
not intersect.
The symbol of parallel is this….||.
On diagrams we can use something like
this to indicate that the lines are parallel.
Parallel Planes
Planes can be parallel.
Planes don’t have to be coplanar to be
parallel. As a matter of fact, if planes are
coplanar then they are the same plane.
Example of parallel planes.
Plane AEHD is
parallel to Plane
BFGC.
C
B
D
A
G
F
Any others?
E
H
Skew Lines
Skew lines are lines that are not coplanar.
These lines can never be parallel.
Because they have to be coplanar to be parallel.
They can never intersect.
Because they have to be coplanar to intersect too.
To find Skew lines you need to find noncoplanar
lines.
To do this you could eliminate all…
Parallel Lines
Coplanar Lines
Skew Lines
B
C
D
A
G
F
E
H
Find all lines skew to line AE.
1) Find all lines parallel to line AE. BF DH
2) Eliminate all coplanar lines to line AE.
All remaining lines are Skew to line AE.
CG
Another Example
B
C
D
A
G
F
E
H
Find all lines skew to line BC.
1) Find lines parallel to line BC
2) Find lines coplanar to line BC
AD EH FG
CG BF AB CD
All remaining lines are skew to line BC!
Lines DH, AE, EF and GH are skew to line BC!
Transversals
Transversal – A transversal is line that
intersects two or more coplanar lines in
different places.
Notice the word parallel is not in the
definition.
When a transversal intersects two
coplanar lines in two different places it
creates EIGHT different angles.
Transversals (Con’t)
Two coplanar lines.
A transversal.
Eight angles.
1 2
3 4
5 6
7 8
l
m
n
Think of lines l and m as the rails of a railroad track and
line n as the railroad tie.
If you do, then you will see that the “choo-choo train will
travel right or left on the rails.
Transversals (Con’t)
Thinking of the choo-choo train,
which angles are interior of the
“rails”?
<3, <4, <5 & <6
Which angles are exterior of the
“rails”?
1 2
3 4
5 6
7 8
l
m
n
<1, <2, <7 & <8
Important angle pairs of angles made by a transversal
intersecting a pair of lines.
They are Alternate Interior, Alternate Exterior, Consecutive
Interior, Consecutive Exterior and Corresponding.
Transversal and Angle Pairs
Alternate Interior Angle Pairs –
A pair of interior angles, one per vertex, that
are on alternate sides of the transversal.
Alternate Exterior Angle Pairs –
A pair of exterior angles, one per vertex, that
are on alternate sides of the transversal.
Consecutive Interior Angle Pairs –
A pair of interior angles, one per vertex, that
are on the same side of the transversal.
Consecutive Exterior Angle Pairs –
A pair of exterior angles, one per vertex, that
are on the same side of the transversal.
Transversal and Angle Pairs
Corresponding Angle Pairs –
A pair of angles that “sit on top of each other”
when one vertex is put on top of the other.
Keys to this:
Do you see the word parallel in any of the
definitions?
The angle pairs are one per vertex –
meaning they are not adjacent, nor linear pair.
Transversals and Angle Pairs
Alternate Interior
<3 & <6
<4 & <5
Alternate Exterior
<1 & <8
<2 & <7
Consecutive Exterior
<1 & <7
<2 & <8
1 2
3 4
5 6
7 8
n
Consecutive Interior
<3 & <5
<4 & <6
l
m
Transversals and Angle Pairs
Corresponding Angles
<1 & <5
<2 & <6
<3 & <7
<4 & <8
1 2
3 4
l
5 6
7 8
n
All the angle pairs have been
made by the transversal, line
n, intersecting two lines, l and
m in two different places.
m
Chapter 3.2
Angles and Parallel Lines
Now, parallel lines!
We made a big deal last section that the
angles are created by a transversal cutting
two different lines in two different
locations.
What happens when the transversal cuts
parallel lines?
What happens is that the five named
relationships we studied now have specific
relationships.
Cutting Parallel Lines
When a transversal cuts parallel lines, the
five pairs of angles have specific
relationships.
Alternate Interior Angles (Alt Int) are
congruent.
Alternate Exterior Angles (Alt Ext) are
congruent.
Corresponding Angles (Corr) are
congruent.
Cutting Parallel Lines (Con’t)
Consecutive Interior Angles (Con Int) are
supplementary.
Consecutive Exterior Angles (Con Ext)
are supplementary.
These relations hold true ONLY if the
transversal cuts parallel lines.
If the lines are not parallel, then the
relationships don’t exist.
Example
1 2
5 6
3 4
7 8
9 10
13 14
l
< Pairs Trans Lines
11 12
15 16
n
m||n
m
p
Name
Equation
m, n
l, p
Corr
m<1 = m<9
<6 & <3
<16 & <3
l
n
Alt Int
None
p
m, n
Alt Ext
m<16 = m<3
<16 & <4
p
m, n
Con Ext
m<16+m<4=180
<1 & <9
Perpendicular Transversals
Perpendicular Transversal Theorem – In a
plane, if a line is perpendicular to one of
two parallel lines, then it is perpendicular
to the other line.
Auxiliary Line
An Auxiliary Line is a line that you can
draw any where you like. You can draw
them parallel or perpendicular or not.
30°
30°
?45°
45°
Using the
AAP, you
get m<75°
Chapter 3.3
Slopes of Lines
Slope
The slope of a line is the ratio of the
vertical rise to it’s horizontal run.
Slope = Rise
Run
m = (y2 – y1)/(x2 – x1)
Slopes can tell you if two lines are parallel
(||), perpendicular ( | ) or neither.
Slopes can not tell if two lines are
congruent or not.
Slopes of Lines
4
Create a right
triangle
2
C
3
-5
5
A
7
-2

2  (1)  3
m

3  (4) 7
Find vertical
change
Find horizontal
change
m= 3/7
Four Types of Slopes
4
Positive slope – line
going “uphill”
2
-5
5
Negative slope –
line going “downhill”
-2
Zero slope – there
is “no hill”
Undefined Slope –
there is a “wall”
Parallel vs. Perpendicular
Slopes can tell you if a pair of lines are
parallel, perpendicular or neither.
Parallel lines are lines that have the same
slope.
If the slope of one line is 3/2 and the
slope of the other line is also 3/2 then the
two lines are parallel.
Slopes of zero are parallel.
Undefined slopes are parallel.
Parallel vs. Perpendicular
For two lines to be perpendicular the slopes
have to be “opposite signed, reciprocals”.
This is pretty easy, if one line has a slope of
m = 1/3 then the slope of the perpendicular
line must be m = -3/1.
The only thing that is unusual is that if a line
has a slope of zero then the slope of the
perpendicular line is undefined.
The reverse is also true.
Chapter 3.4
Equations of Lines
Equations of Lines
There are three forms of a line equation
that you should be familiar with.
Slope Intercept Form y = mx + b.
Standard Form Ax + By = C
Point Slope Form y – y1 = m(x – x1)
It doesn’t matter which form you use, you
should be able to move from one form to
the other simply.
Slope Intercept Form
Probably the most common form of a line
equation is the Slope Intercept Form.
The reason why this is the most common
form is once you have the line equation in
this form you can simply read the slope and
the y intercept.
You have y = mx + b, where m = slope of the
line and b is the y intercept.
The coordinate of the y intercept is always
(0, b)
Standard Form
The standard form of the line equation is
Ax + By = C.
Both the x and y are on one side of the
equal sign, while the constant is on the
other side.
A, B and C are integers (no fractions or
decimals) and A must be positive.
Here you can’t just read the slope and the
y intercept, you will need to solve for them.
Point Slope Form
The point slope form may have been the
first form a linear equation that you
learned.
The equation is y – y1 = m(x – x1), where
m is the slope and the point that the slope
goes through is (x1, y1).
To use this equation you will need to plug
in m for the slope and (x1, y1) the point.
Example – Slope Intercept Form
Given a point and slope
Find the equation of a line with a slope of
2/3 through the point (3, -4)
Substitute m= 2/3, x = 3 and y = -4 into the
slope intercept form of the line equation.
You get -4 = (2/3)3 + b
Then solve for b.
b = -6
Substitute m and b back into the equation.
y = (2/3)x - 6
Example – Slope Intercept Form
Given two points
Find the equation of a line through (-3, -1)
and (6, 5)
First you need to find the slope.
m = (-1 – 5)/(-3 – 6) = -6/-9 = 2/3.
Now pick one point and do what we just did.
-1=(2/3)(-3) + b solving for b
b=1
So y=(2/3)x + 1
Another Example
Find the equation of the perpendicular line
through the line connecting (3, 5) and ( 6, -2)
through (-1, 4)
First, find the slope between the two points
m=(-2 – 5)/(6 – 3) = -7/3
Second, find the slope of the line perpendicular
to the line with a slope of -7/3, so m = 3/7
Next, solve for b: 4 = (3/7)(-1) + b, so b = 31/7
So, y = (3/7)x + 31/7 is the equation of the
perpendicular line.
Chapter 3.5
Proving Lines Parallel
Review from 3.2
If a transversal cuts parallel lines, then…
alternate interior angle pairs are congruent.
alternate exterior angle pairs are congruent.
consecutive interior angle pairs are
supplementary.
consecutive exterior angle pairs are
supplementary.
corresponding angle pairs are congruent.
Now let us work on the converses of
these statements.
Converses
If Alternate Interior Angle pairs are congruent…
If Alternate Exterior Angle pairs are congruent…
If Consecutive Interior Angle pairs are
supplementary…
If Consecutive Exterior Angle pairs are
supplementary…
If Corresponding Angle pairs are congruent..
…then the transversal intersects parallel lines.
Examples
m
n
30°
l
n & p are || - Alt Int < Thrm
30°
150°
30°
30°
30°30°
p l & m are || - Corr < Thrm
n & p are || - Alt Ext < Thrm
l & m are || - Con Int < Thrm
Another Example
3x + 12°
Find the value of x to
make these two lines
parallel.
What kind of angles are
these? Con Ext
What do Con Ext angles
x + 5°
need to be to make lines
(3x + 12) + (x + 5) = 180
parallel? Supplementary
4x + 17 = 180
4x = 163 x = 163/4
Chapter 3.6
Perpendiculars and Distance
Distance Between
a Point and a Line
The distance between a point and a line
you will need to find the length of the
perpendicular segment from the point to
that line.
Distance from a Point to a Line
D
Find the distance between:
A
B and line AD….
D and line AB
D and line CB
A and line CB
B and line CD
C
B
Distance Between Parallel Lines
To find the distance between two parallel
lines, just pick a point on one of the lines
and find the distance between the point
and a line.
Alternate definition of Parallel Lines – Coplanar
Lines that are Equidistant.
Parallel Line Theorem
In a plane, if two lines are equidistant
from a third line, then the two lines are
parallel to each other.
This is not an example of the transitive
postulate.
Example – Coordinate Geo
Find the distance from
C to line AB.
Construct a segment
perpendicular from C
to line AB.
Hint: If the line is
horizontal or vertical,
then just count the
boxes.
C
4
2
-5
5
-2
B
A
-4
So, the distance between C and line AB is 6.
Example – Coordinate Geo (H)
C
Find the distance from A
to BC.
Since BC is not Hor
D
or Vert, we need to do a
lot of work.
First, find the slope of line
B
BC. m = 3/1
Second, find equation of BC y = 3x + 13
4
2
-5
5
-2
A
-4
Third, find the perpendicular slope.
m = -1/3
Fourth, find the equation of the perpendicular line from
A to BC. y = (-1/3)x - 1
Example - Continued
So, now we have the equation of BC
y = 3x + 13 & the equation of AD y = (-1/3)x – 1.
Since both equations are written in slope
intercept form you can set them equal to each
other.
3x + 13 = (-1/3)x – 1….. mult. by 3
9x + 39 = -x – 3
10x = -42
x = - 4.2 and y = .4
Now, find the distance between A ( 3, -2) and
D ( - 4.2, 0.4)
Non-Euclidean Geometry (H)
Euclidean Geometry is what we are doing up to
this date. It is the geometry of planes.
Non-Euclidean Geometry is the geometry of
other types of systems such as spheres or
cones…..
In Spherical Geometry, we are dealing with
great circles, circles etc.
See page 165…