Download Document

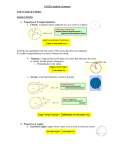
Circles
Vocabulary
And
Properties
Circle
A set of all points in a plane at a given
distance (radius) from a given point
(center) in the plane.
r

center
Radius
A segment from a point on the circle to
the center of the circle.
r

Congruent Circles
Two circles whose radii have the same measure.
r =3 cm
r =3 cm
Concentric Circles
Two or more circles that share the same center.
.

Chord
A segment whose endpoints lie on the circle.
Segments AB & CD are chords of
G
B
A
G
D
C
Diameter
A chord passing through the center of a circle.
Segment IJ is a diameter of
G
J

I
G
Secant
A line that passes through two points of the
circle.
A line that contains a chord.
Tangent
A line in the plane of the circle that intersects the
circle in exactly one point.
●

●
The point of contact is called the
Point of Tangency
Semicircle
A semicircle is an arc of a circle whose endpoints
are the endpoints of the diameter.
C
●
A

ACB is a semicircle
B
Three letters are
required to name a
semicircle: the
endpoints and one
point it passes through.
Minor Arc
An arc of a circle that is smaller than a semicircle.
C
●
P

B
Two letters are required
to name a minor arc:
the endpoints.
PC or CB are minor arcs
Major Arc
An arc of a circle that is larger than a semicircle.
C
●
A

B
ABC or CAB are major arcs
Inscribed Angle
An angle whose vertex lies on a circle and
whose sides contain chords of a circle.
A
C
B
D
<ABC & <BCD are inscribed angles
Central Angle
An angle whose vertex is the center of the circle
and sides are radii of the circle.
A

K
B
<AKB is a central angle
Properties of Circles
The measure of a central angle is two times the
measure of the inscribed angle that intercepts
the same arc.
B
A
2x
P
x
C
m<APB = 2 times m<ACB
½ m<APB = m<ACB
Example
If the m<C is 55, then the m<O is 110.
Both angle C and angle O intercept the same arc, AB.
B
A
110°
O
55°
C
Angles inscribed in the same arc are congruent.
A
The m<AQB =m<APB
both intercept arc AB.
B
Q
P
m<QAP = m<PBQ
Both angles intercept QP
Every angle inscribed in a semicircle is an
right angle.
Example
C
Each of the three
angles inscribed in
the semicircle is a
right angle.
D
B
A
E
Angle B, C, and D are all 90
degree angles.
Property #4
The opposite angles of a quadrilateral
inscribed in a circle are supplementary.
Example
The measure of angle D + angle B=180
The measure of angle C+angle A=180
B
65
A 70
115
D
110 C
Property #5
Parallel lines intercept congruent arcs on
a circle.
Example
Arc AB is congruent to Arc CD
A
B
D
C
Formulas
What are the two formulas for finding
circumference?
C=
C=
Answer
C=2 pi r
C=d pi
Area of a circle
A=?
Answer
A=radius square times pi
The End
Core-Plus Mathematics
Project Home
Math Department Home
SAHS Home