* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Circles - New Paltz Central School District
History of geometry wikipedia , lookup
Euler angles wikipedia , lookup
Lie sphere geometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Line (geometry) wikipedia , lookup
Approximations of π wikipedia , lookup
Problem of Apollonius wikipedia , lookup
Trigonometric functions wikipedia , lookup
Euclidean geometry wikipedia , lookup
History of trigonometry wikipedia , lookup
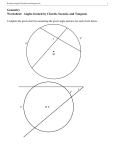
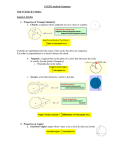
Circles Basic vocabulary History of the Circle • The circle has been known since before the beginning of recorded history. It is the basis for the wheel, which, with related inventions such as gears, makes much of modern civilization possible. In mathematics, the study of the circle has helped inspire the development of geometry and calculus. • Early science, particularly geometry and Astrology and astronomy, was connected to the divine for most medieval scholars, and many believed that there was something intrinsically "divine" or "perfect" that could be found in circles. What is a circle? • A circle is a locus of a point in a plane which moves such that its distance from a fixed point in the same plane remains constant. • The fixed point is called the center of the circle and the fixed distance is called the radius. O Here O is the center and OP is the radius. Naming a Circle Circle F F F center Use the center to name a circle. Parts of a Circle chord tangent diameter radius Segments & Lines secant Let’s review • The distance across a circle through the center is called the diameter. • Radius: is the distance from the center to any point on the circle. It is half the diameter. • Chord: A line segment linking any two points on a circle • Tangent: A line passing a circle and touching it at just one point. • Secant: A line that intersects a circle at two points. Formulas • Radius/diameter r = 1/2d and d=2r • Area A= 2 ∏r • Circumference C = 2∏r or C = ∏d Types of Arcs major arc M MNO minor arc P MO semicircle MON O N Types of Angles Central angle - Vertex is on the center. Inscribed angle - Vertex is on the circle. Circle folding activity Measure of Arcs & Angles minor arc = its central angle major arc = 360 - its central angle 68° 360 – 68 = 292 292° 68° Measure of Arcs & Angles minor arc = its central angle major arc = 360 - its central angle semicircle = 180 180° Measure of Arcs & Angles minor arc = its central angle major arc = 360 - its central angle semicircle = 180 inscribed angle = ½minor arc 68° 34° SECTOR Corresponding to a given arc, the region bounded by the two radii and the arc itself.