* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lesson
Penrose tiling wikipedia , lookup
History of geometry wikipedia , lookup
Rational trigonometry wikipedia , lookup
Multilateration wikipedia , lookup
History of trigonometry wikipedia , lookup
Integer triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
Pythagorean theorem wikipedia , lookup
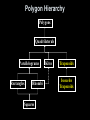
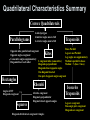
Lesson 6-6 Trapezoids and Kites 5-Minute Check on Lesson 6-5 LMNO is a rhombus. 1. Find x 2. Find y L (8y – 6)° (3x + 12)° 7 O 12 M P (5x – 2)° QRST is a square. N 3. Find n if mTQR = 8n + 8. 10.25 Q 4. Find w if QR = 5w + 4 and RS = 2(4w – 7). 5. Find QU if QS = 16t – 14 and QU = 6t + 11. 6. Standardized Test Practice: not to a rhombus? R U 6 65 T S What property applies to a square, but A Opposite sides are congruent C Diagonals bisect each other B Opposite angles are congruent D All angles are right angles Click the mouse button or press the Space Bar to display the answers. Objectives • Recognize and apply the properties of trapezoids • Solve problems involving medians of trapezoids • Apply properties of kites Vocabulary • Trapezoid – a quadrilateral with only one pair of parallel sides • Isosceles Trapezoid – a trapezoid with both legs (non parallel sides) congruent • Median – a segment that joins the midpoints of the legs of a trapezoid Polygon Hierarchy Polygons Quadrilaterals Parallelograms Rectangles Rhombi Squares Kites Trapezoids Isosceles Trapezoids Trapezoids Trapezoid Characteristics A Bases Parallel Legs are not Parallel Leg angles are supplementary (mA + mC = 180, mB + mD = 180) Median is parallel to bases Median = ½ (base + base) leg midpoint base median C ½(AB + CD) B leg midpoint D base A B Isosceles Trapezoid Characteristics Legs are congruent (AC BD) Base angle pairs congruent (A B, C D) Diagonals are congruent (AD BC) M C D Kites Characteristics A Two pairs of consecutive sides congruent AB AD and CB CD Diagonals are perpendicular AC BD D B Diagonals are angle bisectors BAC DAC and ABD CBD ADB BDC and BCA DCA Diagonal from noncongruent angles bisects other diagonal diagonal BD is cut in half Only one pair of opposite angles are congruent (the pair of angles formed by the non-congruent sides) ABC ADC C Example 1a A. If WXYZ is a kite, find mXYZ. Since a kite only has one pair of congruent angles, which are between the two non-congruent sides, WXY WZY. So, WZY = 121. mW + mX + mY + mZ = 360 Polygon Interior Angles Sum Theorem 73 + 121 + mY + 121 = 360 Substitution mY = 45 Answer: mXYZ = 45 Simplify. Example 1b B. If WXYZ is a kite, find NP. Since the diagonals of a kite are perpendicular, they divide MNPQ into four right triangles. Use the Pythagorean Theorem to find MN, the length of the hypotenuse of right ΔMNR. NR2 + MR2 = MN2 (6)2 + (8)2 = MN2 36 + 64 = MN2 100 = MN2 10 = MN Pythagorean Theorem Substitution Simplify. Add. Take the square root of each side. Answer: Since MN NP, MN = NP. By substitution, NP = 10 Example 2 The top of this work station appears to be two adjacent trapezoids. Determine if they are isosceles trapezoids. Each pair of base angles is congruent, so the legs are the same length. Answer: Both trapezoids are isosceles. Example 3 The sides of a picture frame appear to be two adjacent trapezoids. Determine if they are isosceles trapezoids. Answer: yes Example 4a DEFG is an isosceles trapezoid with median DG if and Find Theorem 8.20 Substitution Multiply each side by 2. Subtract 20 from each side. Answer: Example 4b DEFG is an isosceles trapezoid with median Find , and if and Since EF // DG, 1 and 3 are supplementary Because this is an isosceles trapezoid, 1 2 and 3 4 Substitution Combine like terms. Divide each side by 9 Answer: If x = 20, then m1 = 65° and 3 = 115°. Because 1 2 and 3 4, 2 = 65° and 4 = 115° Example 5 WXYZ is an isosceles trapezoid with median a. Answer: b. Answer: Because Quadrilateral Characteristics Summary Convex Quadrilaterals Parallelograms 4 sided polygon 4 interior angles sum to 360 4 exterior angles sum to 360 Trapezoids Bases Parallel Opposite sides parallel and congruent Legs are not Parallel Opposite angles congruent Leg angles are supplementary Consecutive angles supplementary Median is parallel to bases 2 congruent sides (consecutive) Diagonals bisect each other Median = ½ (base + base) Diagonals perpendicular Diagonals bisect opposite angles One diagonal bisected One pair of opposite angle congruent Kites Rectangles Rhombi Angles all 90° Diagonals congruent All sides congruent Diagonals perpendicular Diagonals bisect opposite angles Squares Diagonals divide into 4 congruent triangles Isosceles Trapezoids Legs are congruent Base angle pairs congruent Diagonals are congruent Summary & Homework • Summary: – In an isosceles trapezoid, both pairs of base angles are congruent and the diagonals are congruent. – The median of a trapezoid is parallel to the bases and its measure is one-half the sum of the measures of the bases • Homework: – pg 440-42; 1, 6, 7, 16-21, 41