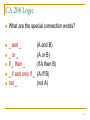* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download CA 208 Logic - DCU School of Computing
Interpretation (logic) wikipedia , lookup
Jesús Mosterín wikipedia , lookup
Combinatory logic wikipedia , lookup
Propositional calculus wikipedia , lookup
Modal logic wikipedia , lookup
Mathematical logic wikipedia , lookup
Natural deduction wikipedia , lookup
Quantum logic wikipedia , lookup
Curry–Howard correspondence wikipedia , lookup
History of logic wikipedia , lookup
Laws of Form wikipedia , lookup
CA 208 Logic
Logic
Prof. Josef van Genabith
Textbooks:
The Essence of Logic, John Kelly, Prentice Hall,
1997
Prolog Programming, Third Edition, Ivan Bratko,
Addision-Wesley, 2001
Lecture Wednesday
Tutorials/Labs Friday
1
CA 208 Logic
Course Structure
Propositional Logic
First-Order Predicate Logic
Prolog (Programming in Logic)
Assessment
50% Continuous assessment (~ week 8)
50% Final Exam
2
CA 208 Logic
Why Logic?
What is Logic used for?
Computers (Hardware/chips/CPUs etc.) are made of Logic (nand/nor
gates etc.)
You can program in Logic: Prolog (one of the main programming
paradigms:
Artificial Intelligence AI
Procedural/imperative: Basic, Fortran, Pascal, C, ...
Object oriented: C++, Java, ...
Logic: Prolog
Functional: Lisp, Miranda, Haskell, ...
Intelligence = learn and reason (Machine learning and logic)
Deep connection between abstract models of computation and
logic/proofs: Curry-Howard correspondence
Logic is foundation of maths
People use logic ...
…
3
CA 208 Logic
Logic
Today:
Intuitions ...
Jargon ...
If you get these right, Logic is easy!!!
Formalisation comes after intuitions ...!
Not so well covered in the text books
4
CA 208 Logic
What is logic?
Logic is the science of reasoning / inferencing
/ drawing conclusions
We do this all the time ...
What is involved in reasoning?
Premises and Conclusions
Premises: what you hold to be true
Conclusions: what you derive from the
premises
5
CA 208 Logic
An example:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
We say that “P entails C”, “C logically follows from
P”, “C is derived from P”, “C is inferred from P”, etc.
We write “P |= C” or “P|- C” ((double) turnstile)
6
CA 208 Logic
An example:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
There are many types of Logic ...
Classical Logic, intuitionistic logic, linear logic, nonmonotonic logic, defeasible logic, fuzzy logic, ...
There is a whole zoo of logics!
7
CA 208 Logic
An example:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
There are many types of Logic ...
In this course we look at classical Logic(s) only !
(In AI, KR you may come across some of the other
logics).
8
CA 208 Logic
An example:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
What is classical Logic?
Classical Logic studies/characterises/defines valid
reasoning
Valid reasoning is a very strict type of reasoning
where truth of the premises guarantees truth of the
conclusions (if you use the rules of classical logic to
do the reasoning, i.e. to derive the conclusion!)
9
CA 208 Logic
An example:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
Our example is a valid inference! Why?
Well, if the premisses are true, then the conclusion
is true
In other words: it cannot be the case that all the
premisses are true and the conclusion is false
10
CA 208 Logic
An example:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
Our example is a valid inference! Why?
In all the situations where the premisses are true,
the conclusion is true as well
In other words: it cannot be the case that there is a
situation where all the premisses are true and the
conclusion is false
11
CA 208 Logic
Another example:
P: If John goes to the party then Mary goes to the
party. Mary goes to the party.
C: John goes to the party.
Is this a valid inference? I.e. does truth of premisses
guarantee truth of conclusion?
Can you come up with a situation where P is true
and C is false?
?
12
CA 208 Logic
Another example:
P: If John goes to the party then Mary goes to the
party. Mary goes to the party.
C: John goes to the party.
Is this a valid inference? I.e. does truth of premisses
guarantee truth of conclusion?
Can you come up with a situation where P is true
and C is false?
Yes ... !!!!
13
CA 208 Logic
Formalisation:
P: If John goes to the party then Mary goes to the party. John goes
to the party.
C: Mary goes to the party.
Logicians (like mathematicians, computer
scientists/programmers, engineers) are lazy ...
They don’t like to write very much ...
They like abstraction and generalisation ...
They don’t like specific cases ...
So how do they/can we generalise this logic stuff??
We express that reasoning stuff as formulas ;-)
14
CA 208 Logic
Formalisation:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
Premisses and conclusions are made up of complex
and elementary “propositions” or ”statements”
What are propositions/statements? Sentences that
are true or false
15
CA 208 Logic
Formalisation:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
16
CA 208 Logic
Formalisation:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
17
CA 208 Logic
Formalisation:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
18
CA 208 Logic
Formalisation:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
19
CA 208 Logic
Formalisation:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
20
CA 208 Logic
Formalisation:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
How: look at the components of the premisses and
conclusion
Special symbols (if __ then __ )
Component propositions/statements:
John goes to the party = A
Mary goes to the party = B
21
CA 208 Logic
Formalisation:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
P: {If A then B , A}
C: B
A = John goes to the party
B = Mary goes to the party
22
CA 208 Logic
Formalisation:
P: If John goes to the party then Mary goes to the
party. John goes to the party.
C: Mary goes to the party.
P: {If A then B , A}
C: B
P |= C
{If A then B , A} |= B
A = John goes to the party
B = Mary goes to the party
23
CA 208 Logic
And now sth. absolutely amazing happens:
P: {If A then B , A}
C: B
A = John goes to the party, B = Mary goes to the party
A = Kate is a CA2 student, B = Kate does Logic
P: If Kate is a CA2 student, then Kate does Logic. Kate is a CA2
student.
C: Kate does Logic.
Is that a valid inference?
24
CA 208 Logic
And now sth. absolutely amazing happens:
P: {If A then B , A}
C: B
A = John goes to the party, B = Mary goes to the party
A = Kate is a CA2 student, B = Kate does Logic
P: If Kate is a CA2 student, then Kate does Logic. Kate is a CA2
student.
C: Kate does Logic.
Is that a valid inference? YES!!!!
25
CA 208 Logic
And now sth. amazing happens:
P: {If A then B , A}
C: B
A = John goes to the party, B = Mary goes to the party
A = Kate is a CA2 student, B = Kate does Logic
You get another valid inference! In fact you get loads of valid
inferences from the abstract {If A then B , A} |- B schema above
by replacing the propositional variables with actual propositions
...
The old Greeks copped on to that some 2500 years ago ...
Aristotle, rules/mathematics of inference, syllogisms, ..., rules
that guarantee that if you apply them to true premises you get
true conclusions !!! (Aside the Greeks didn’t get all of them right)
26
CA 208 Logic
And now another amazing thing happens:
Logic is not just about the “real” world! You can consider premises that
are not true in real world:
P: {If A then B , A}
C: B
A = Kate is a CA2 student, B = Kate does Formal Languages
P: If Kate is a CA2 student, then Kate does Formal Languages. Kate is a
CA2 student.
C: Kate does Formal Languages.
P |- C, i.e. this is a vaild inference but: but C not true in “real” world.
Kate could be CAIS student!
So Logic allows us to explore hypothetical scenarios: for the sake of the
inference, imagine situations where all of the premises in P are true ...
27
CA 208 Logic
Another example ...
P: John likes soccer and John likes Kate.
C: John likes Kate.
Is that vaild? Formalise:
P: { A and B }
C: B
P |- C
{ A and B } |- B
Another one ...
A = Kate is a student, B = Kate likes the bar
What about { A and B } |- A ? Is that valid?
28
CA 208 Logic
Another example ...
P: John likes soccer. John likes Kate.
C: John likes soccer and John likes Kate.
Formalise:
P: { A , B }
C: A and B
P |- C
{ A , B } |- A and B
A = Kate is a student, B = Kate likes the bar
What about { A , B } |- B and A ? Is that valid?
29
CA 208 Logic
What are propositions/statements?
Statements/Propositions are sentences that are either true or false!
John likes soccer.
Kate is a CA student.
Not all sentences are propositions/statements:
Questions/Interrogatives:
Is Kate a CA student?
Commands/Imperatives:
Give John a copy of the exam!
Classical logic is only about statements/propositions!!!
The only thing you can have in the premises and conclusions are
statements and special connection words (like if _ then _, and ..)
30
CA 208 Logic
What are the special connection words?
_ and _
_ or _
if _ then _
_ if and only if _
not _
(A and B)
(A or B)
(if A then B)
(A iff B)
(not A)
31
CA 208 Logic
You have seen this before: Logicians are lazy ...
A and B
AB
A or B
AB
if A then B
AB
(P implies Q)
A iff B
AB
not A
A
Note that different books may use different symbols,
e.g. & for , for and the like ...
That is just to confuse you ...
32
CA 208 Logic
So with this we can write
{A B , A} |- B
{A B } |- A
{A B } |- B
{A , B} |- A B
And the like ...
33
CA 208 Logic
What is the “meaning” of the logical connectives
?
We’ll define the meaning of the connectives in two
ways:
Truth tables (Semantics, |= )
Proofs (Syntax, |- )
Meaning of the logical connectives is not exactly like
the meaning of not, and, or, implies etc. in English
(natural language) ... We’ll see examples of that!
34
CA 208 Logic
What’s a truth table?
A truth table shows all possible situations in which the proposional arguments of
a logical connective are true or false and defines the truth value of the complex
proposition in terms of these.
Intutively the complex proposition
John likes football and Mary likes the bar
is true in all situations where ‘John likes football’ is true and where ‘Mary likes
the bar’ is true, and false in all other situations.
P Q is true in all situations where P is true and where Q is true, and false in all
other situations.
There can be infinitely many situations in which P, Q are true – we don’t want to
look at all of them ...!
Truth tables cluster them together and capture what is essential about them.
35
CA 208 Logic
We capture this in a
truth table.
We write ‘1’ for true and
‘0’ for false (or T, F)
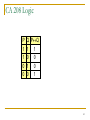
Truth table for
P Q PQ
1 1
1 0
0 1
0 0
36
CA 208 Logic
We capture this in a
truth table.
We write ‘1’ for true and
‘0’ for false (or T, F)
Truth table for
P Q PQ
1 1
1
1 0
0
0 1
0
0 0
0
37
CA 208 Logic
Question:
Is PQ = QP ?
Logical equivalence, same
meaning
Use truth table ...
P Q PQ
1 1
1
1 0
0
0 1
0
0 0
0
QP
38
CA 208 Logic
Question:
Is PQ = QP ?
Logical equivalence, same
meaning
Use truth table ...
Hence PQ = QP
We say that PQ and QP are
logically equivalent, i.e. They
have the same truth value (i.e.
meaning) under each
interpretation (situation)
We write (PQ) (QP)
Temporal aspect of natural
language ‘and’ ...
P Q PQ
QP
1 1
1
1
1 0
0
0
0 1
0
0
0 0
0
0
39
CA 208 Logic
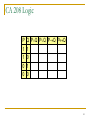
P
1
1
0
0
Q PQ
1 1
0 1
1 1
0 0
P Q PQ QP
1 1
1
1
1 0
1
1
0 1
1
1
0 0
0
0
• Sometimes exclusive aspect of meaning of natural language ‘or’ ...
• Logical or is inclusive ...
40
CA 208 Logic
P
1
1
0
0
Q PQ
1
1
0
0
1
1
0
1
P Q PQ QP
1 1
1
1
1 0
0
1
0 1
1
0
0 0
1
1
• Natural language implication has often element of causality ...
• Logical implication doesn’t ... !!!!
41
CA 208 Logic
P
1
1
0
0
Q PQ
1
1
0
0
1
0
0
1
42
CA 208 Logic
P
1
1
0
0
Q PQ PQ PQ PQ
1
0
1
0
43
CA 208 Logic
P
1
1
0
0
Q PQ PQ PQ PQ
1 1
0 0
1 0
0 0
44
CA 208 Logic
P
1
1
0
0
Q PQ PQ PQ PQ
1 1
1
0 0
1
1 0
1
0 0
0
45
CA 208 Logic
P
1
1
0
0
Q PQ PQ PQ PQ
1 1
1
1
0 0
1
0
1 0
1
1
0 0
0
1
46
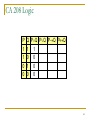
CA 208 Logic
P
1
1
0
0
Q PQ PQ PQ PQ
1 1
1
1
1
0 0
1
0
0
1 0
1
1
0
0 0
0
1
1
47
CA 208 Logic
P P
1 0
0 1
P P P
1 0
0 1
1
0
48
CA 208 Logic
P
1
1
0
0
Q PQ PQ PQ PQ
1 1
1
1
1
0 0
1
0
0
1 0
1
1
0
0 0
0
1
1
49
CA 208 Logic
A (Boolean) algebra of Logic
Commutativity
Associativity
Distributivity
Idempotency
P Q
Absorption
1 1
...
PQ
PQ
PQ
PQ
1
1
1
1
1
0
0
1
0
0
0
1
0
1
1
0
0
0
0
0
1
1
50