* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Training - NUS Business School
Survey
Document related concepts
Transcript
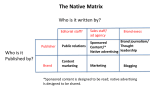
An Extreme Value Reference Price Approach Sanjoy Ghose and Oded Lowengart January 19, 2005 1 Effect of Price on Choice Price Only models Inclusion of Reference Price 2 Reference Price Categories External Reference Price Internal Reference Price 3 Internal Reference Prices Many different operationalizations Issue of appropriateness 4 Logic & Forms Decaying memory of past occurrences Last Price paid (Winer, 1986; Mayhew & Winer, 1992) Variation of past average prices – Weighted log-mean average (Kalwani et al., 1990) – Exponentially weighted average (Obermiller, 1990) 5 Event Recall Hastie’s theory on memory Srull’s experiments Incongruence vs Congruence of Information Effect on recall 6 Price & Information Congruence Let Pexp = Expected price of consumers Let price at time t = Pt If Pt is similar to Pexp then Pt is congruent information 7 If Pt >> (or <<) than Pexp, then Pt is incongruent information Price & Information Congruence The greater the degree of deviation of Pt from Pexp, the greater the incongruency of information. The greatest incongruency should occur with the maximum and minimum prices faced by consumers from t=0 to t=t. 8 Price & Information Congruence Such maximum and minimum prices should be most easily recalled We hypothesize that these prices would be used as reference points in price evaluations. 9 Other Related Literature Monroe (1979) Range Theory (Volkmann, 1951) – Applications to Pricing in the Mktg. lit. Experimental studies Janiszewski and Lichtenstein, 1999 Niedrich, Sharma, and Wedell, 2001 – price attractiveness recommends that it was important for future research to consider range in the operationalization of reference prices in choice models. 10 Let V be the Utility V X Y (1) where X - gain Y - loss and - parameters, Similar to Rajendran & Tellis (1994).. 11 X PMax PAct (2) Y PAct PMin (3) Substituting (2) and (3) into (1), V ( PMax PAct ) ( PAct PMin ) PMax PMin ( ) PAct V 1PMax 2 PMin 3 PAct Where, 12 1 2 3 (4) Extreme Values of Reference Price 13 Consumers would utilize the maximum and minimum prices they have paid in their previous shopping trips as reference prices. This should be reflected in superior performance of a model based on the EVRP approach. Range Theory A stimulus range is based on its extreme points Relative judgment and anchoring effects Human Association Memory A new incongruent stimulus leads to a larger associative memory network Different memory retrieval for Incongruent information Anchoring Points - Product Line A new extreme stimulus is more noticeable than other stimulus Behavioral Theory Individuals can be happy and sad at the same time Price Implications A price range is related to the extreme price levels Price attractiveness is relative to the extreme prices New extreme prices change the range Price Implications A new extreme (high/low) price has more memory associations than an expected new price New extreme prices retrieved better from memory than regular prices Price Implications A new extreme (maximum/minimum) price is more noticeable Price Implications Both maximum and minimum prices can be simultaneously used in evaluating new prices Internal Reference Price Conceptualization Consumers use both high and low extreme points (price) in their evaluations of a new price at the same time Consumers can recall better extreme values (price) as compared with regular prices (expected) they paid previously Consumers use extreme points (price) to decide about the attractiveness of the offer Consumers use maximum and minimum prices as anchoring Choice/Purchase Quantity Implications: Focus of the Current Research Consumers use two internal reference prices to evaluate current price - comparing current price against the two, simultaneously in a brand choice/purchase quantity situation A maximum paid price - high anchoring - creates gains A minimum paid price - low anchoring - creates losses Theoretical Framework 14 Hypotheses 15 1) For the aggregate sample, the EVRP approach for modeling consumer choice can serve as a better representation of internal reference price as compared to a last price paid formulation. Hypotheses 16 2) For the aggregate sample, the EVRP approach for modeling consumer choice can serve as a better representation of internal reference price as compared to an average price paid formulation. EVRP & Segments Ratio of incongruent & congruent Info (Srull, 1981) Number of price points faced by consumer Purchase frequency 17 Hypotheses 3) The EVRP approach for modeling consumer choice can serve as a better representation of internal reference price in the high frequency segment than in the low frequency segment. 18 Hypotheses 4) For each of the two buyer frequency segments, the EVRP approach for modeling consumer choice can serve as a better representation of internal reference price as compared to a last price paid formulation. 19 Hypotheses 20 5) For each of the two buyer frequency segments, the EVRP approach for modeling consumers’ choice can serve as a better representation of internal reference price as compared to an average price paid formulation. Gains & Losses Consumers evaluate losses & gains differently (Kahneman & Tversky, 1979) We believe: On any given purchase occasion, a consumer is always evaluating a loss as well as a gain 21 Model Pijt exp j m j 1 (U ijt ) exp (U ijt ) U ijt Vijt ijt 22 gain ( Pmax Pact ) loss ( Pact Pmin ) EVRP Model Vijt j 2 Pijtmax gain 3 Pijtmin loss 4 DISPijt 5 FEATijt 6 LOYijt 23 LPP Model Vijt j 2 Pijtlast gain1 3 Pijtlastloss 2 4 DISPijt 5 FEATijt 6 LOYijt 1 if ( pijtr Pijto ) 0 1 0 otherwise 1 if ( pijtr Pijto ) 0 2 0 otherwise 24 APP Model Vijt j P P average gain 2 ijt 1 5 FEATijt 6 LOYijt 1 if ( pijtr Pijto ) 0 1 0 otherwise 1 if ( pijtr Pijto ) 0 2 0 otherwise 25 2 4 DISPijt averageloss 3 ijt Data A.C. Nielsen company scanner panel data set of laundry detergents: Sioux Falls market Seven leading brands of liquid detergents Tide 128 oz, Tide 96 oz, Tide 64 oz, Wisk 64 oz, Wisk 32 oz, Surf 64 oz, and Surf 32 oz. 26 Variables Minimum Price - the lowest price paid or observed by consumer i for choice alternative j in previous purchase occasions Maximum Price - the highest price paid or observed by consumer i for choice alternative j in previous purchase occasions 27 Description of Conceptual Approach Price Subject Node 5.95 Max.... 5.12 4.56 4.50 t=1 28 4.12 3.95 Min... t=2 5.95 ... Max t=3 3.24 t=4 3.95 4.01 t=5 3.12 t=6 t=7 3.12 ... Min t=8 t=9 t=10 Time Table 1: MNL Results: Calibration Sample – Aggregate Level Variable Display Feature Brand Specific 1 Brand Specific 2 Brand Specific 3 Brand Specific 4 Brand Specific 5 Brand Specific 6 Loyalty Gain Loss 29 Average Price Last Price EVRP Coefficient P-value Coefficient P-value Coefficient P-value 0.0000 1.4731 0.0000 1.3764 0.0000 1.5604 0.0001 1.3164 0.0000 1.4759 0.0000 1.3903 0.9266 -0.2640 0.4860 0.0314 -1.2466 0.0166 0.0307 0.6785 0.0024 0.9091 0.8742 0.0585 0.2009 0.3885 0.0842 0.5174 0.4101 0.2505 -0.0421 0.9197 -0.1910 0.6461 -0.1359 0.7432 -1.3287 0.0073 -0.2411 0.5401 -0.4777 0.2361 0.6352 0.1411 0.5331 0.1857 -0.4006 0.2438 0.0000 3.7359 0.0000 3.7921 0.0000 3.6325 0.0035 0.0104 0.0900 0.0039 0.0088 0.0071 0.1042 -0.0042 0.2857 0.0041 -0.0116 0.0000 Results EVRP model: Significant gain and loss parameters Losses loom larger than gains; consistent with Prospect Theory Less face validity for LPP and APP models especially for loss parameters 30 Table 2: Goodness-of-Fit Measurements - Aggregate Level - Calibration Sample Goodness of-fit Measures Log Likelihood BIC AIC CAIC 31 EVRP -299.747 657.211 632.494 668.211 Last Price Average Price -304.631 -304.744 666.979 667.205 642.262 642.488 677.979 678.205 Results EVRP model provides superior fit based on the four different measures in Table 2 Supporting hypotheses 1 and 2 32 Table 3: Accuracy of Model Prediction -Aggregate Level - Hold-Out Sample Prediction Hit-rate 33 EVRP 60% Last Price 57% Average Price 57% Results EVRP gave better hit rate predictions than LPP or APP Superiority similar to other works in marketing literature (e.g., Manchanda et al, 1999 Mktg Sci; Heilman et al., 2000 JMR) Further support to hypotheses 1 & 2 34 Segmentation To test hypotheses 3 to 5 High & low frequency of purchase Checked segmentation scheme – LL test (Gensch, 1985) 35 Table 4: Log-Likelihood Tests – Calibration Segmented Sample LL - Aggregate Model LL - High Frequency Segment LL - Low Frequency Segment 2LL 36 EVRP -299.747 -154.921 -132.357 24.938 Last Price -304.631 -156.354 -134.949 26.656 Average Price -304.744 -157.266 -133.933 27.09 Table 5: MNL Results: High Frequency Purchasing Segment – Calibration Sample Variable Display Feature Brand Specific 1 Brand Specific 2 Brand Specific 3 Brand Specific 4 Brand Specific 5 Brand Specific 6 Loyalty Gain Loss 37 EVRP Last Price Average Price Coefficient P-value Coefficient P-value Coefficient P-value 1.9515 0.0000 1.6565 0.0001 1.8172 0.0000 0.5902 0.2342 0.7056 0.1564 0.5543 0.2618 -1.9329 0.0251 -0.3585 0.4614 -0.4456 0.3994 -0.2606 0.6540 0.7627 0.0680 0.6521 0.1395 -0.2882 0.5201 0.0152 0.9725 -0.0766 0.8641 -0.4890 0.4335 -0.7288 0.2417 -0.6676 0.2842 -2.6480 0.0075 -1.2865 0.1104 -1.4208 0.0797 -1.1091 0.0528 -0.2956 0.5137 -0.3252 0.4748 4.3960 0.0000 4.5246 0.0000 4.5814 0.0000 0.0082 0.0627 0.0023 0.4919 0.0074 0.1340 -0.0124 0.0080 0.0065 0.0826 0.0013 0.8041 Table 6: MNL Results: Low Frequency Purchasing Segment – Calibration Sample Variable Display Feature Brand Specific 1 Brand Specific 2 Brand Specific 3 Brand Specific 4 Brand Specific 5 Brand Specific 6 Loyalty Gain Loss 38 EVRP Last Price Average Price Coefficient P-value Coefficient P-value Coefficient P-value 1.4134 0.0042 1.3351 0.0061 1.3637 0.0057 2.0136 0.0000 2.0959 0.0000 1.9276 0.0001 -1.1673 0.0915 -0.2675 0.6090 -0.6461 0.2693 -0.5750 0.2896 0.0464 0.9252 -0.1801 0.7185 0.2544 0.5588 0.5032 0.2348 0.3764 0.3796 0.0724 0.8934 0.0407 0.9398 0.0671 0.9014 -0.7790 0.1800 -0.0570 0.9064 -0.2988 0.5530 -0.2420 0.5705 0.1104 0.7849 0.0731 0.8560 2.8825 0.0000 3.0463 0.0000 2.9667 0.0000 0.0063 0.0990 0.0064 0.0596 -0.0078 0.2266 -0.0108 0.0029 0.0005 0.8956 0.0142 0.0107 Segment level findings: Tables 5 and 6 EVRP: parameter signs are generally consistent with expectations – losses loom larger than gains – model has face validity signs & significances of gain & loss parameters show less face validity for LPP and APP models. 39 Table 7: Goodness-of-Fit Measurements - Disaggregate Level - Calibration Period Goodness of-fit Measures High Frequency Segment LL BIC AIC CAIC Low Frequency Segment LL BIC AIC CAIC 40 EVRP Last Price Average Price -154.921 366.779 342.842 377.779 -156.354 369.645 345.708 380.645 -157.266 371.469 347.532 382.469 -132.357 316.908 297.714 327.908 -134.949 322.092 302.898 333.092 -133.933 320.060 300.866 331.060 Table 8: Accuracy of Model Predictions – Hold-Out Segmented Sample High Frequency Segment Hit-rate Low Frequency Segment Hit Rate 41 EVRP Last Price Average Price 65% 62% 61% 56% 51% 52% Segment level findings EVRP has the best fit (Table 7) Also has the best holdout sample predictive accuracy (Table 8) True for both high purchase frequency and low purchase frequency segments Supports hypotheses 4 and 5 42 Results EVRP (High Freq. Segment): McFadden’s R-sq. = .550 and Hit Rate = 65% EVRP (Low Freq. Segment): McFadden’s R-sq. = .408 and Hit Rate = 56% EVRP provides better data representation for high vs low freq segment; Supports Hypothesis 3 43 Quantity Analysis Table 9: Regression Results – Aggregate Level Special display Feature Gain Loss 44 Estimated Parameter 7.645 0.094 0.287 -0.262 P-value 0.0290 0.9781 0.0000 0.0000 Quantity Analysis Table 10: Regression Results – High Frequency Purchasing Segment Special display Feature Gain Loss 45 Estimated Parameter 6.122 -3.722 0.196 -0.250 P-value 0.2518 0.5231 0.0000 0.0000 Quantity Analysis Table 11: Regression Results – Low Frequency Purchasing Segment Special display Feature Gain Loss 46 Estimated Parameter 8.844 2.315 0.327 -0.261 P-value 0.0657 0.6096 0.0000 0.0000 Results Extreme value points model consistent with expectations both gains and losses are statistically significant A larger effect for gains than losses for the low frequency segment The high frequency segment show a larger effect for losses than gains 47 Summary Reference Price based choice models have always done better than priceonly models Internal Reference Price models have been mainly driven by the decaying memory concept 48 Summary Instead, incorporating the incongruency of information approach together with the range theory concept Recent work (2001) suggest the attractiveness of range theory approach for price attractiveness judgments 49 Summary Niedrich et al (2001) say it is important to consider range in the operationalization of choice models EVRP --- a first step in that direction 50 Summary Past studies on Internal reference price --- either a gain or a loss on a given purchase occasion Our concept: consumers maybe experiencing a gain and a loss on each purchase occasion 51 Managerial Implications While a price promotion strategy might have a short-run positive impact on sales, the lowered price may result in the installation of a new lower minimum price in consumers' memories – may lead to a negative effect on market shares in the medium and long terms 52 Managers may want to consider non-price forms for promotion if the goal is to increase short-term sales Managerial Implications While a price increase may have an immediate adverse effect on sales, the possible higher maximum price level can help future market share values in the form of positive effect of gains Similar logic for choice of skimming vs. penetration strategies for new product introductions. 53 54