Download GENETICS – BIO 300

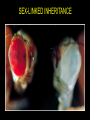
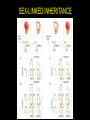
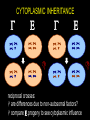
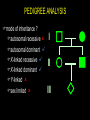
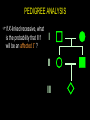
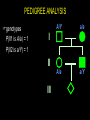
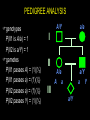
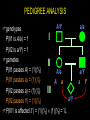
LECTURE 03: PATTERNS OF INHERITANCE II
genetic ratios & rules
statistics
binomial expansion
Poisson distribution
sex-linked inheritance
cytoplasmic inheritance
pedigree analysis
GENETIC RATIOS AND RULES
product rule: the probability
of independent events
occurring together is the
product of the probabilities of
the individual events... AND
A/a x A/a
½ A+ ½ a  ½ A+ ½ a
P(a/a) = ½ x ½ = ¼
sum rule: the probability of
A/a x A/a
either of two mutually
½ A+ ½ a  ½ A+ ½ a
exclusive events occurring is
P(A/a) = ¼ + ¼ = ½
the sum of the probabilities of
the individual events... OR
STATISTICS: BINOMIAL EXPANSION
diploid genetic data suited to analysis (2 alleles/gene)
examples... coin flipping
product and sum rules apply
n
 use formula: (p+q)n =  [n!/(n-k)!k!] (pn-kqk) = 1
k=0
 define symbols...
STATISTICS: BINOMIAL EXPANSION
n
 use formula: (p+q)n =  [n!/k!(n-k)!] (pkqn-k) = 1
k=0
 define symbols...
 p = probability of 1 outcome, e.g., P(heads)
 q = probability of the other outcome, e.g.,
P(tails)
 n = number of samples, e.g. coin tosses
 k = number of heads
 n-k = number of tails
  = sum probabilities of combinations in all
STATISTICS: BINOMIAL EXPANSION
n
 use formula: (p+q)n =  [n!/k!(n-k)!] (pkqn-k) =
1
k=0
 e.g., outcomes from monohybrid
cross...
 p = P(A_) = 3/4, q = P(aa) = 1/4
 k = #A_, n-k = #aa
 2 possible outcomes if n = 1:
k = 1, n-k = 0 or k = 0, n-k = 1
 3 possible outcomes if n = 2:
k = 2, n-k = 0 or k = 1, n-k = 1 or k = 0, n-k = 2
 4 possible outcomes if n = 3... etc.
STATISTICS: BINOMIAL EXPANSION
n
 use formula: (p+q)n =  [n!/k!(n-k)!] (pkqn-k) =
1
k=0
 e.g., outcomes from monohybrid
cross...
1 offspring, n = 1,
(p+q)1 = 1
2 offspring, n = 2,
(p+q)2 = 1
3 offspring, n = 3,
(p+q)3 = 1
(1!/1!0!)(¾)1(¼)0 = 3/4
(1!/0!1!)(¾)0(¼)1 = 1/4
 = 1
(2!/2!0!)(¾)2(¼)0 = (1)9/16
(2!/1!1!)(¾)1(¼)1 = (2)3/16
(2!/0!2!)(¾)0(¼)2 = (1)1/16
 = 1
16/16
(3!/3!0!)(¾)3(¼)0 = (1)27/64
(3!/2!1!)(¾)2(¼)1 = (3)9/64  P of 2A_ + 1aa
(3!/1!2!)(¾)1(¼)2 = (3)3/64
(3!/0!3!)(¾)0(¼)3 = (1)1/16
 = 1
STATISTICS: BINOMIAL EXPANSION
Q: True breeding black and albino cats have a litter of
all black kittens. If these kittens grow up and breed
among themselves, what is the probability that at least
two of three F2 kittens will be albino?
A: First, define symbols and sort out basic genetics...
one character – black > albino, one gene B > b ...
STATISTICS: BINOMIAL EXPANSION
P1:
genotype:
gametes:
black
BB
P(B) = 1
×

albino
bb
P(b) = 1
F1:
genotype:
gametes:
black
Bb
P(B) = ½ , P(b) = ½
×

black
Bb
P(B) = ½ , P(b) = ½
expected F2:
P(black) = P(B_) = (½ )2 + 2(½ )2 = ¾ = p
P(albino) = P(bb) = (½ )2 = ¼ = q
STATISTICS: BINOMIAL EXPANSION
possible outcomes for three kittens...
F2
*
3 black + 0 albino

P (   ) = (¾ )3 × (¼ )0 = 27/64

P (   ) = (¾ )2 × (¼ )1 = 9/64
P (   ) = (¾ )2 × (¼ )1 = 9/64
P (   ) = (¾ )2 × (¼ )1 = 9/64
1 black + 2 albino

P (   ) = (¾ )1 × (¼ )2 = 3/64
P (   ) = (¾ )1 × (¼ )2 = 3/64
P (   ) = (¾ )1 × (¼ )2 = 3/64
0 black + 3 albino

P (   ) = (¾ )0 + (¼ )3 = 1/64
2 black + 1 albino
Total
Probability
64/64
STATISTICS: PASCAL’S TRIANGLE
Sample Frequency
Possible Outcomes*
Combinations
1×
1+1
2 orders

2×
1+2+1
3 orders
 
3×
4 orders
+++
  
4×
1+4+6+4+1
5 orders
   
5×
1 + 5 + 10 + 10 + 5 + 1

6×



6 orders

1 + 6 + 15 + 20 + 15 + 6 + 1
7 orders
STATISTICS: BINOMIAL EXPANSION
n
 expansion of (p+q)n =  [n!/k!(n-k)!] (pkqn-k) = 1
k=0
... if p(black) = ¾, q(albino) = ¼, n = 3 ...
expansion of (p+q)3 = (¾+¼)(¾+¼)(¾+¼ ) =
(3!/3!0!) (¾)3(¼)0 =  x 27/64 = 27/64 = P(0 albinos)
(3!/2!1!) (¾)2(¼)1 =  x 9/64 = 27/64 = P(1 albino)
(3!/1!2!) (¾)1(¼)2 =  x 3/64 = 9/64 = P(2 albinos)
(3!/0!3!) (¾)0(¼)3 =  x 1/64 = 1/64 = P(3 albinos)
P(at least 2 albinos) = 9/64 + 1/64 = 5/32
}
SEX-LINKED INHERITANCE
SEX-LINKED INHERITANCE
 are homogametic
 are heterogametic
SEX-LINKED INHERITANCE
SEX-LINKED INHERITANCE
SEX-LINKED INHERITANCE
SEX-LINKED INHERITANCE
 all red
 all white
SEX-LINKED INHERITANCE
 all red
 red and white
the white gene is X-linked
CYTOPLASMIC INHERITANCE






selfing:
 are there differences between groups?
 are they true-breeding “genotypes”?
CYTOPLASMIC INHERITANCE







reciprocal crosses:
 are differences due to non-autosomal factors?
 compare  progeny to see cytoplasmic influence

STATISTICS: POISSON DISTRIBUTION
binomial... sample size (n)  10 or 15 at most
if n = 103 or even 106 need to use Poisson
e.g. if 1 out of 1000 are albinos [P(albino) = 0.001],
and 100 individuals are drawn at random, what are the
probabilities that there will be 3 albinos ?
formula: P(k) = e-np(np)k
k!
STATISTICS: POISSON DISTRIBUTION
 formula:
P(k) = e-np(np)k
k!
 k (the number of rare events)
 e = natural log =  (1/1! + 1/2! + … 1/!) =
2.71828…
 n = 100
 p = P(albino) = 0.001
 np = P(albinos in population) = 0.1
 P(3) = e–0.1(0.1)3/3! = 2.718–0.1(0.001)/6 = 1.5 × 10–4
PEDIGREE ANALYSIS
pedigree analysis is the starting point for all
subsequent studies of genetic conditions in families
main method of genetic study in human lineages
at least eight types of single-gene inheritance can be
analyzed in human pedigrees
goals
identify mode of inheritance of phenotype
identify or predict genotypes and phenotypes of all
individuals in the pedigree
... in addition to what ever the question asks
PEDIGREE ANALYSIS: SYMBOLS
PEDIGREE ANALYSIS
 order of events for solving pedigrees
1. identify all individuals according number and letter
2. identify individuals according to phenotypes and
genotypes where possible
3. for I generation, determine probability of genotypes
4. for I generation, determine probability of passing allele
5. for II generation, determine probability of inheriting
allele
6. for II generation, same as 3
7. for II generation, same as 4… etc to finish pedigree
PEDIGREE ANALYSIS
 additional rules...
1. unaffected individuals mating into a pedigree are
assumed to not be carriers
2. always assume the most likely / simple explanation,
unless you cannot solve the pedigree, then try the
next most likely explanation
PEDIGREE ANALYSIS
Autosomal Recessive: Both sexes affected; unaffected
parents can have affected progeny; two affected
parents have only affected progeny; trait often skips
generations.
PEDIGREE ANALYSIS
Autosomal Dominant: Both sexes affected; two
unaffected parents cannot have affected progeny;
trait does not skip generations.
PEDIGREE ANALYSIS
X-Linked Recessive: More  affected than ; affected 
pass trait to all ; affected  cannot pass trait to ;
affected  may be produced by normal carrier  and
normal .
PEDIGREE ANALYSIS
X-Linked Dominant: More  affected than ; affected 
pass trait to all  but not to ; unaffected parents
cannot have affected progeny.
PEDIGREE ANALYSIS
Y-Linked: Affected  pass trait to all ;  not affected
and not carriers.
Sex-Limited: Traits found in  or in  only.
Sex-Influenced,  Dominant: More  affected than ; all
daughters of affected  are affected; unaffected
parents cannot have an affected .
Sex-Influenced,  Dominant: More  affected than ; all
sons of an affected  are affected; unaffected
parents cannot have an affected .
PEDIGREE ANALYSIS
mode of inheritance ?
autosomal recessive 
autosomal dominant 
X-linked recessive 
X-linked dominant 
Y-linked 
sex limited 
I


II


III

PEDIGREE ANALYSIS
if X-linked recessive, what
is the probability that III1
will be an affected  ?
I


II


III

PEDIGREE ANALYSIS
genotypes
P(II1 is A/a) = 1
P(II2 is a/Y) = 1
A/Y
a/a
I


II

A/a

a/Y
III

PEDIGREE ANALYSIS
genotypes
P(II1 is A/a) = 1
P(II2 is a/Y) = 1
gametes
P(II1 passes A) = (1)(½)
P(II1 passes a) = (1)(½)
P(II2 passes a) = (1)(½)
P(II2 passes Y) = (1)(½)
A/Y
a/a
I


II

A/a

a/Y
III
A
a

a/Y
a
Y
PEDIGREE ANALYSIS
A/Y
genotypes
I
P(II1 is A/a) = 1
P(II2 is a/Y) = 1
gametes
II
P(II1 passes A) = (1)(½)
A/a
P(II1 passes a) = (1)(½)
A a
III
P(II2 passes a) = (1)(½)
a/Y
P(II2 passes Y) = (1)(½)
P(III1 is affected ) = (1)(½)  (1)(½) = ¼
a/a




a/Y

a
Y
PATTERNS OF INHERITANCE: PROBLEMS
in Griffiths chapter 2, beginning on page 62, you should
be able to do ALL of the questions
begin with the solved problems on page 59 if you are
having difficulty
check out the CD, especially the pedigree problems
try Schaum’s Outline questions in chapter 2, beginning
on page 66, and chapter 5, beginning on page 158