Download Chapter 5 Work, Power and Energy

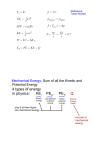
Chapter 5
Work, Power and
Energy
Work


Provides a link between force and
energy
The work, W, done by a constant
force on an object is the product of
the force times the distance through
which the force acts.
W  Fs
Units of Work

SI
• Newton • meter = Joule



N•m=J
J = kg • m2 / s2
US Customary
• foot • pound

ft • lb
• no special name
Work, cont.
In general
W  ( F cos ) s
• F is the magnitude of the force
• s (or d) is the distance of the object moved
•  is the angle between force and direction of
motion
Work, cont.

This gives no information about
• the time it took for the motion to occur
• the velocity or acceleration of the object

Work is a scalar quantity
More About Work

The work done by a force is zero when the
force is perpendicular to the displacement
• F=0
• s=0
• cos 90° = 0

If there are multiple forces acting on an
object, the total work done is the algebraic
sum of the amount of work done by each
force
More About Work, cont.

Work can be positive or negative
• Positive if s is in the same direction as F
• Negative if s is in opposite direction to F
• Zero if s is perpendicular to F
Work Can Be Positive or
Negative


Work is positive
when lifting the
box
Work would be
negative if
lowering the box
• The force would
still be upward,
but the
displacement
would be
downward
Example
50N force pulls a 20 kg object and
moves it 2m, friction f=15N.
Acceleration along the ground? Work
done? Work done by friction? Total
work?
What about pulling at 30?
Power

Power is defined as this rate of work
•

W
P
t
SI units are Watts (W)
•
J kg  m 2
W 
3
s
s
Power, cont.

US Customary units are generally hp
• Need a conversion factor
ft lb
1 hp  550
 746 W
s
• Can define units of work or energy in terms of
units of power:


kilowatt hours (kWh) are often used in electric bills
1kWh=3.6x10^6 J
This is a unit of energy, not power
Example
A crane lifts a 5000 kg object 800 m in
10 min. How much power must the
engine produce?
Example
An 80hp outboard motor, operating at
full speed, can drive at speed boat at
11 m/s. What is the forward
thrust(force) of the motor?
W Fs
P 
 Fv
t
t
Conservation Laws



Mass
Electric Charge
Conservation of Energy
Sum of all forms of energy is conserved
Energy: ability to do work
Forms of Energy

Mechanical
• Focus for now
• May be kinetic (associated with motion)
or potential (associated with position)



Chemical
Electromagnetic
Nuclear
Some Energy Considerations

Energy can be transformed from one
form to another
• Essential to the study of physics,
chemistry, biology, geology, astronomy


From one body to another – Work!
Can be used in place of Newton’s
laws to solve certain problems more
simply
Potential Energy

Potential energy is associated with
the shape or position of the object
• Potential energy is a property of the
system, not the object
• A system is a collection of objects
interacting via forces or processes that
are internal to the system
Gravitational Potential Energy

Lift object vertically, work is done
against the force of gravity of Earth
and energy is stored in the object in
the form of Gravitational Potential
Energy (Ep)
• PE of water in reservoir is used to
generate electricity
E p  mgh
Reference Levels for Gravitational
Potential Energy

A location where the gravitational
potential energy is zero must be chosen
for each problem
• The choice is arbitrary since the change in
the potential energy is the important
quantity
• Choose a convenient location for the zero
reference height


often the Earth’s surface
may be some other point suggested by the
problem
• Once the position is chosen, it must remain
fixed for the entire problem
Example
A 1500kg pile driver lifted 20 m in the
air have EP …
Kinetic Energy




Energy associated with the motion of
an object
1 2
Ek  mv
2
Scalar quantity with the same units
as work
Work is related to kinetic energy
Work and Kinetic Energy

An object’s kinetic
energy can also be
thought of as the
amount of work
the moving object
could do in coming
to rest
• The moving
hammer has kinetic
energy and can do
work on the nail
Example
Consider energy of a falling ball of
mass m from height of h.
Energy Conservation
Energy is never created or destroyed.
Energy can be transformed from one
kind into another, but the total
amount of energy remains constant.
Example: Pendulum
Conservation of Mechanical
Energy

Conservation in general
• To say a physical quantity is conserved
is to say that the numerical value of the
quantity remains constant throughout
any physical process

In Conservation of Energy, the total
mechanical energy remains constant
E  E p  Ek  constant
Conservation of Energy, cont.

Total mechanical energy is the sum
of the kinetic and potential energies
in the system
Ei  E f
E pi  Eki  E pf  Ekf
• Other types of potential energy
functions can be added to modify this
equation
Conservation of (mechanical) Energy

True if only conservative forces are
present
• Conservative forces: gravity, springs
• Non-conservative forces: push, pull, friction,
air-resistance

Apply the conservation of energy equation
to the system
• Immediately substitute zero values, then do
the algebra before substituting the other
values

Solve for the unknown(s)
Work and Energy


If a force (other than gravity) acts on
the system and does work
Need Work-Energy relation
E pi  Eki  Wnc  E pf  Ekf

Wnc work done by non-cons. forces
1 2
1 2
mghi  mvi  W  mghf  mv f
2
2
Example
Cart on a roller-coaster with no
friction. Start from rest at h=30m.
What is the speed at the end
hA=15m.
Example
Two cars each with mass 2000kg and
speed 80km/h collide and come to
rest.
Example
Child on a 3 m high slide (no friction),
what is the speed at the end?
If a child of 25kg slides down from rest
and reaches only 3m/s. What work
was done by the frictional force
acting on the child?
If the slide is 10 m long, how large
was the average friction force?
Example
Same child is on a swing with 6m rope
and starts at 60° with respect to
vertical direction. Maximum speed?
If the child starts with speed of 1 m/s
with a push, what is the max speed?