Download Slide 1

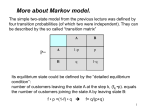
Biological Sequences and
Hidden Markov Models
CBPS7711
Sept 9, 2010
Sonia Leach, PhD
Assistant Professor
Center for Genes, Environment, and Health
National Jewish Health
[email protected]
Slides created from David Pollock’s slides from last year 7711 and current reading list from CBPS711 website
Center for Genes, Environment, and Health
Introduction
• Despite complex 3-D structure, biological molecules have
primary linear sequence (DNA, RNA, protein) or have linear
sequence of features (CpG islands, models of exons, introns,
regulatory regions, genes)
• Hidden Markov Models (HMMs) are probabilistic models for
processes which transition through a discrete set of states, each
emitting a symbol (probabilistic finite state machine)
• HMMs exhibit the ‘Markov property:’ the
conditional probability distribution of future
states of the process depends only upon the
present state (memory-less)
• Linear sequence of molecules/features is
Andrey Markov
modelled as a path through states of the HMM
1856-1922
which emit the sequence of molecules/features
• Actual state is hidden and observed only through output symbols
Center for Genes, Environment, and Health
2
Hidden Markov Model
• Finite set of N states X
• Finite set of M observations O
• Parameter set λ = (A, B, π)
– Initial state distribution πi = Pr(X1 = i)
– Transition probability aij = Pr(Xt=j | Xt-1 = i)
– Emission probability
bik = Pr(Ot=k | Xt = i)
Example:
1
2
3
N=3, M=2
π=(0.25, 0.55, 0.2)
A =  0 0.2 0.8 B =  0.1
 0 0.9 0.1


1.0 0
0 
Center for Genes, Environment, and Health
0.9 
0.75 0.25
 0.5 0.5 


3
Hidden Markov Model
• Finite set of N states X
• Finite set of M observations O
• Parameter set λ = (A, B, π)
Hidden
Markov
Model
(HMM)
X t-1 Xt
Ot-1 Ot
– Initial state distribution πi = Pr(X1 = i)
– Transition probability aij = Pr(Xt=j | Xt-1 = i)
– Emission probability
bik = Pr(Ot=k | Xt = i)
Example:
1
2
3
N=3, M=2
π=(0.25, 0.55, 0.2)
A =  0 0.2 0.8 B =  0.1
 0 0.9 0.1


1.0 0
0 
Center for Genes, Environment, and Health
0.9 
0.75 0.25
 0.5 0.5 


4
Probabilistic Graphical Models
Y X
Time
Markov Process (MP)
Xt− 1 Xt
Observability
Hidden
Markov
Model
(HMM)
X t-1 Xt
Ot-1 Ot
A t− 1
Markov
Decision
Process X t − 1
(MDP)
U t− 1
Center for Genes, Environment, and Health
At
Utility
Partially
Observable
X t Markov
Decision
Process
U (POMDP)
t
Observability
and Utility
A t− 1
Ot− 1
At
Xt− 1
Xt
U t− 1
Ut
Ot
5
Three basic problems of HMMs
1. Given the observation sequence
O=O1,O2,…,On, how do we compute
Pr(O| λ)?
2. Given the observation sequence, how do we
choose the corresponding state sequence
X=X1,X2,…,Xn which is optimal?
3. How do we adjust the model parameters to
maximize Pr(O| λ)?
Center for Genes, Environment, and Health
6
Example:
1
πi = Pr(X1 = i)
aij = Pr(Xt=j | Xt-1 = i)
bik = Pr(Ot=k | Xt = i)
2
3
N=3, M=2
π=(0.25, 0.55, 0.2)
A =  0 0.2 0.8 B =  0.1
 0 0.9 0.1


1.0 0
0 
0.9 
0.75 0.25
 0.5 0.5 


• Probability of O is sum over all state sequences
Pr(O|λ) = ∑all X Pr(O|X, λ) Pr(X|λ)
= ∑all X πx1 bx1o1 ax1x2 bx2o2 . . . axn-1xn bxnon
• Efficient dynamic programming algorithm to do
this: Forward algorithm (Baum and Welch)
Center for Genes, Environment, and Health
7
A Simple HMM
CpG Islands where in one state, much higher
probability to be C or G
0.8
G
C
A
T
.3
.3
.2
.2
CpG
0.9
0.2
0.1
G
C
A
T
.1
.1
.4
.4
Non-CpG
From David Pollock
CpG
G
C
A
T
The Forward Algorithm
0.8
.3
.3
.2
.2
0.2
G
C
A
T
Probability of a Sequence is the Sum of All Paths
that Can Produce It
G .3
0.1
.1
.1
.4
.4
0.9
G .1
Pr(G|λ) = πC bCG + πN bNG
= .5*.3 + .5*.1
For convenience, let’s drop the
0.5 for now and add it in later
G
Adapted from David Pollock’s
Non-CpG
CpG
G
C
A
T
The Forward Algorithm
0.8
.3
.3
.2
.2
0.2
G
C
A
T
Probability of a Sequence is the Sum of All Paths
that Can Produce It
G .3
0.1
.1
.1
.4
.4
0.9
(.3*.8+
.1*.1)*
.3
=.075
G .1
(.3*.2+
.1*.9)*
.1
=.015
G
C
For O=GC have 4
possible state
sequences
CC,NC,
CN,NN
Adapted from David Pollock’s
Non-CpG
CpG
G
C
A
T
The Forward Algorithm
0.8
.3
.3
.2
.2
0.2
G
C
A
T
Probability of a Sequence is the Sum of All Paths
that Can Produce It
(.3*.8+
.1*.1)
*.3
=.075
(.075*.8+
G .1
(.3*.2+
.1*.9)
*.1
=.015
(.075*.2+
.015*.9)
*.1
=.0029
G
C
G
G .3
0.1
.1
.1
.4
.4
0.9
.015*.1)
*.3
=.0185
For O=GCG
have
possible state
sequences
CCC, CCN
NCC, NCN
NNC, NNN
CNC, CNN
Adapted from David Pollock’s
Non-CpG
CpG
G
C
A
T
The Forward Algorithm
0.8
.3
.3
.2
.2
0.2
G
C
A
T
Probability of a Sequence is the Sum of All Paths
that Can Produce It
(.3*.8+
.1*.1)
*.3
=.075
(.075*.8+
G .1
(.3*.2+
.1*.9)
*.1
=.015
(.075*.2+
.015*.9)
*.1
=.0029
G
C
G
G .3
0.1
.1
.1
.4
.4
0.9
.015*.1)
*.3
=.0185
For O=GCG
have
possible state
sequences
CCC, CCN
NCC, NCN
NNC, NNN
CNC, CNN
Adapted from David Pollock’s
Non-CpG
CpG
G
C
A
T
The Forward Algorithm
0.8
.3
.3
.2
.2
0.2
G
C
A
T
Probability of a Sequence is the Sum of All Paths
that Can Produce It
G .3
0.1
.1
.1
.4
.4
0.9
G .1
G
(.3*.8+
.1*.1)
*.3
=.075
(.075*.8+
(.0185*.8
(.003*.8+
+.0029*.1
.0025*.1)
*.3
=.0185
)*.2
=.003
*.2
=.0005
(.3*.2+
.1*.9)
*.1
=.015
(.075*.2+
.015*.9)
*.1
=.0029
(.0185*.2
*.4
=.0025
(.003*.2+|
.0025*.9)
*.4
=.0011
C
G
A
A
.015*.1)
+.0029*.9)
Adapted from David Pollock’s
Non-CpG
CpG
G
C
A
T
The Forward Algorithm
0.8
.3
.3
.2
.2
0.2
G
C
A
T
Probability of a Sequence is the Sum of All Paths
that Can Produce It
G .3
0.1
.1
.1
.4
.4
0.9
Non-CpG
G .1
(.3*.8+
.1*.1)
*.3
=.075
(.075*.8+
(.3*.2+
.1*.9)
*.1
=.015
(.0185*.8
(.003*.8+
+.0029*.1
.0025*.1)
*.3
=.0185
)*.2
=.003
*.2
=.0005
(.075*.2+
.015*.9)
*.1
=.0029
(.0185*.2
(.003*.2+|
.0025*.9)
*.4
=.0011
.015*.1)
+.0029*.9)
*.4
=.0025
G
C
G
A
A
Problem 1: Pr(O| λ)=0.5*.0005 + 0.5*.0011= 8e-4
CpG
G
C
A
T
The Forward Algorithm
0.8
.3
.3
.2
.2
0.2
G
C
A
T
Probability of a Sequence is the Sum of All Paths
that Can Produce It
G .3
0.1
.1
.1
.4
.4
0.9
Non-CpG
G .1
(.3*.8+
.1*.1)
*.3
=.075
(.075*.8+
(.3*.2+
.1*.9)
*.1
=.015
(.0185*.8
(.003*.8+
+.0029*.1
.0025*.1)
*.3
=.0185
)*.2
=.003
*.2
=.0005
(.075*.2+
.015*.9)
*.1
=.0029
(.0185*.2
(.003*.2+|
.0025*.9)
*.4
=.0011
.015*.1)
+.0029*.9)
*.4
=.0025
G
C
G
A
A
Problem 2: What is optimal state sequence?
CpG
G
C
A
T
The Forward Algorithm
0.8
.3
.3
.2
.2
0.2
G
C
A
T
Probability of a Sequence is the Sum of All Paths
that Can Produce It
G .3
0.1
.1
.1
.4
.4
0.9
G .1
G
(.3*.8+
.1*.1)
*.3
=.075
(.075*.8+
(.0185*.8
(.003*.8+
+.0029*.1
.0025*.1)
*.3
=.0185
)*.2
=.003
*.2
=.0005
(.3*.2+
.1*.9)
*.1
=.015
(.075*.2+
.015*.9)
*.1
=.0029
(.0185*.2
*.4
=.0025
(.003*.2+|
.0025*.9)
*.4
=.0011
C
G
A
A
.015*.1)
+.0029*.9)
Adapted from David Pollock’s
Non-CpG
CpG
G
C
A
T
0.8
.3
.3
.2
.2
0.2
G
C
A
T
The Viterbi Algorithm
Most Likely Path (use max instead of sum)
G .3
max(
.3*.8,
.1*.1)
*.3
= .072
max(
.072*.8,
.009*.1)
*.3
= .0173
max(
.0173*.8,
.0014*.1)
*.2
=.0028
max(
.0028*.8,
.0014*.1)
*.2
=.00044
G .1
max(
.3*.2,
.1*.9)
*.1
=.009
max(
.072*.2,
.009*.9)
*.1
=.0014
max(
.0173*.2+.
0014*.9)
*.4
=.0014
max(
.0028*.2,
.0014*.9
)*.4
=.0005
G
C
G
0.1
.1
.1
.4
.4
0.9
Non-CpG
A
A
Adapted from David Pollock’s
(note error in formulas on his)
CpG
G
C
A
T
0.8
.3
.3
.2
.2
0.2
G
C
A
T
The Viterbi Algorithm
Most Likely Path: Backtracking
G .3
0.1
.1
.1
.4
.4
0.9
G .1
G
max(
max(
.3*.8,
.072*.8,
.1*.1)
*.3
= .072
.009*.1)
*.3
= .0173
max(
.3*.2,
.1*.9)
*.1
=.009
max(
.072*.2,
.009*.9)
*.1
=.0014
C
G
max(
.0173*.8,
.0014*.1)
*.2
=.0028
max(
.0028*.8,
.0014*.1)
*.2
=.00044
max(
max(
.0028*.2,
.0014*.9
)*.4
=.0005
.0173*.2
+.0014*.9)
*.4
=.0014
A
A
Adapted from David Pollock’s
Non-CpG
CpG
G
C
A
T
0.8
.3
.3
.2
.2
0.2
G
C
A
T
Forward-backward algorithm
G .3
0.1
.1
.1
.4
.4
0.9
Non-CpG
G .1
(.3*.8+
.1*.1)
*.3
=.075
(.075*.8+
(.3*.2+
.1*.9)
*.1
=.015
(.0185*.8
(.003*.8+
+.0029*.1
.0025*.1)
*.3
=.0185
)*.2
=.003
*.2
=.0005
(.075*.2+
.015*.9)
*.1
=.0029
(.0185*.2
(.003*.2+|
.0025*.9)
*.4
=.0011
.015*.1)
+.0029*.9)
*.4
=.0025
Problem
3: How
G
C to learnGmodel? A
A
Forward algorithm calculated Pr(O1..t,Xt=i| λ)
Parameter estimation by Baum-Welch
Forward Backward Algorithm
Forward variable αt(i) =Pr(O1..t,Xt=i | λ)
Backward variable βt(i) =Pr(Ot+1..N|Xt=i, λ)
Rabiner 1989
Homology HMM
• Gene recognition, classify to identify distant homologs
• Common Ancestral Sequence
–
–
–
–
–
Parameter set λ = (A, B, π), strict left-right model
Specially defined set of states: start, stop, match, insert, delete
For initial state distribution π, use ‘start’ state
For transition matrix A use global transition probabilities
For emission matrix B
• Match, site-specific emission
probabilities
• Insert (relative to ancestor), global
emission probs
• Delete, emit nothing
• Multiple Sequence Alignments
Adapted from David Pollock’s
Homology HMM
insert
start
insert
insert
match
delete
match
delete
end
Adapted from David Pollock’s
Homology HMM Example
A
C
D
E
F
.1
.05
.2
.08
.01
match
A
C
D
E
F
.04
.1
.01
.2
.02
match
A
C
D
E
F
.2
.01
.05 match
.1
.06
Ungapped blocks
Ungapped blocks
where insertion states
model intervening
sequence between
blocks
Insert/delete states
allowed anywhere
Allow multiple domains,
sequence fragments
Eddy, 1998
Center for Genes, Environment, and Health
24
Homology HMM
• Uses
– Find homologs to profile HMM in database
• Score sequences for match to HMM
– Not always Pr(O| λ) since some areas may highly diverge
– Sometimes use ‘highest scoring subsequence’
• Goal is to find homologs in database
– Classify sequence using library
of profile HMMs
• Compare alternative models
– Alignment of additional sequences
– Structural alignment when alphabet is secondary
structure symbols so can do fold-recognition, etc
Adapted from David Pollock’s
Why Hidden Markov Models for MSA?
• Multiple sequence alignment as consensus
– May have substitutions, not all AA are equal
FOS_RAT
FOS_MOUSE
IPTVTAISTSPDLQWLVQPTLVSSVAPSQTRAPHPYGLPTPSTGAYARAGVV 112
IPTVTAISTSPDLQWLVQPTLVSSVAPSQTRAPHPYGLPTQSAGAYARAGMV 112
– Could use regular expressions but how to handle indels?
FOS_RAT
FOS_MOUSE
FOS_CHICK
IPTVTAISTSPDLQWLVQPTLVSSVAPSQTRAPHPYGLPTPS-TGAYARAGVV 112
IPTVTAISTSPDLQWLVQPTLVSSVAPSQTRAPHPYGLPTQS-AGAYARAGMV 112
VPTVTAISTSPDLQWLVQPTLISSVAPSQNRG-HPYGVPAPAPPAAYSRPAVL 112
– What about variable-length members of family?
FOS_RAT
FOS_MOUSE
FOS_CHICK
FOSB_MOUSE
FOSB_HUMAN
IPTVTAISTSPDLQWLVQPTLVSSVAPSQ-------TRAPHPYGLPTPS-TGAYARAGVV
IPTVTAISTSPDLQWLVQPTLVSSVAPSQ-------TRAPHPYGLPTQS-AGAYARAGMV
VPTVTAISTSPDLQWLVQPTLISSVAPSQ-------NRG-HPYGVPAPAPPAAYSRPAVL
VPTVTAITTSQDLQWLVQPTLISSMAQSQGQPLASQPPAVDPYDMPGTS----YSTPGLS
VPTVTAITTSQDLQWLVQPTLISSMAQSQGQPLASQPPVVDPYDMPGTS----YSTPGMS
Center for Genes, Environment, and Health
112
112
112
110
110
26
Why Hidden Markov Models?
• Rather than consensus sequence which describes the
most common amino acid per position, HMMs allow
more than one amino acid to appear at each position
• Rather than profiles as position specific scoring matrices
(PSSM) which assign a probability to each amino acid in
each position of the domain and slide fixed-length
profile along a longer sequence to calculate score,
HMMs model probability of variable length sequences
• Rather than regular expressions which can capture
variable length sequences yet specify a limited subset
of amino acids per position, HMMs quantify difference
among using different amino acids at each position
Center for Genes, Environment, and Health
27

Model Comparison
• Based on
P(D | , M)
– For ML, take Pmax (D | , M)
• Usually
ln Pmax (D | , M)
– For heuristics, “score” is
– For Bayesian, calculate



to avoid numeric error
log 2 P(D |  fixed , M)
P(D | , M) * P   * P M 
Pmax (, M | D) 
  P(D | , M) * P   * P M 
– Uses ‘prior’ information on parameters
P ( )
Adapted from David Pollock’s
Parameters, 
• Types of parameters
–
–
–
–
–
–
Amino acid distributions for positions (match states)
Global AA distributions for insert states
Order of match states
Transition probabilities
Phylogenetic tree topology and branch lengths
Hidden states (integrate or augment)

• Wander parameter space (search)
– Maximize, or move according to posterior
probability (Bayes)
Adapted from David Pollock’s
Expectation Maximization (EM)
• Classic algorithm to fit probabilistic model
parameters with unobservable states
• Two Stages
– Maximize
• If know hidden variables (states), maximize model
parameters with respect to that knowledge
– Expectation
• If know model parameters, find expected values of the
hidden variables (states)
• Works well even with e.g., Bayesian to find
near-equilibrium space
Adapted from David Pollock’s
Homology HMM EM
• Start with heuristic MSA (e.g., ClustalW)
• Maximize
– Match states are residues aligned in most
sequences
– Amino acid frequencies observed in columns
• Expectation
– Realign all the sequences given model
• Repeat until convergence
• Problems: Local, not global optimization
– Use procedures to check how it worked
Adapted from David Pollock’s
Model Comparison
• Determining significance depends on
comparing two models (family vs non-family)
– Usually null model, H0, and test model, H1
– Models are nested if H0 is a subset of H1
– If not nested
• Akaike Information Criterion (AIC) [similar to empirical
Bayes] or
• Bayes Factor (BF) [but be careful]
• Generating a null distribution of statistic
– Z-factor, bootstrapping,   , parametric
bootstrapping, posterior predictive
2
Adapted from David Pollock’s
Z Test Method
• Database of known negative controls
– E.g., non-homologous (NH) sequences
~ N(, )
– Assume NH scores
• i.e., you are modeling known NH sequence scores as a normal
distribution
– Set appropriate significance level for multiple
comparisons (more
 below)
• Problems
– Is homology certain?
– Is it the appropriate null model?
• Normal distribution often not a good approximation
– Parameter control hard: e.g., length distribution
Adapted from David Pollock’s
Bootstrapping and Parametric
Models
• Random sequence sampled from the same set
of emission probability distributions
– Same length is easy
– Bootstrapping is re-sampling columns
– Parametric uses estimated frequencies, may
include variance, tree, etc.
• More flexible, can have more complex null
• Pseudocounts of global frequencies if data limit
• Insertions relatively hard to model
– What frequencies for insert states? Global?
Adapted from David Pollock’s
Homology HMM Resources
• UCSC (Haussler)
– SAM: align, secondary structure predictions, HMM
parameters, etc.
• WUSTL/Janelia (Eddy)
– Pfam: database of pre-computed HMM alignments
for various proteins
– HMMer: program for building HMMs
Adapted from David Pollock’s
Center for Genes, Environment, and Health
36
Why Hidden Markov Models?
• Multiple sequence alignment as consensus
– May have substitutions, not all AA are equal
FOS_RAT
FOS_MOUSE
IPTVTAISTSPDLQWLVQPTLVSSVAPSQTRAPHPYGLPTPSTGAYARAGVV 112
IPTVTAISTSPDLQWLVQPTLVSSVAPSQTRAPHPYGLPTQSAGAYARAGMV 112
– Could use regular expressions but how to handle indels?
FOS_RAT
FOS_MOUSE
FOS_CHICK
IPTVTAISTSPDLQWLVQPTLVSSVAPSQTRAPHPYGLPTPS-TGAYARAGVV 112
IPTVTAISTSPDLQWLVQPTLVSSVAPSQTRAPHPYGLPTQS-AGAYARAGMV 112
VPTVTAISTSPDLQWLVQPTLISSVAPSQNRG-HPYGVPAPAPPAAYSRPAVL 112
– What about variable-length members of family?
FOS_RAT
FOS_MOUSE
FOS_CHICK
FOSB_MOUSE
FOSB_HUMAN
IPTVTAISTSPDLQWLVQPTLVSSVAPSQ-------TRAPHPYGLPTPS-TGAYARAGVV
IPTVTAISTSPDLQWLVQPTLVSSVAPSQ-------TRAPHPYGLPTQS-AGAYARAGMV
VPTVTAISTSPDLQWLVQPTLISSVAPSQ-------NRG-HPYGVPAPAPPAAYSRPAVL
VPTVTAITTSQDLQWLVQPTLISSMAQSQGQPLASQPPAVDPYDMPGTS----YSTPGLS
VPTVTAITTSQDLQWLVQPTLISSMAQSQGQPLASQPPVVDPYDMPGTS----YSTPGMS
112
112
112
110
110
– (but don’t accept everything – typically introduce gap penalty)
Center for Genes, Environment, and Health
37
Why Hidden Markov Models?
• Rather than consensus sequence which describes the
most common amino acid per position, HMMs allow
more than one amino acid to appear at each position
• Rather than profiles as position specific scoring matrices
(PSSM) which assign a probability to each amino acid in
each position of the domain and slide fixed-length
profile along a longer sequence to calculate score,
HMMs model probability of variable length sequences
• Rather than regular expressions which can capture
variable length sequences yet specify a limited subset
of amino acids per position, HMMs quantify difference
among using different amino acids at each position
Center for Genes, Environment, and Health
38
Acknowledgements
Center for Genes, Environment, and Health
39