* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download PPT
Investment management wikipedia , lookup
Pensions crisis wikipedia , lookup
Greeks (finance) wikipedia , lookup
Credit card interest wikipedia , lookup
Land banking wikipedia , lookup
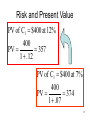
Rate of return wikipedia , lookup
Financial economics wikipedia , lookup
Investment fund wikipedia , lookup
Financialization wikipedia , lookup
Interest rate wikipedia , lookup
Mark-to-market accounting wikipedia , lookup
Stock valuation wikipedia , lookup
Stock selection criterion wikipedia , lookup
Modified Dietz method wikipedia , lookup
Continuous-repayment mortgage wikipedia , lookup
Global saving glut wikipedia , lookup
Internal rate of return wikipedia , lookup
Business valuation wikipedia , lookup
Time value of money wikipedia , lookup
Supplementary Notes • • • • Present Value Net Present Value NPV Rule Opportunity Cost of Capital 1 Present Value Present Value Discount Factor Value today of a future cash flow. Present value of a $1 future payment. Discount Rate Interest rate used to compute present values of future cash flows. 2 Present Value Present Value = PV PV = discount factor C1 3 Present Value Discount Factor = DF = PV of $1 DF 1 (1 r ) t Discount Factors can be used to compute the present value of any cash flow. 4 Valuing an Office Building Step 1: Forecast cash flows Cost of building = C0 = 350 Sale price in Year 1 = C1 = 400 Step 2: Estimate opportunity cost of capital If equally risky investments in the capital market offer a return of 7%, then Cost of capital = r = 7% 5 Valuing an Office Building Step 3: Discount future cash flows PV C1 (1r ) 400 (1.07) 374 Step 4: Go ahead if PV of payoff exceeds investment NPV 350 374 24 6 Net Present Value NPV = PV - required investment C1 NPV = C0 1 r 7 Risk and Present Value • Higher risk projects require a higher rate of return. • Higher required rates of return cause lower PVs. PV of C1 $400 at 7% 400 PV 374 1 .07 8 Risk and Present Value PV of C1 $400 at 12% 400 PV 357 1 .12 PV of C1 $400 at 7% 400 PV 374 1 .07 9 Net Present Value Rule • Accept investments that have positive net present value. Example Suppose we can invest $50 today and receive $60 in one year. Should we accept the project given a 10% expected return? 60 NPV = -50 + $4.55 1.10 10 Opportunity Cost of Capital Example You may invest $100,000 today. Depending on the state of the economy, you may get one of three possible cash payoffs: Economy Payoff Slump Normal Boom $80,000 110,000 140,000 80,000 110,000 140,000 Expected payoff C1 $110,000 3 11 Opportunity Cost of Capital Example - continued The stock is trading for $95.65. Depending on the state of the economy, the value of the stock at the end of the year is one of three possibilities: Economy Slump Stock Pric e $80 Normal 110 Boom 140 12 Opportunity Cost of Capital Example - continued The stocks expected payoff leads to an expected return. 80 100 140 Expected payoff C1 $110 3 expected profit 110 95.65 Expected return .15 or 15% investment 95.65 13 Opportunity Cost of Capital Example - continued Discounting the expected payoff at the expected return leads to the PV of the project. 110,000 PV $95,650 1.15 14 Investment vs. Consumption • Some people prefer to consume now. Some prefer to invest now and consume later. • Borrowing and lending allows us to reconcile these opposing desires which may exist within the firm’s shareholders. 15 Investment vs. Consumption income in period 1 100 An 80 Some investors will prefer A and others B 60 40 Bn 20 20 40 60 income in period 0 80 100 16 Investment vs. Consumption The grasshopper (G) wants to consume now. The ant (A) wants to wait. But each is happy to invest. A prefers to invest 14%, moving up the red arrow, rather than at the 7% interest rate. G invests and then borrows at 7%, thereby transforming $100 into $106.54 of immediate consumption. Because of the investment, G has $114 next year to pay off the loan. The investment’s NPV is $106.54-100 = 17 +6.54 Investment vs. Consumption • Dollars Later A invests $100 now and consumes $114 next year 114 107 The grasshopper (G) wants to consume now. The ant (A) wants to wait. But each is happy to invest. A prefers to invest 14%, moving up the red arrow, rather than at the 7% interest rate. G invests and then borrows at 7%, thereby transforming $100 into $106.54 of immediate consumption. Because of the investment, G has $114 next year to pay off the loan. The investment’s NPV is $106.54-100 = +6.54 G invests $100 now, borrows $106.54 and consumes now. 100 106.54 Dollars Now 18 Topics Covered • • • • • Valuing Long-Lived Assets PV Calculation Short Cuts Compound Interest Interest Rates and Inflation Example: Present Values and Bonds 19 Present Values Discount Factor = DF = PV of $1 DF 1 t (1 r ) • Discount Factors can be used to compute the present value of any cash flow. 20 Present Values C1 PV DF C1 1 r1 DF 1 (1 r ) t • Discount Factors can be used to compute the present value of any cash flow. 21 Present Values Ct PV DF Ct 1 rt • Replacing “1” with “t” allows the formula to be used for cash flows that exist at any point in time. 22 Present Values Example You just bought a new computer for $3,000. The payment terms are 2 years same as cash. If you can earn 8% on your money, how much money should you set aside today in order to make the payment when due in two years? PV 3000 (1.08) 2 $2,572.02 23 Present Values • PVs can be added together to evaluate multiple-periods cash flows. PV C1 (1 r ) (1r ) 2 .... C2 1 24 Present Values • Given two dollars, one received a year from now and the other two years from now, the value of each is commonly called the Discount Factor. Assume r1 = 20% and r2 = 7%. 25 Present Values • Given two dollars, one received a year from now and the other two years from now, the value of each is commonly called the Discount Factor. Assume r1 = 20% and r2 = 7%. DF1 1.00 (1.20)1 .83 DF2 1.00 (1.07 ) 2 .87 26 Present Values Example Assume that the cash flows from the construction and sale of an office building is as follows. Given a 7% required rate of return, create a present value worksheet and show the net present value. Year 0 Year 1 Year 2 150,000 100,000 300,000 27 Present Values Example - continued Assume that the cash flows from the construction and sale of an office building is as follows. Given a 7% required rate of return, create a present value worksheet and show the net present value. Period 0 1 2 Discount Factor 1.0 1 1.07 .935 1 .873 1.07 2 Cash Present Flow Value 150,000 150,000 100,000 93,500 300,000 261,900 NPV Total $18,400 28 Short Cuts • Sometimes there are shortcuts that make it very easy to calculate the present value of an asset that pays off in different periods. These tolls allow us to cut through the calculations quickly. 29 Short Cuts Perpetuity - Financial concept in which a cash flow is theoretically received forever. cash flow Return present va lue C r PV 30 Short Cuts Perpetuity - Financial concept in which a cash flow is theoretically received forever. cash flow PV of Cash Flow discount rate C1 PV r 31 Short Cuts Annuity - An asset that pays a fixed sum each year for a specified number of years. 1 1 PV of annuity C t r r 1 r 32 Annuity Short Cut Example You agree to lease a car for 4 years at $300 per month. You are not required to pay any money up front or at the end of your agreement. If your opportunity cost of capital is 0.5% per month, what is the cost of the lease? 33 Annuity Short Cut Example - continued You agree to lease a car for 4 years at $300 per month. You are not required to pay any money up front or at the end of your agreement. If your opportunity cost of capital is 0.5% per month, what is the cost of the lease? 1 1 Lease Cost 300 48 .005 .0051 .005 Cost $12,774.10 34 Compound Interest i ii Periods Interest per per year period iii APR (i x ii) iv Value after one year v Annually compounded interest rate 1 6% 6% 1.06 6.000% 2 3 6 1.032 = 1.0609 6.090 4 1.5 6 1.0154 = 1.06136 6.136 12 .5 6 1.00512 = 1.06168 6.168 52 .1154 6 1.00115452 = 1.06180 6.180 365 .0164 6 1.000164365 = 1.06183 6.183 35 18 16 14 12 10 8 6 4 2 0 10% Simple 30 27 24 21 18 15 12 9 6 10% Compound 3 0 FV of $1 Compound Interest Number of Years 36