Download chapter1

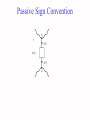
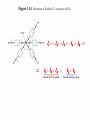
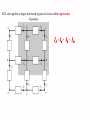
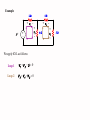
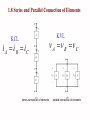
1.2 Voltage
Voltage is the energy per unit charge created by the separation,
which can be expressed as
v  dw
dq
Volt (joule/coulumb)
where
v = the voltage in volts
w = the energy in joules
q = the charge in coulombs
1.3 The Current
The rate of flow of charges is called the current which is expressed as
i  dq
dt
Ampere (coulumb/second)
where
i = the current in amperes
q = the charge in coulombs
t = the time in seconds
Power
Power is defined as the time rate of expanding or absorbing
energy
P  dw
dt
where
1 W1 J
1s
W
P  power in Wattts
w  Energy in Joules
t  Time in Seconds
 dw
dw
P
= 
dt
 dq




 dq

 dt





vi
This shows that the power is simply the product of the current in the element and the
voltage across the element
Passive Sign Convention
Figure 1.10
Charging a
discharged
automobile
battery to
illustrate the
concept of
power delivered
to or absorbed
by an element
and the passive
sign convention.
Figure 1.11
Illustration of the power delivered to (absorbed by) an element and the
power delivered by the element.
Figure 1.12
Examples of the computation of power delivered to or by an element.
Electric Circuit
Figure 1.13
Illustration of an electric circuit as a particular interconnection of circuit elements.
Kirchhoff's Current Law ( KCL):
The algebraic sum of all the currents at any node in a circuit equals zero.
i1
i2
i3
Current entering the node is positive and leaving the node is negative
i1  (  i 2 )  i 3
0
 i1  i 2

i3
0
Current entering the node is negative and leaving the node is positive
(i1 ) 
i2
 (i 3 )  0
 i1  i 2

i3
0
Note the algebraic sign is regardless if the sign on the value of the current
Figure 1.14
Illustration of Kirchhoff ’s current law (KCL).
i1  (  i 2 )  i 3  (  i 4 )  i 5

i1  i 3  i 5
currents Entering a node

i2  i4
currents Leaving a node
0
KCL also applies to larger and closed regions of circuit called supernodes
i 2  i 6  i 9  i10
Example 1.3: Determine the currents ix, iy and iz
KCL at node d
ix+3=2
ix = 2-3 = -1A
KCL at node a
ix+ iy +4 = 0
iy = -3A
KCL at node b
4 + iz + 2 = 0
iz = -6A
We could have applied KCL at the supernode to get
iy + 4A + 2A = 3A
Thus iy = -3
Figure 1.17
Example 1.4.
Kirchhoff Voltage Law (KVL)
The algebraic sum of all the voltages around any closed path in a circuit equals zero.
First we have to define a closed path
a
b
c
+

f
e
d
A closed path or a loop is defined as starting at an arbitrary node, we trace closed path in
a circuit through selected basic circuit elements including open circuit and return to the
original node without passing through any intermediate node more than once
abea
bceb
cdec
aefa
abcdefa
Kirchhoff Voltage Law (KVL)
The algebraic sum of all the voltages around any closed path in a circuit equals zero.
2W
+
3W
v1 
+
+
5V
+

v2

6W
v3 
+
v4
5W

The "algebraic" correspond to the reference direction to each voltage in the loop.
Assigning a positive sign to a voltage rise (  to + )
Assigning a negative sign to a voltage drop (  to  )
OR
Assigning a positive sign to a voltage drop (  to  )
Assigning a negative sign to a voltage rise (  to  )
Example
2W
+
3W
v1 
+
+
5V
v2
+


We apply KVL as follows:
Loop 1
v1 v 2  5
0
Loop 2
v 3 v 4 v 2
0
6W
v3 
+
v4

5W
Figure 1.23
Another example of the application of KVL.
Ex 1.8:
Determine vx, vy, vz by KVL
vz  2  5  (4)  7
v y  3  6  5  8
vx  6  2  vz  4  11  15
Ex 1.9: Determine voltage v and current i
KVL around loop E,H,B,A,G gives
v  3  2 1  4  4
KCL at the supernode gives 1+4+ix=3, thus ix =-2A
KCL at node e gives i+3=-2, thus i=-5A
1.7 Conservation of Power
The sum of powers delivered to all elements of a circuit
at any time equals to zero

allelements
pi 

allelements
vi ii  0
Ex 1.10 Verify conservation of power for the circuit
ic = -3A, vc = 3V
id = -5A, vd = 1V
ve = v = -4V
Element
power
A
1A x 1V=1W
B
-4A x 2V=-8W
C
-3A x 3V=-9W
D
-5A x 1V=-5W
E
-3A x (-4V)=12W
F
5A x (-1V)=-5W
G
2A x 4V=8W
H
-(-2A) x 3V=6W
if = 5A, vf = -1V
ih = ix = -2A
1.8 Series and Parallel Connection of Elements
v A  vKVL
B v C
 vv
v Cv C
BB
i vvAA i
i
Figure 1.32
KCL
i A  i B  iC
A
series connection of elements,
B
C
parallel connection of elements
Figure 1.33
Example to illustrate to proper classification of series and
parallel connections
Determine which elements are connected in series
and which elements are connected in parallel
Figure E1.19
Exercise Problem 1.19.
Determine which elements are connected in series
and which elements are connected in parallel
Figure E1.20
Exercise Problem 1.20.
HW 1 is due now