* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download View File
Linear time-invariant theory wikipedia , lookup
Control system wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Buck converter wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Power inverter wikipedia , lookup
Two-port network wikipedia , lookup
Flip-flop (electronics) wikipedia , lookup
Power electronics wikipedia , lookup
Power MOSFET wikipedia , lookup
Schmitt trigger wikipedia , lookup
Solar micro-inverter wikipedia , lookup
Immunity-aware programming wikipedia , lookup
Integrated circuit wikipedia , lookup
Network analysis (electrical circuits) wikipedia , lookup
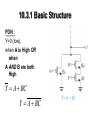
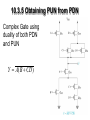
EE210 Digital Electronics Class Lecture 9 April 08, 2009 In This Class Digital CMOS Logic Circuits We Will Discuss: 10.3 CMOS Logic-Gate Circuits 2 Chapter 10: Digital CMOS Logic Circuits We will Start from 10.3 CMOS Logic-Gate Circuits But First Home Work# 03… Home Work# 03… For the circuit in Fig., consider the application of inputs of 5 V and 0.2 V to X and Y in any combination ,and find the output voltage for each combination . • Tabulate your results. How many input combinations are there? (4 Marks) •What happens when any input is high? (3 Marks) • What happens when both inputs are low? (3 Marks) 10.3 CMOS Logic-Gate Circuits • Using Inverter knowledge we consider CMOS ckts that realize combinationallogic functions • In combinational ckts output at any time is function only of the value of input signal at that time. Thus, these do not have memory. • Combinational-logic circuits are used in large quantities in many applications. Indeed, every digital system contains large numbers of Combinational-logic circuits 10.3.1 Basic Structure • CMOS logic ckt is extension or generalization of the CMOS Inverter • As we learned, CMOS inverter consists of NMOS pull-down transistor, and a PMOS pull-up transistor, operated by input voltage in complementary fashion 10.3.1 Basic Structure • CMOS Logic Gate has two Networks: Pull-Down Network (PDN) constructed of NMOS transistors and Pull-up Network (PUN) constructed of PMOS Transistors • Two Networks are Operated by Input Variables, in Complementary fashion 10.3.1 Basic Structure • When All Three input combinations are High PDN will conduct and will Pull the output node down to Ground making Output Low (Y=0) (Voltage Zero) • Simultaneously, PUN will be OFF and no path will Exists between VDD and Ground 10.3.1 Basic Structure • When All Three input combinations are Low PUN will conduct and will Pull the output node Up to VDD making Output High (Y=1) (Voltage = VDD ) • Simultaneously, PDN will be OFF and no path will Exists between VDD and Ground 10.3.1 Basic Structure • PDN and PUN each Utilize Devices in Parallel to form an OR Function PDN : QA will conduct when A is Hi and will Pull the Output Down to ground (Y=0) QB will conduct when B is Hi and will Pull the Output Down to ground (Y=0) Thus Y=0, when A OR B is High Y A B Y A B 10.3.1 Basic Structure • PDN and PUN each Utilize Devices in Parallel to form an OR Function PUN : QA will conduct when A is Lo and will Pull the Output Up to VDD (Y=1) QB will conduct when B is Lo and will Pull the Output Up to VDD (Y=1). Thus Y=1 (Hi), when A OR B is Lo Y A B 10.3.1 Basic Structure • PDN and PUN each Utilize Devices in Series to form an AND Function PDN : QA and QB will conduct ONLY when both A and B are Hi Simultaneously. Thus Y=0 (low), when A is High AND B is High Y AB Y AB 10.3.1 Basic Structure • PDN and PUN each Utilize Devices in Series to form an AND Function PUN : QA and QB will conduct ONLY when both A and B are Lo Simultaneously. Thus Y=1 (High), when A is High AND B is High Y AB 10.3.1 Basic Structure PDN : Y=0 (low), when A is High OR when A AND B are both High Y A BC Y A BC 10.3.1 Basic Structure PUN : Y=1 (low), when A is Lo OR when A AND B are both Lo Y A BC 10.3.1 Basic Structure • After understanding structure and operation of PDNs and PUNs we will consider complete CMOS gates • BUT Before that we need to introduce alternative ckt symbols which are almost universally used for MOS transistors by digital-ckt designers 10.3.1 Basic Structure • Circle at Gate Terminal for PMOS indicate that the Signal at gate has to be low for it to be activated (conduct) • These symbol omit indication of source and drain Basic Boolean Identities Fundamental Laws: OR AND A0A A0 0 A 1 1 A1 A AA A AA A A A 1 AA 0 Associative Law: (A B) C A (B C) (AB)C A(BC) NOT (Inverter) A A 1 AA 0 A A Commutative Law A B B A AB BA Basic Boolean Identities Distributive Law: A(B C) AB AC DeMorgan’s Law: AB... A B ... A B ... AB... Auxiliary Identities: A AB A A AB A B ( A B)( A C ) A BC PDN : Y=0 (Low), when A OR B is High Y A B Y A B PUN : Y=1 (High), when A is Low AND B is Low Y AB 10.3.2 Two Input NOR Gate Combining both PDN and PUN realizes Complete CMOS NOR Gate with NOR Function Y A B AB Input A 0 0 1 1 B 0 1 0 1 Output Y 1 0 0 0 PDN : Y=0 (low), when A is High AND B is High Y AB Y AB PUN : Y=1 (Hi), when A OR B is Lo Y A B 10.3.3 Two Input NAND Gate Combining both PDN and PUN realizes Complete CMOS NAND Gate with NAND Function Y AB A B Input A 0 0 1 1 B 0 1 0 1 Output Y 1 1 1 0 10.3.4 A Complex Gate Consider More Complex Logic Function Y A( B CD) Y A( B CD) Y should be Low for A High AND Simultaneously either B High OR C AND D both High. The PDN for this is. To get PUN we need to Express Y in terms of Complemented variables 10.3.4 A Complex Gate So we use DeMorgan’s Law Y A( B CD) A B CD A BCD A B(C D) Thus, Y is High for A OR B Low AND either C OR D Low. Thus PUN for this is. 10.3.4 A Complex Gate Combining both PDN and PUN realizes Complete CMOS Complex Gate Function Y A( B CD) 10.3.5 Obtaining PUN from PDN • So far, we have seen that PDN and PUN are dual networks: A series branch exist in one and Parallel branch exist in other. • Thus, we can obtain one from the other – a simple process than using Boolean expressions. • For Complex Gate we found PDN relatively easy Y (bar) in terms of uncomplemented inputs. We could obtain PUN using this duality method instead of Boolean Expression. 10.3.5 Obtaining PUN from PDN 10.3.5 Obtaining PUN from PDN Complex Gate using duality of both PDN and PUN Y A( B CD) 10.3.6 Exclusive OR Function (XOR) • An important Function that is often used in logic design is the Exclusive-OR (XOR) function: Y AB AB • Y instead of Y(bar) is given so we can synthesize PUN easily. • Unfortunately Y is not function of complemented variables only, thus we will need additional inverters. 10.3.6 Exclusive OR Function (XOR) PUN Obtained directly from: Y AB AB Note that we have used two inverters to generate A(bar) and B(bar) PDN can be synthesized from PUN using duality or developing the Y(bar) expression. 10.3.6 Exclusive OR Function (XOR) First: PDN from PUN using duality Second: develop the Y(bar) expression using DeMorgan Law on Y AB AB Gives Y AB A B 10.3.6 Exclusive OR Function (XOR) So the complete XOR using PUN and PDN Y AB AB Note that we have used two inverters to generate A(bar) and B(bar) which are not shown. XOR requires 12 transistors 10.3.7 Synthesis Method Summary • To synthesize PDN we need Y(bar) expression in terms of uncomplemented variables. If complemented variables appear in expression we need inverters. • To synthesize PUN we need Y expression in terms of complemented variables and then apply uncomplemented variables to the gates of PMOS transistors. If uncomplemented variables appear in expression we need inverters. • PDN can be obtained from PUN (and vice versa) using duality In Next Class We Will Continue to Discuss: CMOS Logic Gates