* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Slides
Wireless power transfer wikipedia , lookup
Utility frequency wikipedia , lookup
Stray voltage wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Power inverter wikipedia , lookup
Buck converter wikipedia , lookup
Power over Ethernet wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Audio power wikipedia , lookup
Power factor wikipedia , lookup
Single-wire earth return wikipedia , lookup
Power electronics wikipedia , lookup
Voltage optimisation wikipedia , lookup
Electrical substation wikipedia , lookup
Electric power system wikipedia , lookup
Electrification wikipedia , lookup
Transformer wikipedia , lookup
Amtrak's 25 Hz traction power system wikipedia , lookup
Switched-mode power supply wikipedia , lookup
Mains electricity wikipedia , lookup
History of electric power transmission wikipedia , lookup
Alternating current wikipedia , lookup
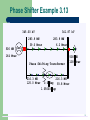
ECE 476 POWER SYSTEM ANALYSIS Lecture 10 Transformers, Generators, Load, Ybus Professor Tom Overbye Department of Electrical and Computer Engineering Announcements Be reading Chapter 6. HW 3 is due now. HW 4 is 3.4, 3.10, 3.14, 3.19, 3.23, 3.60; due September 29 in class. First exam is October 11 during class. Closed book, closed notes, one note sheet and calculators allowed 1 Load Tap Changing Transformers LTC transformers have tap ratios that can be varied to regulate bus voltages The typical range of variation is 10% from the nominal values, usually in 33 discrete steps (0.0625% per step). Because tap changing is a mechanical process, LTC transformers usually have a 30 second deadband to avoid repeated changes. Unbalanced tap positions can cause "circulating vars" 2 LTCs and Circulating Vars slack 64 MW 14 Mvar 1.00 pu 1 24.1 MW 12.8 Mvar 40.2 MW 1.7 Mvar 1.000 tap A A 80% 1.056 tap MVA MVA 40.0 MW -0.0 Mvar 24.0 MW -12.0 Mvar 0.98 pu 2 3 1.05 pu 0.0 Mvar 24 MW 12 Mvar 40 MW 0 Mvar 3 Phase Shifting Transformers Phase shifting transformers are used to control the phase angle across the transformer Since power flow through the transformer depends upon phase angle, this allows the transformer to regulate the power flow through the transformer Phase shifters can be used to prevent inadvertent "loop flow" and to prevent line overloads. 4 Phase Shifter Example 3.13 345.00 kV 500 MW 341.87 kV 283.9 MW 39.0 Mvar 283.9 MW 6.2 Mvar slack 164 Mvar Phase Shifting Transformer 216.3 MW 125.0 Mvar 500 MW 100 Mvar 216.3 MW 0.0 deg 93.8 Mvar 1.05000 tap 5 ComED Control Center 6 ComED Phase Shifter Display 7 Phase Shifting Transformer Picture Costs about $7 million, weighs about 1.2 million pounds 230 kV 800 MVA Phase Shifting Transformer During factory testing Source: Tom Ernst, Minnesota Power 8 Autotransformers Autotransformers are transformers in which the primary and secondary windings are coupled magnetically and electrically. This results in lower cost, and smaller size and weight. The key disadvantage is loss of electrical isolation between the voltage levels. Hence autotransformers are not used when a is large. For example in stepping down 7160/240 V we do not ever want 7160 on the low side! 9 Could it Happen Tomorrow? Geomagnetic disturbances (GMDs) impact the power grid by causing geomagenetic induced dc currents (GICs) that can push the transformers into saturation. Saturated transformers have high harmonics which leads to high reactive losses and heating Image from Ed Schweitzer June 2011 JASON Presentation 10 Could It Happen Tomorrow? • • A 1989 storm caused a major blackout in Quebec. Much larger storms have occurred in the past, such as in 1859, which knocked out much of the telegraph system in the Eastern US A 2010 Metatech Report indicated an 1859 type event could destroy hundreds of EHV transformers, crippling our grid for months! Metatech R-319, Figure 4.11 11 Load Models Ultimate goal is to supply loads with electricity at constant frequency and voltage Electrical characteristics of individual loads matter, but usually they can only be estimated – – actual loads are constantly changing, consisting of a large number of individual devices only limited network observability of load characteristics Aggregate models are typically used for analysis Two common models – – constant power: Si = Pi + jQi constant impedance: Si = |V|2 / Zi 12 Generator Models Engineering models depend upon application Generators are usually synchronous machines For generators we will use two different models: – – a steady-state model, treating the generator as a constant power source operating at a fixed voltage; this model will be used for power flow and economic analysis a short term model treating the generator as a constant voltage source behind a possibly time-varying reactance 13 Power Flow Analysis We now have the necessary models to start to develop the power system analysis tools The most common power system analysis tool is the power flow (also known sometimes as the load flow) – – – – power flow determines how the power flows in a network also used to determine all bus voltages and all currents because of constant power models, power flow is a nonlinear analysis technique power flow is a steady-state analysis tool 14 Linear versus Nonlinear Systems A function H is linear if H(a1m1 + a2m2) = a1H(m1) + a2H(m2) That is 1) the output is proportional to the input 2) the principle of superposition holds Linear Example: y = H(x) = c x y = c(x1+x2) = cx1 + c x2 Nonlinear Example: y = H(x) = c x2 y = c(x1+x2)2 ≠ (cx1)2 + (c x2)2 15 Linear Power System Elements Resistors, inductors, capacitors, independent voltage sources and current sources are linear circuit elements 1 V = R I V = j L I V = I j C Such systems may be analyzed by superposition 16 Nonlinear Power System Elements Constant power loads and generator injections are nonlinear and hence systems with these elements can not be analyzed by superposition Nonlinear problems can be very difficult to solve, and usually require an iterative approach 17 Nonlinear Systems May Have Multiple Solutions or No Solution Example 1: x2 - 2 = 0 has solutions x = 1.414… Example 2: x2 + 2 = 0 has no real solution f(x) = x2 - 2 two solutions where f(x) = 0 f(x) = x2 + 2 no solution f(x) = 0 18 Multiple Solution Example 3 The dc system shown below has two solutions: where the 18 watt load is a resistive load The equation we're solving is 2 9 volts I RLoad RLoad 18 watts 1 +R Load What is the One solution is R Load 2 maximum Other solution is R Load 0.5 PLoad? 2 19

























![Dynamic VAR`s [D-VAR]](http://s1.studyres.com/store/data/008161131_1-082e6e1fddaf6a197897b251ba053ae1-150x150.png)




