* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download No Slide Title
Mercury-arc valve wikipedia , lookup
Three-phase electric power wikipedia , lookup
Variable-frequency drive wikipedia , lookup
Power engineering wikipedia , lookup
Spark-gap transmitter wikipedia , lookup
History of electric power transmission wikipedia , lookup
Power inverter wikipedia , lookup
Schmitt trigger wikipedia , lookup
Pulse-width modulation wikipedia , lookup
Current source wikipedia , lookup
Resistive opto-isolator wikipedia , lookup
Electrical ballast wikipedia , lookup
Power MOSFET wikipedia , lookup
Surge protector wikipedia , lookup
Voltage regulator wikipedia , lookup
Stray voltage wikipedia , lookup
Distribution management system wikipedia , lookup
Capacitor discharge ignition wikipedia , lookup
Power electronics wikipedia , lookup
Electrical substation wikipedia , lookup
Voltage optimisation wikipedia , lookup
Opto-isolator wikipedia , lookup
RLC circuit wikipedia , lookup
Network analysis (electrical circuits) wikipedia , lookup
Alternating current wikipedia , lookup
Mains electricity wikipedia , lookup
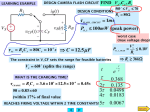
LEARNING EXAMPLE
DESIGN CAMERA FLASH CIRCUIT
FIND VS , C F , R1
DESIGN CONDITIONS
FLASH _ CIRCUIT 1ms
50V VCF 70
RB 80
PR _1 100mW (peak power)
worst case
(max voltage drop)
FC RB C F 80C F 103 s C 12.5 F
PR _1_ PEAK
R1 36k
The constraint in V_CF sets the range for feasible batteries
VS 60V (splits the range)
t
R C 3.6 10 12.5 10 0.45 s
2
3
50 0.83 60
4
(within 17% of final value
REACHES FIRING VOLTAGE WITHIN 2 TIME CONSTANTS! 5
WHAT IS THE CHARGING TIME?
4
CHARGE
1
F
6
VS2
0.1W
R1
t
e
0.368
0.135
0.0498
0.0183
0.0067
ALTERNATOR CIRCUIT TO GENERATE HIGH VOLTAGE PULSES
FROM A SMALL DC VOLTAGE SOURCE
LEARNING EXAMPLE
Single pole-double throw (SPDT) switch
Connected to battery for T1 seconds
T1
DESIGN SPEC
v PEAK 500V
100 5 T1
500 T1 1ms
3
10
VIN T1
1 T
pos 1: i ( t ) 0 VIN dt
L
L
TIME TO DISCHARCHE?
1
Current through inductor when switch
moves to pos2
pos 2: t T1 i ( t )
VIN T1
e
L
t T1
vO ( t ) Ri ( t )
L
R
v PEAK v (T1 )
RVIN T1
L
DESIGN EQUATION
DISCHARGE
103
s 10 S
100
In 5 time constants the voltage is
below 1% of initial value
Put a safety margin and wait
a bit more (1ms?)
LEARNING APPLICATION
HEART PACEMAKER
i SCR
50 A
Find R so that the SCR is ready to fire
after one second of capacitor charging
Simplified SCR model
5 v SCR
1
SCR “fires”
Charging phase
t
vC (t ) K1 K 2e , t 0
RC 106 R
vC () 6V K1
vC (0) 0.2V K1 K 2
vC (t ) 6 5.8e
As soon as the SCR switches off the
capacitor starts charging. Hence, assume
vC (0) 0.2
K1 6
K 2 5 .8
t
RC ,
t 0
Required : vC (1) 5V 6 5.8e
1
e RC
5.8
1
RC
1
1.758 R 569k
RC .569
RC
THE DISCHARGE STAGE
With the chosen resistor discharge starts
after one second and the capacitor voltage
is 5V
vC (t ) K1 K 2e
( t 1)
0.569 s
, t 1 v (1) 5V
C
vC () 6 RI 6 0.569 106 () 50 106 ( A)
K1 22.45
K1 K 2 5 K 2 27.45
vC (t ) 22.45 27.45e
( t 1)
0.569
t 1
For SCR turn off vC (1 Toff ) 0.2
Toff
e 0.569
27.45
Toff 0.11s
22.65
%example6p12
%visualizes one cycle of pacemaker
%charge cycle
tau=0.569;
tc=linspace(0,1,200);
vc=6-5.8*exp(-tc/tau);
%discharge cycle. SCR on
td=linspace(1,1.11,25);
vcd=-22.45+27.45*exp(-(td-1)/tau);
plot(tc,vc,'bd',td,vcd,'ro'),grid,
title('PACEMAKER CYCLE')
xlabel('time(s)'), ylabel('voltage(V)')
legend('SCR off', 'SCR on')
LEARNING EXAMPLE
ANALYSIS AND CONTROL OF “INDUCTIVE KICK”
DETERMINE PEAK VOLTAGES ACROSS INDUCTOR AND SWITCH.
Current in steady state is 1A before switching
di
1 t
vL (t ) L (t ) e ; t 0
dt
t
iL (t ) K 1 K 2e , t 0
K 1 K 2 iL (0 ) 1
K 2 i L ( ) 0
v L !! (inductive kick )
t
iL (t ) e , t 0
v SWITCH !( KVL must hold )
vC (0 ) vC (0 ) 0
i L (0 ) i L (0 ) 1 A
v SWITCH (0 ) 1 R[V ]
L
0 (switch open R )
R
Trying to make discontinuous the
inductor current!!!
circuit is now second order and may oscilla
1
R 1
Ch. Eq.: s 2
s
0
LC
L
v SWITCH 199V ! Select R, C for adequate damping and
natural frequency;e . g ., 1, 10
6
n
Circuit to control kick
snubber
circuit
R1 2
1
2 n
; n
L
LC
DESIGN EQS.
R 199 , C 10nF
LEARNING EXAMPLE
BOOSTER CONVERTER
e.g. booster
STANDARD DC POWER SUPPLY
BOOSTER “ON” PERIOD
Energy is stored in inductor.
Capacitor discharges
BOOSTER “OFF” PERIOD
Inductor releases energy.
Capacitor charges
Inductor current at the beginning of ON period MUST be the same than the current
at the end of OFF period
THE “ON” CYCLE
I 0 i (ton )
Io I0
Vo
t
1 on
V
i L (ton ) i (0) v L ( x )dx I 0 in ton
L0
L
ton toff
toff
Vin V0
toff
L
Vin
V V0
ton in
toff
L
L
Vin V0 Vin (hence booster)
Period :
T ton toff
Duty cycle : D
THE “OFF” CYCLE t ton
V0 Vin
ton
T
1
1 D
By adjusting the duty cycle one can
adjust the output voltage level
t
1 off
i L (ton toff ) i (ton ) v L ( x )dx
L ton
SIMPLIFYING ASSUMPTION: THE OUTPUT
VOLTAGE (Vo) IS CONSTANT
v L Vin V0
LEARNING BY DESIGN
DESIGN OF ELECTRIC HEATER USING A 24V SOURCE AND
1 OHM HEATING ELEMENT
100W P 400W
Solution one
Too much
power
lost in
rheostat
Pos 1
pos 2
Controlling switching frequency
one controls I_peak and average
power … And no power loss!
SWITCHED INDUCTOR
ALTERNATIVE
LEARNING EXAMPLE
DESIGN DECOUPLING CAPACITOR TO ISOLATE LOAD
FROM VARIATION IN SUPPLY VOLTAGE
Qualitative operation
acceptable
model for
supply variation
VS : EXPECTED SPIKE
decoupling
capacitor
t ' : EXPECTED DURATION
CIRCUIT AT t=0+
STEADY STATE AFTER SWITCHING
VO (0)
VO
DESIGN EQUATION FOR DECOUPLING CAPACITOR
LEARNING BY DESIGN FIND C SUCH THAT i (t ) IS OVERDAMPED , AND SATISFIES :
(1) Reaches 1A within 100ms;
(2) Stays above 1A between 1s and 1.5s
vC (0)
+ -
Circuit at t=0+
di
v L (0 ) L (0 )
dt
vC (0) 12V
AFTER SWITCHING WE HAVE RLC SERIES
d 2iL
R di L
1
(
t
)
(
t
)
i L (t ) 0
2
L dt
LC
dt
DESIRED RESPONSE : i (t ) K1e s1t K 2e s2t ; t 0
Ch. Eq. : s 2 20 s 5 / C ( s s1 )( s s2 ) 0
s1 s2 20; s1s2 5 / C
For the initial conditions analyze circuit
at t=0+. Assume the circuit was in steady
state prior to the switching
INITIAL CONDITIONS :
di
i L (0) 0; v L (0) L L (0) 12
dt
K1 K 2 0
s1K1 s2 K 2 60
60
i L (t )
e s1t e s2t
s2 s1
NOW ONE CAN USE TRIAL AND ERROR
OR CAN ATTEMPT TO ESTIMATE THE
REQUIRED CAPACITANCE
IF FEASIBLE, GET AN IDEA OF THE FAMILY OF SOLUTIONS
Mesh plot
obtained with
MATLAB
» s=[[1:9]';[11:19]'];
» mesh(t,s,ils')
» view([37.5,30])
» xlabel('time(s)'),ylabel('s_1(sec^{-1})')
» title('CURRENT AS FUNCTION OF MODES')
Ils is a matrix that contains all
the computed responses, one
per column
Estimate charge by estimating area under the curve
%example6p14.m
%displays current as function of roots in characteristic equation
% il(t)=(60/(s2-s1))*(exp(-s1*t)-exp(s2*t));
% with restriction s1+s2=20, s1~=s2.
t=linspace(0,5,500)'; %set display interval as a column vector
ils=[]; %reserve space to store curves
for s1=1:19
s2=20-s1;
if s1~=s2
il=(60/(s2-s1))*(exp(-s1*t)-exp(-s2*t));
ils=[ils il]; %save new trace as a column in matrix
end
end
%now with one command we plot all the columns as functions of time
plot(t,ils), grid, xlabel('Time(s)'),ylabel('i(A)')
title('CURRENT AS FUNCTION OF MODES')
For this curve the area is approx. 12 squares
Q 12 0.5 0.5[ A s] 3C
Q 3
C 0.25F 250mF
V 12
s1 s2 20
s1 18.944
s1s2 5 / C 20 s2 1.056
%verification
s1=18.944;
s2=20-s1;
il=(60/(s2-s1))*(exp(-s1*t)-exp(-s2*t));
plot(t,il,'rd',t,il,'b'), grid, xlabel('time(s)'), ylabel('i(A)')
title('VERIFICATION OF DESIGN')
Applications