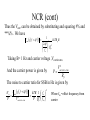Download Microwave Engineering - Universiti Sains Malaysia

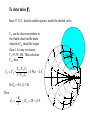
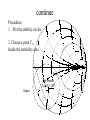
Microwave Oscillator
By
Professor Syed Idris Syed Hassan
Sch of Elect. & Electron Eng
Engineering Campus USM
Nibong Tebal 14300
SPS Penang
One-port negative Oscillator using IMPATT
or Gunn diodes
I
XL
Xin
L
(ZL)
RL
in
(Zin)
Negative
resistance
Rin device
Negative resistance device is usually a biased diode. Oscillation
occurred whence ZL= -Zinwhich implies
L 
Z L  Zo  Zin  Zo Zin  Zo
1



Z L  Zo  Zin  Zo Zin  Zo in
Stability of oscillation
Oscillation takes place when the circuit first unstable, i.e Rin +RL < 0 .
Rin depends on current and frequency. Any transient or noise will excite or
cause oscillation . The oscillation will become stable when Rin +RL=0 and
Xin +XL=0. The stable frequency is fo.
Let’s ZT(I,s)= Zin(I,s) +ZL(s)
Where I current and s=jw is a complex frequency. Then for a small
change in current dI and in frequency ds, the Taylor’s series for
ZT(I,s) is
ZT
Z T  I , s   Z T  I o , so  
s
ZT
ds 
I
so , I o
dI  0
so , I o
Continue (stability)
Use the fact that
ZT I o , so   0
Z T
Z
j T
s
w
Where ds=da+jdw
Therefore
Z T
s
ds 
so , I o
ZT
I
dI  0
so , I o
Z / I
ds  d  jdw  T
Z T / s
dI 
so , I o

 j Z T / I  Z T / w
Z T / w
*
2
 dI
If the transient caused by dI and ds to decay we must have d < 0 when dI>0
so that
 Z T Z T * 
RT X T X T RT

0
Or
subst
Z
=R
+jX
Im 

0

T
T
T
I w
I w
 I w 
Continue ( stability)
For passive load
RL / I  X L / I  RL / w  0
By substituting ZT=Zin + ZL, the stability equation reduces to
Rin   X L  X in  X in Rin

0
I
w
I w
Where Zin = Rin + j Xin
ZL =RL + jXL
Matching diode oscillator
Eg. A negative -resistive diode having Gin=1.25 /40o (Zo=50ohm) at its
desired operating point , for 6 GHz . Design a load matching network for
one-port of 50 ohm load oscillator.
Zin 
1  in
 44  j123 
1  in
Z L   Z in  44  j123 
0.254
50
By plotting ZL in Smith chart
then match to 50 ohm as
50
usual. The
50
 0.308
Diode
Negative
resistance
FET oscillator
Transistor
[S]
Load
network
(tuning)
Terminating
network
L
in
OUT

(Z L)
(Z in)
(Z out)
(Z T)
T
•Choose high degree of unstable device. Typically, common
source or common gate are used.Often positive feedback to
enhance instability.
•Draw output stable circle and choose T for large negative
resistance (I.e Zin). Then take ZL to match Zin. Choose RL
such that RL+Rin < 0, otherwise oscillation will cease.
Design
Usually we have to choose
 Rin
RL 
3
And
X L   X in
For resonation
For steady -state
1
S12 S21T S11  T
 in  S11 

L
1  S22T 1  S22T
where
1  S11L
T 
S22  L
We can proved that
and   S11S22  S12 S21
S12 S21L S22  L
out  S22 

1  S11L 1  S11L
FET common gate
Design 4GHz oscillator using common gate FET configuration
with 5nH inductor to increase instability. Output port is 50. Sparameter for FET with common source configuration are :
(Zo=50) S11= 0.72/-116o, S21=2.6/76o, S12=0.03/57o,S22=0.73/54o.
x2
x1
D
G
ZL
L
in
5nH
y
T
50
50
50
S
50
continue
First we have to convert from common source S-parameter
to common gate with series inductor S-parameter. This is
usually done using CAD. The new S-parameter is given by
S11’= 2.18/-35o, S21’=2.75/96o, S12’=1.26/18o,S22’=0.52/155o.
Thus the output stability circle parameters are given as

CT 

' '* *
  S11
' 2
'2
S22  
'
S22
where
 1.0833o
RT 
' '
' '
'  S11
S22  S12
S21
' '
S12
S21
2
'2
'
S22

 0.665
To determine T
Since S’11>1, thus the stable region is inside the shaded circle.
T can be choose anywhere in
the Smith chart but the main
objective in should be larger
than 1. Let say we choose
T=0.59/-104. Then calculate
in, thus
Stable region
for T
S '12 S '21 T
in  S '11 
 3.96  2.4o
1  S '22 T
Or Zin= -84 - j1.9 
Then
ZL 
 Rin
 jX in  28  j1.9
3
T
Using a transmission line to match a resistive load, thus we have a length
of 0.241  and a load of 89.5 . Using Rin/3 should ensure enough
instability for the startup of oscillator. It is easier to implement ZL =90
ohm . The steady -state oscillation frequency will differ from 4Ghz due to
the nonlinearity of the transistor
For T matching, we can use
open-stub to match 50 ohm. Plot
T and then determine the YT.
Moving towards load until meet
the crossing point between SWR
circle and the unity circle. That the
distant between transistor and the
stub. Obtain the susceptance and
0.319
distance towards open circuit.
D
89.5
L
0.346
in
T
50
G
90ohm
T
50
50
S
50
0.346
Towards generator
0.319
0.241
L
0.241 
Dielectric resonator
Dielectric
resonator
Microstrip
Equivalent series impedance
d
N 2R
Z
1  j 2Qw / w o
Where N =coupling factor/turn ratio
Q=R/woL (unloaded resonator)
wo  1 / LC
w  w  wo
Ratio of unloaded to external Q is given by
where
R / wo L
Q
N 2R
g


RL=2Zo for loaded resistance
2
Qe RL / N w o L 2Z o
= Zo for /4 transmission line
Continue (Dielectric resonator)
Reflection coefficient looking on terminated microstrip
feedline towards resonator is given by
Z

Z
or
2
2


N
R

Z
N
R
g
o
o


2
2


N
R

Z
2
Z

N
R 1 g
o
o
o

g
1 
Q can be determined by simple measurement of reflection
coefficient
Dielectric resonator oscillator
DR
DR
Matching and
terminating
network
Parallel feedback
Zo
Matching and
terminating
network
Series feedback
Zo
Example (dielectric resonator osc.)
Design 2.4GHz dielectric resonator oscillator using series
feedback with bipolar transistor having S-parameters
(Zo=50ohm); S11= 1.8 / 130o , S12= 0.4 / 45o , S21= 3.8 /36o,
S22= 0.7 / -63o. Determine the required coupling coefficient for
dielectric resonator and matching.
Solution
d1
l1
out
d2
/4
L’
L
in
Circuit layout
T
Zo
continue
Procedures
1. Plot the stability circles
2. Choose a point in
Inside the instability area
Input
We choose
in=0.6 /-130 o
Output
continue
Calculate the out and in = L using this formula
out
S12 S 21L
 S 22 
1  S11L
We obtain out = 10.7/132o. This corresponding to
Z out
Then
1  out
1  10.7132o
 Zo
 50
 43.7  j 6.1
o
1  out
1  10.7132
ZT 
 Rout
 jX out  5.5  j 6.1
3
Continue (output matching)
0.431 
0.034 
X
So we have
d1=0.034 l1=0.193 
Or d1=0.429 l1=0.307
Network at resonator
Resonator should be placed at zero or 180o of phase from the
transistor. So we have either 0.181  (zero phase) or 0.431 
(180o phase)
0.431 
d2= 0.181 
Or = 0.431 
Input
We choose
in=0.6 /-130 o
Output
0.181 
Noise in oscillator
•Amplitude noise
•Phase noise
•Flicker noise
Phase noise-may be due to variation of device capacitance
with variation of voltage.This is usually happened in
amplifier.Amplitude noise may be converted to phase
noise if the amplifier is present. Noises cause frequency
instability in oscillator.
Noise to Carrier Ratio (NCR)
Vin
Iout
gm=1/Rp
Vout
P
In
Rp
Lp
Cp
Parallel impedances for Rp , Lp , and Cp can be written as
Z p  jw  
Rp
1  j Q p
where
and
w wo


wo w
Qp  Rp
Cp
Lp

Rp
wL p
NCR Limit (cont)
The transfer function of the oscillator is given by
Vout ( jw )


H jw 

Vin ( jw )
g m Z p ( jw )
1  g m Z p ( jw )
Then substitute for Zp , we have
g m R p ( jw )
Vout ( jw )
H  jw  

Vin ( jw ) 1  jQ p  g m R p ( jw )
At oscillation
w  w o
NCR (cont)
2f
thus  
fo
Where fo=oscillation frequency
And the gain condition (Barkhausen) for oscillation is gmRp=1
Thus, any changes will result
Vout ( j  f  f )
1
1
H  j  f  f  


Vin ( j  f  f )
jQ p j 2f Q
p
fo
#%
NCR (cont)
In the oscillator model, the noise source is Rp .The noise current
produced is
4kTB
In 
Rp
where
k=Boltzman const , T = absolute temp.
B= bandwidth
Since gm= 1/Rp and Iout= gm * Vin , the noise current can be
transferred to input and hence Vin can be written as
Vin ( j ( f  f ))  4kTRp B
**%%
NCR (cont)
Thus the Vout, can be obtained by substituting and squaring #% and
**%% . We have
1
2
Vout  j  f  f  
4kTRp B
2
 2f

 fo
 2
 Q p

Taking B= 1 Hz and carrier voltage ,Vcarrier-rms
2
Vcarrier
 rms
And the carrier power is given by
P
Rp
The noise to carrier ratio for SSB in Hz is given by
No

P
Vout  j  f  f 
2
Vcarrier
 rms
2
kTB 1  f o 
 

2 
P Qp  fm 
2
Where fm =offset frequency from
carrier
NCR (cont)
For phase noise
kTB 1  f o 
 

2 
P
2P Qp  f m 
Np
2
Note: This ratio is half of the total noise since half will be
converted to AM noise and half left for phase noise.
Example
Calculate the phase noise to carrier ratio of an oscillator of 10MHz
with Q=100. Assume the inductor is 2 mH and the peak voltage
across it is 10V. Let the noise figure is 10dB.
f 
1
2 LC
1
1
C
 2
 126 .7 pF
2
6 2
6
2f  L 4 10  10   2  10
1
1
U  CV p2   126.7  1012  102  6.335  109
2
2
Q  wU / Ps
Ps  wU / Q  2fU / Q  2  10  106  6.335  10 9 / 100
 3.98mW  6dBm
kTB 1.38 1023  290 10
NCR 

 5.028 1018  173dB
3
2 Ps
2  3.98 10
Flicker noise ( 1/f noise)
NCR 
kTB  f o 


2 Ps  2Q 
2
 1 
 2 
 fm 
As in previous example
fm
50kHz
30kHz
10kHz
NCR
170dB/Hz
168.5dB/Hz
159dB/Hz
Design for low 1/f noise
Design procedures:1. Choose high Q-factor of the resonator
2. Choose low 1/f noise active components (e.g Bipolar transistor)
3. Choose transistor with the lowest possibility of fT . For good rule
of thumb fT < 2 x fosz .
4. Low current best 1/f performance. Note that fT drops with low
current.
fT 
gm
2Cgs
(FET)
fT 
Maximum oscillation frequency
gm
2C
f max 
For high Q-factor choose parts that have low losses:
1. Resonator
2. Series resistance of capacitors
3. Series resistance of tuning diode
4. PCB.
(HBT)
fT
8 rbCc
(BJT)
Measure phase noise from VNA (for checking)
RF out
HP8714 VNA
1.
2.
3.
4.
5.
6.
7.
8.
HP8594E
Spectrum
Analyzer
Verify power input signal no higher than 10dBm
Reduce input attenuation to minimum (0 dB)
Determine the carrier power at large video and resolution bandwidth at
appropriate span (3MHz RBW, 1MHz VBW,50MHz span.
Set span for single sideband ( desired offset frequency)
Reduce VBW to 10 Hz, RBW to 1 kHz.
Set marker to the carrier. Select marker to show the frequency offset.
Move the marker along the SSB phase noise curve and take reading.

MAX HOLD for maximum phase noise power( let the spectrum settle
for 5 minutes )
Note that cable insertion loss should also be determined
Measure phase noise from VCO
DC power supply
RF out
VCO under
test
22dB adjustable
attenuators
RF out
HP8548C
Signal
Generator
Isolation
Coupled
(-10dB)
Narda 3042-10
Through
HP8594E Spectrum
Analyzer
Input
Reducing Phase Noise in
Oscillators
1. Maximize the Qu of the resonator.
2. Maximize reactive energy by means of a high RF voltage
across the resonator. Use a low LC ratio.
3. Avoid device saturation and try to use anti parallel (back to
back) tuning diodes.
4. Choose your active device with the lowest NF (noise figure).
5. Choose a device with low flicker noise, this can be reduced by
RF feedback. A bipolar transistor with an unby-passed emitter
resistor of 10 to 30 ohms can improve flicker noise by as much as
40 dB. - see emitter degeneration
6. The output circuits should
YIG oscillator
dc magnetic
field
YIG crystal
FET
Matching
section
d1
Load
s
Condition for oscillation
S11’>1 and S22’>1
S22
S11
L
S12 S 21L
S  S 22 
1  S11L
'
22
S12 S 21L
S  S11 
1  S 22L
'
11
YIG equivalent circuit
L1
Co
Ro
Lo
Ro  moVk w mQu
2
Co  1 /(w o Lo )
2
where
fo=resonance frequency=Ho
2
f min  f m
3
Lo  Ro /(w oQu )
Qu 
H o  13 4M s
H
V= volume of YIG sphere
k=1/d1=coupling factor and d1 is the loop diameter
wm= 2fm=2 (4 Ms)
Ho= dc magnetic filed
= gyro magnetic ratio ( 28 GHz/Tesla)
H= resonance line width
L1= self inductance of the loop
4Ms= saturation magnetism
Hartley Oscillator
Colpitts Oscillator
Effects of ambient changes on stability in oscillators
A frequency change of a few tens of hertz back and forth over a
couple of minutes would mean nothing to an entertainment
receiver designed for the FM Radio band. Such a drift in an
otherwise contest grade receiver designed to receive CW (morse
code) would be intolerable. It's a question of relativity.