Download Document

ECE 3336
Introduction to Circuits & Electronics
Note Set #6
Thévenin's and Norton’s Theorems
Spring 2015,
TUE&TH 5:30-7:00 pm
Dr. Wanda Wosik
1
Equivalent Circuits
An equivalent circuit is used to simplify the original circuit
however, at the terminals, it maintains the exact same
parameters: ex. voltage and current.
Here, equivalent circuits are used to simplify circuit interaction
with the load (ex. another circuit, resistors, other passive
elements etc.)
• Thevenin Equivalent
• Norton Equivalent
2
Equivalent Circuits
Reminder: The same circuit but different equivalent circuit at different points
• All elements to the right of VS2 are replaced by equivalent circuit D.
• Currents i0=iD are the same
• Voltages V2&V3 lost their meanings but VD is the same.
Equivalent
circuit
i0
iD
D
A
VD
B
VD
}
}
This part of the circuit must not “notice” any change on the right.
3
Thévenin’s Theorem
Thévenin’s Theorem: any circuit built of sources and resistors can be represented by
one voltage source (Thevenin Voltage) and a resistance in series (Thevenin
Resistance).
Source Circuit drives Load Circuit
The voltage source is equal to the open-circuit voltage voc=vT
The resistance is equal to the equivalent resistance RT of the circuit.
4
Thevenin Equivalent Voltage VTH
and Resistance RTH
vTH = open-circuit voltage, and
Thevenin equivalent is obtained
by finding voc and RTH
RTH = equivalent resistance.
To find voc we have to first disconnect the load.
RTH
A
Any circuit
made up of
resistors and
sources
Rload
vOC=vTH
vTH
~
B
A
Rload
+
B
Now, we can
calculate
power
delivered to
the load,
voltage,
current.
5
Polarity of the voltage source
The polarities the Thevenin voltage source must be the same as
open circuit voltage vOC.
vTH = open-circuit voltage, and
RTH = equivalent resistance.
No load
here
Rload
Thevenin equivalent will have identical properties as the original
circuit, when we connect the load Rload
6
Zeroing Current and Voltage Sources
This is Source Deactivation
7
Equivalent resistance RTH
Equivalent Resistance: it is in series with the Thevenin voltage
source in the equivalent circuit.
• Set independent sources equal to zero.
• Any dependent sources are left in place.
Shorted
source
RTH
Disconnect
the load
8
Short Circuit Current iSC
HERE:
isc ≠ zero
~
isc
Open
Circuit voltage
vTH ~ vOC
RTH ~ REQ
Short
Circuit current
vOC = iSC REQ .
It is not Ohm’s Law
The polarities of the short circuit current
as in Ohm’s Law
Finding the Thévenin Equivalent
To find the Thévenin equivalent of a circuit by finding
any two of the following three things:
1) the open circuit voltage, vOC,
2) the short-circuit current, iSC, and
3) the equivalent resistance, REQ.
Once we find any two, we can
find the third by using this equation.
REQ
+
vOC
+
-
iSC
vOC
vOC = iSC REQ .
vOC = vTH,
A
and
-
REQ = RTH.
iSC
If you change the signs
vOC = -iSC REQ .
B
10
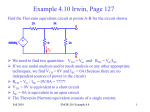
Example #1
Find Thévenin equivalent of the circuit below, as seen from
terminals A and B (RL will be connected there later).
Use Node Voltage Method
R1=
22[W]
R2=
33[W]
A
+
+
vS =
100[V]
+
iS=
4[A]
vC
R3=
10[W]
R4=
15[W]
vOC
-
-
-
⏏
vC
vC
vC - vS
+ - iS +
= 0.
R2 + R4 R3
R1
B
0.1663[S]vC = 4[A]+ 4.545[A]
vC = 51.4[V].
11
Find Thevenin Voltage
For Thévenin equivalent having found vC we will find vOC
from the voltage divider rule
R1=
22[W]
R2=
33[W]
A
+
+
vS =
100[V]
+
iS=
4[A]
vC
R3=
10[W]
R4=
15[W]
vOC
-
-
B
-
⏏
vC = 51.4[V]
vOC
vOC
15[W]
= vC
. Solving, we get
15[W]+ 33[W]
= 16[V].
12
Find Thevenin Resistance
Independent sources are deactivated i.e. equal to zero.
Resistance seen from the output terminals (A & B) is calculated
R1=
22[W]
R2=
33[W]
R3=
10[W]
A
R4=
15[W]
B
REQ = {(R1 || R3 ) + R2 }|| R4 = {(22[W] ||10[W]) + 33[W]}||15[W]. Solving, we get
REQ = 10.9[W].
13
Thevenin Equivalent Found
RTH=REQ=
10.9[W]
vTH=
16[V]
vTH=
16[V]
-
A
+
-
B
vTH = iSC RTH
RTH=REQ=
10.9[W]
A
+
We can also find isc
Now, Short Circuit Current
B
vTH
16[V]
iSC =
=
= 1.5[A].
REQ 10.9[W]
14
Find Short Circuit Current (compare)
Short-circuit current in the original circuit – node voltage IS CHANGED.
vD
vD
vD - 100[V]
+
- 4[A] +
= 0. Solving, we get
33[W] 10[W]
22[W]
The same
0.1758[S]vD = 4[A] + 4.545[A], or
value as
vD
48.6[V]
iSC =
=
= 1.5[A] from VTH
vD = 48.6[V].
and RTH
33[W] 33[W]
R1=
22[W]
R2=
33[W]
+
vS =
100[V]
+
iS=
4[A]
vD
A
isc
R3=
10[W]
R4=
15[W]
-
-
B
15
Norton’s Theorem
Norton’s Theorem: any circuit built of sources and resistors can be
represented by one current source (Thevenin Current ) and a resistance in
parallel (Thevenin Resistance).
A
-
Source Circuit drives Load Circuit
The current source is equal to the short circuit
current isc=iN
The resistance RN is equal to the equivalent
resistance RT of the circuit.
iN
iN =
iSC
RN vOC
+
B
16
Norton’s Theorem
iN = short-circuit current
RN = equivalent resistance.
Norton equivalent is obtained by
finding isc and RTH
To find iSC we have to first disconnect the load
We can also find iSC from the
vTH = iSC RTH
A
A
iSC
Rload
iN
Any circuit
made up of
resistors and
sources
~
B
iRN=0
RN
iN = iSC
iN Norton Current
iSC
B
17
Finding the Norton Equivalent
We can find the Norton equivalent of a circuit by finding
any two of the following three things:
1) the open circuit voltage, vOC,
vOC=vTH
2) the short-circuit current, iSC, and
iSC = iN
3) the equivalent resistance, REQ.
REQ = RN.
Once we find any two, we can
find the third by using this equation,
A
vOC = iSC REQ .
Any circuit
made up of
resistors and
sources
A
~
B
iN
RN
B
18
Norton Equivalent - equivalent Behavior
vOC = vTH = open-circuit voltage,
iSC = iN = short-circuit current, and
RTH = RN = equivalent resistance.
Dependent sources
in the circuit do not
change the validity of
the theorem.
These sources
cannot be
deactivated though.
A
+
Any circuit
made up of
resistors and
sources
A
iSC
Pick
vOC
~
polarity
-B
iN
RN
B
Polarity of current iN important; as in Ohm’s Law
It is NOT Ohm’s Law (different circuit)
19
Example #1
Find the Norton equivalent of the circuit below, as seen from
terminals A and B (here the load will be connected). All resistors
belong to the circuit.
Use NVM to find vOC.
(
)
vOC 0.1095[S] = 2[A], or
vOC
vOC vOC - vS
+
+
= 0.
R5 + R4 R3
R2
vOC = 18.3[V].
R2=
27[W]
R1=
39[W]
R5=
27[W]
A
+
iS=
9[A]
vS =
54[V]
+
-
R3=
22[W]
vOC
R4=
10[W]
B
20
Equivalent Resistance RN
To find the equivalent resistance, REQ we deactivate all
sources= set them to zero.
(
)
REQ = R5 + R4 || R2 || R3 = 37[W] || 27[W] || 22[W]
REQ = 9.13[W].
The voltage source
becomes a short
circuit, and the
current source
becomes an open
circuit.
R1=
39[W]
R2=
27[W]
R5=
27[W]
A
R3=
22[W]
B
R4=
10[W]
21
Norton Equivalent Found
The complete Norton’s equivalent, seen from
terminals A and B has iN and RN
A
vOC = iN REQ
vOC 18.3[V]
iN =
=
= 2.00[A].
REQ 9.13[W]
iN=
2.00[A]
REQ=RN=
9.13[W]
B
22
Norton Equivalent: iSC
Find the short-circuit current in the original circuit directly not though vTH.
R2=
27[W]
R1=
39[W]
iS=
9[A]
vS =
54[V]
A
i(R4+R5)=0
iR3=0
+
-
R5=
27[W]
R3=
22[W]
iSC
R4=
10[W]
B
23
Redraw the Circuit
Calculate iSC
from the
modified circuit
iSC
vS 54[V]
=
=
. Solving, we get
R2 27[W]
iSC = 2.00[A].
Norton Equivalent
R2=
27[W]
R1=
39[W]
iS=
9[A]
vS=
54[V]
A
A
iSC=
iN=
2.00[A]
+
iSC
REQ=RN=
9.13[W]
-
B
B
24
Measurement of open-circuit voltage and
short-circuit current
Figur
e
3.67
Simplification of
R–2R ladder
circuit
Copyright ©2005 by Pearson Education, Inc.
Upper Saddle River, New Jersey 07458
All rights reserved.
26
Source
transformation
27
Source transformation
Norton equivalent circuit
28
Summary
1. Thevenin and Norton equivalents of any circuit made up of voltage sources,
current sources, and resistors are very important in complicated circuits.
2. We can find the values of the these equivalents by finding two of three
parameters: the open-circuit voltage, short-circuit current or equivalent resistance.
The reference polarities of these quantities are important.
3. To find the equivalent resistance, we need to set the independent sources
equal to zero. However, the dependent sources will remain.
29
Superposition Principle
The total current (through) or total voltage (across) any part of a
linear circuit is the algebraic sum of all currents/voltages
produced by each source acting separately.
30
Superposition Principle
• All independent sources must be deactivated i.e. zeroed:
V=0 (short), I=0 (open) except for ONE.
• Do not turn off dependent sources
• Repeat calculations for every independent source in the circuit
• Add all obtained values of currents and voltages to find their total
values.
http://hyperphysics.phy-astr.gsu.edu/hbase/electric/suppos.html#c2
31