* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Distance - courses.psu.edu
Cassiopeia (constellation) wikipedia , lookup
Extraterrestrial life wikipedia , lookup
Star of Bethlehem wikipedia , lookup
Cygnus (constellation) wikipedia , lookup
Observational astronomy wikipedia , lookup
Rare Earth hypothesis wikipedia , lookup
Dyson sphere wikipedia , lookup
History of Solar System formation and evolution hypotheses wikipedia , lookup
Formation and evolution of the Solar System wikipedia , lookup
Solar System wikipedia , lookup
Stellar evolution wikipedia , lookup
Perseus (constellation) wikipedia , lookup
Geocentric model wikipedia , lookup
Astronomical spectroscopy wikipedia , lookup
Tropical year wikipedia , lookup
Extraterrestrial skies wikipedia , lookup
Planetary habitability wikipedia , lookup
Malmquist bias wikipedia , lookup
Corvus (constellation) wikipedia , lookup
Dialogue Concerning the Two Chief World Systems wikipedia , lookup
Aquarius (constellation) wikipedia , lookup
Cosmic distance ladder wikipedia , lookup
Timeline of astronomy wikipedia , lookup
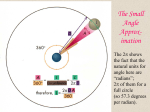
Distance Outline 1. Getting Distances to Stars * Geometry: Stellar Parallax * Inverse-Square Law: F L 4 d 2 2. Stellar Parallax * Parallax effect * Triangulation: d 1 p * Parsec 3. Luminosity * Total energy radiated per second: watts 4. Brightness * Flux: light energy flowing per second per sq meter: watts/m2 * Derivation of the inverse-square law * Flux (F) & distance (d) ==> luminosity * Sun' flux at Earth (1370 W/m2) ==> solar luminosity Questions 1. Ques. #3, pg. 268. 2. What does a star's flux measure? 3. a) A star with the Sun's luminosity, but located 2 AU from Earth instead of 1 AU, would appear how bright relative to the Sun? b) A star with the Sun's luminosity, but located 20 AU from Earth instead of 1 AU, would appear how bright relative to the Sun? 4. Jupiter's moon Europa, which effectively lies at the same distance from the Sun as Jupiter (5.2 AU) receives how much sunlight per square meter, relative to the amount received by Earth? 5. a) In the distant future, the sun will likely become 100 times more luminous than at present (when it expands to become a 'giant star'). What will be the solar flux (in watts/m2) at Earth at that time? b) How far from the sun would we have to move so that the sun's flux would be equal to its present value? 6. A certain star is known to be equal in luminosity to the Sun, but its measured flux is only 1/10,000 (one ten-thousandth) the Sun's flux. What would be the distance to this star, in AU? 7. Two stars, A and B, are known to be equal in luminosity, but A appears 16 times brighter (as viewed from Earth) than B. Which one is more distant, and how much farther away is it than the other? 8. Tripling the luminosity of the star Sirius while also tripling its distance from Earth would have what effect on its apparent brightness, as viewed from Earth? 9. Ques. #7, pg. 268. 10. Prob. #1, pg. 268. 11. a) What is the parallax of Betelgeuse, which lies at a distance of 130 pc from the Sun? b) Would Betelgeuse's parallax change significantly were we to measure its distance from Earth, instead of "from the Sun," as we do in part a) of this question? Explain your answer. 12. Why do stellar parallax measurements work only with nearby stars? Answers 1. Luminosity measures the total energy radiated by the star per second, at all wavelengths. The standard luminosity unit is the watt. The luminosity of a star in units of L tells us how luminous the star is relative to the Sun. For example: a star with luminosity 0.25 L would be one-quarter the Sun's luminosity. 2. Flux is a measure of the amount of energy flowing per second through a unit area (e.g., one square meter) due to a star (or any other luminous source). 3. a) This star would appear 1/4 as bright as the sun; i.e., its flux would be 1/4 the sun's flux: 2 F2 d1 12 1 2 2 F1 4 2 d2 b) The star would appear 1/400 as bright as the Sun: 2 F2 d 12 1 12 2 F1 400 20 d2 4. 2 F2 d 12 1 12 2 F1 27 5.2 d2 So, Europa receives about 1/27 as much solar energy per square meter as does Earth. 5. The flux will be 100 times greater, because (for no change in distance), flux is directly proportional to luminosity: F F L L 100 2 2 100 2 F1 L1 1 4 d At Earth, the current flux is 1370 W/m2; so, when the Sun becomes 100 times more luminous, the flux will be 100 * 1370 = 137,000 W/m2. Wow! Lotsa wattsa. 6. d2 2 d1 2 2 F d 10,000 1 22 d 2 10,000 100 AU F2 1 1 7. dA 2 dB 2 FB d 1 A FA 16 dB 1 1 16 4 So, to appear 16 times brighter, Star A must be 4 times closer. 8. F2 L 2 d1 L 3 12 3 1 F 2 2 2 F1 9 3 4 d 1 3 L1 d 2 2 So, Sirius would appear 1/3 as bright. 9. This is very simple: The distance (d) is related to the parallax angle (p), by this formula d 1 p p must be measured in arcseconds, so that d is in parsecs (pc); 1 pc = 3.26 ly. 10. d 1 1 1.35 pc 4.40 ly p 0.742 d 1 3.50 pc 11.4 ly 0.286 p 1 1 0.00769 arcsec d 130 11. a) b) Parallax would change by a tiny amount because – at best – 1 AU would be added to or subtracted from 130 pc, and there are 206, 265 AU in 1 pc! So, like, the difference is miniscule, dude. 12. Stellar parallax measurements work only for nearby stars because, as distance increases, parallax angle increases. At a distance which isn’t very big (about 100 pc), the angle (in this case, 0.01 arcsec) becomes too small to measure accurately.