Download Nessun titolo diapositiva

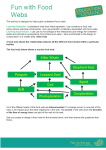
DYNAMICS OF COMPLEX SYSTEMS
Self-similar phenomena and Networks
Guido Caldarelli
CNR-INFM Istituto dei Sistemi Complessi
[email protected]
6/6
•STRUCTURE OF THE COURSE
1.
SELF-SIMILARITY (ORIGIN AND NATURE OF POWER-LAWS)
2.
GRAPH THEORY AND DATA
3.
SOCIAL AND FINANCIAL NETWORKS
4.
MODELS
5.
INFORMATION TECHNOLOGY
6.
BIOLOGY
•STRUCTURE OF THE FIRST LECTURE
6.1) PROTEIN INTERACTION NETWORKS
6.2) FOOD WEBS
6.3) FOOD WEBS:Optimisation
6.4) PLANT TAXONOMIES
•6.1 PROTEIN INTERACTION NETWORK
Network of Interaction for the protein of Baker’s Yeast (Saccharomyces Cerevisiae)
•6.1 PROTEIN INTERACTION NETWORK
How do growth and preferential attachment
apply to protein networks?
• Growth: genes (that encode proteins) can be,
sometimes, duplicated; mutations change
some of the interactions with respect
to the parent protein
• Preferential attachment: the probability that a protein
acquires a new connection is related to the
probability that one of its neighbors is
duplicated; proportional to its connectivity
A. Vazquez et al., ComPlexUs 1, 38-44 (2003)
•6.1 PROTEIN INTERACTION NETWORK
The two hybrid method way of detecting protein interactions
•6.1 PROTEIN INTERACTION NETWORK
With the solvation free energies taken from an exponential probability
distribution p(f) = e-f, we obtain
P(k) ~ k-2
• The real network is random
• The detection method sees
only pairs with large enough
binding constants
• The binding constant is related
to the solubilities of the two
proteins
• Solubilities are given
according to some distribution
•6.2 FOOD WEBS
sequence of predation relations among different living
species sharing the same physical space (Elton, 1927):
Flow of matter and energy from prey to predator, in more
and more complex forms;
The species ultimately feed on the abiotic environment
(light, water, chemicals);
At each predation, almost 10% of the resources are
transferred from prey to predator.
•6.2 FOOD WEBS
Set of interconnected food chains resulting in a much more complex topology:
•6.2 FOOD WEBS: The topology
Trophic Species:
Set of species sharing the same set of preys and the same
set of predators (food web  aggregated food web).
Trophic Level of a species:
Minimum number of predations separating it from the
environment.
Basal Species:
Species with no prey (B)
Top Species:
Species with no predators (T)
Intermediate Species:
Species with both prey and
predators ( I )
Prey/Predator Ratio =
BI
IT
•6.2 FOOD WEBS: The topology


Pamlico Estuary
(North Carolina):
14 species
Aggregated Food Web of
Little Rock Lake (Wisconsin)*:
182 species  93 trophic species
How to characterize the topology of Food Webs?
Graph Theory
* See Neo Martinez Group at http://userwww.sfsu.edu/~webhead/lrl.html
•6.2 FOOD WEBS: The degree
irregular
or scalefree?
P(k) k-
R.V. Solé, J.M. Montoya Proc. Royal Society Series B 268 2039 (2001)
J.M. Montoya, R.V. Solé, Journal of Theor. Biology 214 405 (2002)
•6.2 FOOD WEBS: The spanning tree
A spanning tree of a connected directed graph is any of its connected directed
subtrees with the same number of vertices.
The same graph can have more spanning trees with different topologies.
Since the peculiarity of the system (FOOD WEBS),some are more sensible
than the others.
•6.3 FOOD WEBS: The Optimisation
1
1
w
XY
13
5
Out-component size:
AX 
1 1
AY 1
0,5
1
11 2 3
22 1
Sum of the sizes:
CX 
1
A

 
Y
Y
X
Allometric relations:
Out-component size
distribution P(A) :
0,6
1
5
8
Y nn X
1
10
33
CX  CX A X  
35
P(A)
C  C A
C(A)
30
33
0,5
25
0,4
22
20
0,3
15
0,2
11
10
0,1
0,1
0,1
0,1
0,1
0,1
5
A
0
1
2
3
4
5
6
7
8
9
10
5
A
3
1
0
0
2
4
6
8
10
12
•6.3 FOOD WEBS: The Optimisation
A0: metabolic rate B
C0: blood volume ~ M
Kleiber’s Law:
B(M)  M 3 / 4
C( A )  A 

General Case (tree-like transportation system
embedded in a D-dimensional metric space):
D1
the most efficient scaling is C( A )  A   
D
West, G. B., Brown, J. H. & Enquist, B. J. Science 284, 1677-1679 (1999)
Banavar, J. R., Maritan, A. & Rinaldo, A. Nature 399, 130-132 (1999). |
4
3
•6.3 FOOD WEBS: The Optimisation
AX: drained area of point X
Hack’s Law:
C( A )  A 
L  A0.6

3
2
•6.3 FOOD WEBS: The Optimisation
•6.3 FOOD WEBS: The Optimisation
(D.Garlaschelli, G. Caldarelli, L. Pietronero Nature 423 165 (2003))
•6.3 FOOD WEBS: The Optimisation
Little Rock
Webworld
Little Rock
Webworld
S
182
182
S
93
93
L
2494
2338
L
1046
1037
B
0.346
0.30
B
0.13
0.15
I
0.648
0.68
I
0.86
0.84
T
0.005
0.02
T
0.01
0.01
Ratio
1.521
1.4
Ratio
1.14
1.16
lmax
3
3
lmax
3
3
C
0.38
0.40
C
0.54
0.54
D
2.15
2.00
D
1.89
1.89

1.11±0.03
1.12±0.01

1.15±0.02
1.13±0.01

2.05±0.08
2.00±0.01

1.68±0.12
1.80±0.01
Original Webs
Aggregated Webs
•6.3 FOOD WEBS: The Optimisation
  1
0 1
 0
C( A)  A
efficient
C(A)  A 1    2
P(A)   A1
stable
P(A)  A  0    
C( A)  A 2
inefficient
P(A)  cost
unstable
•6.4 PLANT TAXONOMIES
Lazio
Utah
Peruvian
and Atacama
Desert
Amazonia
Iran
Argentina
Ecosystem = Set of all living
organisms and environmental properties of
a restricted geographic area
we focus our attention on plants
in order to obtain a good universality of the results we have
chosen a great variety of climatic environments
•6.4 PLANT TAXONOMIES
Linnean Tree = hierarchical structure organized on different
levels, called taxonomic levels, representing:
•
•
classification and identification of different plants
history of the evolution of different species
phylum
subphylum
class
subclass
order
A Linnean tree already has
the topological structure of a tree graph
family
genus
species
• each node in the graph represents a different taxa
(specie, genus, family, and so on). All nodes are
organized on levels representing the taxonomic one
• all link are up-down directed and each one
represents the belonging of a taxon to the relative
upper level taxon
Connected graph without loops or
double-linked nodes
•6.4 PLANT TAXONOMIES
P(k)
Degree distribution:
k
P ( k )  k 
 ~ 2.5  0.2
The best results for the exponent value are given by ecosystems
with greater number of species. For smaller networks its value can
increase reaching  = 2.8 - 2.9.
•6.4 PLANT TAXONOMIES
Colosseo
(Terza Università, Rome)
 6 historical periods
(1643 - 2001)
 historical events
 climatic changes
Valmalenco (Bernina)
(University of Pavia)
(G. Rossi, M. Gandini)
 3 historical periods
(1949 - 2003)
 climatic changes
(Global Warming)
•6.4 TAXONOMY: Real Subsets
Tiber
Mte Testaccio
Aniene
Lazio
k
 =2.52  0.08
City of Rome
Colli Prenestini
k
 =2.58  0.08
k
2.6 ≤  ≤ 2.8
•6.4 TAXONOMY: Random Subsets
P(k)
P(k)
P(k)
random extraction of 100, 200 and 400 species between those belonging
to the big ecosystems and reconstruction of the phylogenetic tree
ROME
LAZIO
k
P(k)
P(k)
• Simulation:
k
k
P(k)=k -2.6
k
k
•6.4 TAXONOMY: Random Subsets
P(kf, kg) that a genus with degree kg belongs to a family with degree kf
kf=1
kf=2
kf=3
kf=4
 kg = ∑g kg P(kf,kg)
fixed
P(kf,kg) kg -
fixed
 ~ 2.2  0.2
kf
kg
P(ko,kf) that a family with degree kf belongs to an order
ko=1
ko=2
ko=3
ko=4
P(ko,kf) kf
 kf = ∑f kf P(ko,kf)
fixed
-
fixed
 ~ 1.8  0.2
kf
with degree ko
ko
•6.4 TAXONOMY: Random Subsets
1)
create N species to build up an ecosystem
2)
Group the different species in genus, the genus in families, then families
in orders and so on realizing a Linnean tree
- Each species is represented by a string with 40 characters representing 40
properties which identify the single species (genes);
- Each character is chosen between 94 possibilities: all the characters and
symbols
that in the ASCII code are associated to numbers from 33 to 126:
P g H C ) %o r ? L 8 e s / C c W & I y 4 ! t G j
z AB
4 2£ ) k , ! d q 2= m: f V
Two species are grouped in the same genus according
to the extended Hamming distance dWH:
c1i = character of species 1
c2i = character of species 2
ba Z
with i=1,……….,40
with i=1,……….,40
dEH = ( ∑i=1,40 |c1i - c2i| )/40
•6.4 TAXONOMY: Random Subsets
P g H C ) %o r ? L
G j
4 2£ ) k , ! d
dEH ≤ C
|c1i - c2i| = 17
species 1
same genus
Fixed threshold
species 2
genus = average of all species belonging to it
c14
c(g)4
P g H C ) %o r ? L
( c1i + c2i )/2
G j
:
4 2£ ) k , ! d
c24
Same proceedings at all levels with a fixed threshold for each one
At the last level (8) same phylum for all species (source node)
•6.4 TAXONOMY: Random Subsets
No correlation: species randomly created with no
relationship between them
Genetic correlation: species are no more independent but
descend from the same ancestor
• No correlation:
 ecosystems of 3000 species
 each character of each string is chosen
at random
 quite big distance between two different
species:
P(k)
dEH ~ 20
(S . ` U d ~j <@a ~N f K Mg X w´ * : * 4 " j ° z G 9 / F y 2 J ´ R _ x 5
K L ` < G ´ D Q b mV U W ; d L U x o g Z k * 8 y u N v D K Z + { C x 6 I 6 d z
k
(top ~ 1.7  0.2
bottom ~ 3.0  0.2 )
•6.4 TAXONOMY: Random Subsets
 single species ancestor of all species in the ecosystem
 at each time step t a new species appear:
- chose (randomly) one species already present in the ecosystem
- change one of its character
 3000 time steps
Environment = average of all species present in the
natural selection
the ecosystem at each time step t.
 At each time step t we calculate the distance between
the environment and each species:
dEH < Csel
survival
dEH > Csel
extinction
 small distance between different species:
dEH ~ 0.5
g 5 0 _ " & y = E o [ l R C ( x z G ? g = X %W @ @ / X r ] T K g ? 6 Y G ^ Q z
g 5 0 _ " & y = E o [ : R C ( x z G ? 0 = / %W ´ S / X r ] T K g ? 6 K ^ ^ Q z
P(k) ~ k -
k
 ~ 2.8  0.2
•6.4 TAXONOMY: Random Subsets
Correlated:
k
k
P(k)
Not Correlated:
•CONCLUSIONS
Results:
 networks (SCALE-FREE OR NOT) allow to detect universality
(same statistical properties) for FOOD WEBS and TAXONOMY.
Regardless the different number of species and environment
 STATIC AND DYNAMICAL NETWORK PROPERTIES other than
the degree distribution allow to validate models.
NEITHER RANDOM GRAPH NOR BARABASI-ALBERT WORK
Future:
 models can be improved with
particular attention to environment and natural selection
FOR FOOD WEBS AND TAXONOMY
 new data
COSIN
COevolution and Self-organisation In
dynamical Networks
RTD Shared Cost Contract IST-2001-33555
http://www.cosin.org
•
•
•
•
•
Nodes
Period of Activity:
Budget:
Persons financed:
Human resources:
EU countries
Non EU countries
EU COSIN participant
Non EU COSIN participant
6 in 5 countries
April 2002-April 2005
1.256 M€
8-10 researchers
371.5 Persons/months