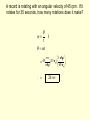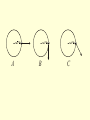Download File

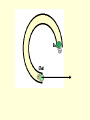
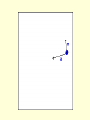
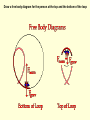
Motion in a Circle
Uniform Circular Motion
Motion of an object in a circle with uniform or
constant speed.
Examples???
Angular Velocity
The angular velocity is the rate of change in angular displacement.
angular displacement
angular velocity 
time


t
rev
min
(Common
everyday
language)
rad s-1
(physics
language)
A record is rotating with an angular velocity of 45 rpm. If it
rotates for 35 seconds, how many rotations does it make?

 1 min 
rev

  t 45
 35 s  

t
min
60 s 

 1 min 

rev

  t 45
2
 35 s  
 
t
min
 60 s 
 1 min 
 1 min 
rev
rev





t
45
35
s
26 rev
  t 45
26 rev 
 35 s  
 
 
  t
t s
 60

 1 min 
rev
45
 35 s  
 
min
 60 s 
min
min
26 rev
 60 s 
Linear Velocity
Assume it takes Sammy Speedster T
seconds to drive one complete revolution
around the circle with a radius of R. Draw
his velocity vector at 2 different locations
and label the vector with the speed he is
traveling.
(T = Period = the amount of time it takes for
an object to complete one revolution.)
Velocity
Does Sammy’s speed change with time?
Does Sammy’s velocity change with time?
What does that mean for Sammy’s acceleration?
Are there any forces acting on Sammy?
In which direction are they acting?
(A tangent line is a line which touches a circle at one
point but does not intersect it.)
To summarize, an object moving in uniform
circular motion is moving around the
perimeter of the circle with a constant
speed. While the speed of the object is
constant, its velocity is changing. Velocity,
being a vector, has a constant magnitude
but a changing direction. The direction is
always directed tangent to the circle and
as the object turns the circle, the tangent
line is always pointing in a new direction.
A
B
C
The velocity and acceleration vectors are perpendicular to each other.
This causes the velocity vector to change direction, but not magnitude.
An object is moving in a clockwise direction
around a circle at constant speed.
A
1. Draw and label the velocity vector
at each point.
2. Draw and label the acceleration
vector at each point
B
C
A 900-kg car moving at 10 m/s takes a turn around a
circle with a radius of 25.0 m. Determine the
acceleration and the net force acting upon the car.
a = v2 / R
a = (10.0 m/s)2 / (25.0 m)
a = (100 m2/s2) / (25.0 m)
a = 4 m/s2
Fnet = m • a
Fnet = (900 kg) • (4 m/s2)
Fnet = 3600 N
A 95-kg halfback makes a turn on the football field. The halfback sweeps out
a path which is a portion of a circle with a radius of 12-meters. The halfback
makes a quarter of a turn around the circle in 2.1 seconds. Determine the
speed, acceleration and net force acting upon the halfback.
v=d/t
v = (0.25 • 2 • pi • R) / t
v = (0.25 • 2 • 3.14 • 12.0 m) / (2.1 s)
v = 8.97 m/s
Fnet = m*a
Fnet = (95.0 kg)*(6.71 m/s2)
Fnet = 637 N
a = v2 / R
a = (8.97 m/s)2 / (12.0 m)
a = (80.5 m2/s2) / (12.0 m)
a = 6.71 m/s2
945-kg car makes a 180-degree turn with a speed of 10.0
m/s. The radius of the circle through which the car is
turning is 25.0 m. Determine the force of friction acting
upon the car.
F = mv2/R
F = (945kg)(10.0m/s)2/25.0m
F = 3780 N
The roller coaster
Draw a free body diagram for the person at the top and the bottom of the loop
Suggested Method of Solving Circular Motion Problems
1. construct a free-body diagram. Represent each force by a vector arrow
and label the forces according to type.
2. Identify the given and the unknown information (express in terms of
variables such as m= , a= , v= , etc.).
3. If any of the individual forces are directed at angles to the horizontal
and vertical, then resolve such forces into horizontal and vertical
components.
3. Determine the magnitude of any known forces and label on the freebody diagram.
(For example, if the mass is given, then the Fgrav can be determined)
4. Use circular motion equations to determine any unknown information.
(For example, if the speed and the radius are known, then the
acceleration can be determined. And as another example, if the period
and radius are known, then the acceleration can be determined.)
5. Use the remaining information to solve for the requested information.
If the problem requests the value of an individual force, then use the
kinematic information (R, T and v) to determine the acceleration
and the Fnet ; then use the free-body diagram to solve for the
individual force value.