* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download The Wave Equation & Velocity
Monte Carlo methods for electron transport wikipedia , lookup
Brownian motion wikipedia , lookup
Analytical mechanics wikipedia , lookup
Shear wave splitting wikipedia , lookup
Four-vector wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Hooke's law wikipedia , lookup
Derivations of the Lorentz transformations wikipedia , lookup
Fluid dynamics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Wave packet wikipedia , lookup
Centripetal force wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Routhian mechanics wikipedia , lookup
Work (physics) wikipedia , lookup
Spinodal decomposition wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Surface wave inversion wikipedia , lookup
Classical central-force problem wikipedia , lookup
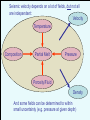
Geology 5640/6640 30 Jan 2015 Introduction to Seismology Last time: The Equations of Motion (Wave Equation!) • Any imbalance of stress will be offset by acceleration (Newton’s 2nd: F ma). This leads to the dynamic equations of motion: Ýi j ij fi uÝ • We neglect the body force fi (for now) and express in terms of displacement, by substituting Hooke’s law and the definition of the strain tensor. This results in the equation: P-wave 2 2 2 2 t in which is the propagation velocity: 2 2 2 u u 2 t 2 Read for Mon 2 Feb: S&W 53-62 (§2.4); 458-462 © A.R. Lowry 2015 This is the wave equation for dilatations only (i.e., a P-wave!) and is more commonly written: 2 2 2 2 t where: 2 represents the propagation velocity! (Note the units: sqrt(Pa (kg m-3)-1) = sqrt (kg m-1 s-2 kg-1 m3) = sqrt (m2/s2) or just m/s). If we recall moreover that u u u 1 2 3 u x1 x 2 x 3 We can write in terms of displacement as: 2 2 2 u u 2 t We arrived at the P-wave equation using 2 ui 2 2 u i x i t by taking the derivative with respect to xi and summing over i. We could instead take derivatives with respect to xj and set of steps arrive at: by a similar 2 2 2 u u 2 t the S-wave equation, in which the S-wave propagation velocity is given by Note the important implication: For the P-wave we have dilatation, but no shear; for the S-wave we have shear, but no dilatation! 2 • Here and represent the propagation velocities for the P and S waves respectively. • Changes in elastic properties contribute more to velocity variation than changes in density • Velocity is sensitive to rock chemistry, packing structure, porosity & fluid type, pressure and temperature. The tricky part is distinguishing which we’re seeing… Rock properties that affect seismic Crustal Rocks velocity include: • Porosity • Rock composition • Pressure • Temperature • Fluid saturation = Vp, = Vs are much more sensitive to and than to Mantle Rocks Seismic velocity depends on a lot of fields, but not all are independent: Velocity Temperature Composition Partial Melt Pressure Porosity/Fluid Density And some fields can be determined to within small uncertainty (e.g. pressure at given depth) So now we have our expressions for the wave equation in terms of displacements: 2 2 2 u u 2 t 2 2 2 u u 2 t Question is, how do we solve these? expressing displacements u Solution is simplified by in terms of displacement potentials. Helmholtz’ decomposition theorem holds that any vector field u can be expressed in terms of a vector potential and a scalar potential as: u In our application, is a scalar displacement potential associated with the P-wave, and is a vector displacement potential associated with the S-wave. It’s first worth noting a pair of useful vector identities: 0 0 Then, if we substitute our potentials into our P-wave equation: 2 2 2 2 t Rearranging: 2 2 2 2 0 t 2 And hence: 1 2 2 t 2 2 Similarly, substituting potentials into the S-wave equation: 2 2 2 2 t Here we take advantage of another vector identity: 2 2 Rearranging: 2 2 2 2 0 t 2 And hence: 1 2 2 t 2 2 So what’s the point of this? We want to find some solution, e.g. for P-wave displacement potential, that allows for separation of variables: x,t Xx1Y x2 Zx3 T t The eigenfunctions for a partial differential equation of this form (i.e., functions which, if plugged into the equation, will yield solutions of similar form) are: x ,t Ae i t k x (called the “d’Alembert solution”). Here, i is the imaginary number 1 A is amplitude is angular frequency 2/T (& T is time period) k is spatial wavenumber 2/ (& is wavelength)