Download Escape Velocity

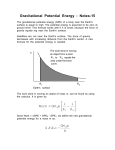
Escape Velocity
Escape Velocity
 In order to get to the moon, you have to escape the gravity of the earth.
To get past Pluto you have to escape the gravity of the sun. The escape
velocity of the earth is 11.2 km/s or 25,000 mi/h.
 The escape velocity of the sun at the earth’s surface is 42.1 km/s or 94,000
mi/hr. The Saturn V rocket—one of the largest rockets ever built which
blasted our astronauts to the moon—350 feet tall—achieved a speed of
25,000 mi/h. That was an incredible feat.
 But 94,000 mi/h? A rocket that big wouldn’t even get off the ground!
Escape Velocity
Cont’d
• Consider a projectile of mass m, leaving the surface of a planet
(or some other astronomical body) with escape velocity v. It has
a kinetic energy k given by:
1 2
mv
2
Cont’d
• The projectile also has potential energy U given by:
2
GMm
11 m
U 
where G  6.67 10
is the gravitational constant
2
r
kg.s
and M is the mass of the planet.
Cont’d
• When the projectile reaches maximum height v=0
• Since v(instantaneous velocity) is the derivative of altitude
with respect to time. Therefore k = 0.

• Also as r the potential energy goes to zero. Based on the
principal of conservation of energy , the total energy of the
projectile at the planet’s surface must also have been zero.
Cont’d
1
2
K  U  mv  ( GMm
r )  0
2
This yields
v
2GM
r
Escape speed
Escape speed
• The escape speed does not depend on the direction in which
a projectile is fired.
• However, attaining the speed is easier if the projectile is
fired in the direction the launch site is moving as Earth
rotates about its axis.
How Escape Speeds are Calculated
•
The basic concept is based on the conservation of energy.
•
The KE of the satellite at launch equals the PE at the escape
point.
How Escape Speeds are Calculated
Solving for r:
How Escape Speeds are Calculated
Recall the the minimum speed for circular orbits is:
How Escape Speeds are Calculated
Recall the the minimum speed for circular orbits is:
Therefore:
Escape Compared to Orbital Speed
The End
….. Thank You …..