Download Lec14

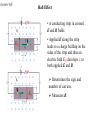
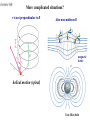
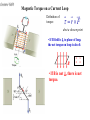
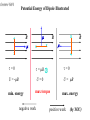
Lecture 14-1
Magnetic Field B
• Magnetic force acting on a moving charge q depends on q, v.
A
vB
(q>0)
F  qv  B
F  IL  B
If q<0
Lecture 14-2
Hall Effect
• A conducting strip in crossed
E and B fields
• Applied E along the strip
leads to a charge buildup on the
sides of the strip and thus an
electric field EH develops  to
both applied E and B.
EH
 Determines the sign and
number of carriers.
EH
 Measures B.
Lecture 14-3
Carrier Sign and Density from Hall Effect
Sign and density of charge carrier
is determined at equilibriumHall
voltage
 q E H   q vd  B  0
EH
EH EH d VH
vd 


B
Bd
Bd
and
J
I
n

vd q vd qA
EH
BId
BI
n 

VH qA VH q  A / d 
VH  B
for a given
current I and n
Lecture 14-4
Cyclotron
• "Magnetic Resonance Accelerator"
• "Dees" in constant magnetic field B
• Alternating voltage V is applied between the
Dees at the orbital frequency f:
v2
qvB  m
r
mv
r
 const.
qB
qB
2 r 2 m
qB
  2 f 
m
f 
v

• Particle will acquire an additional kinetic energy T
= qV each time it crosses the gap (ie twice per
revolution.. E=0 in Dees!).
mv
increases as v does
r
qB
problems  synchrotron
Lecture 14-5
Synchrotron
mv
r
qB
R is the same since B increases as v does
Lecture 14-6
More complicated situations?
v is not perpendicular to B
Also non-uniform B
magnetic
bottle
helical motion (spiral)
Van Allen belts
Lecture 14-7
Polar Light
High energy particles leaked out of the belt and interact with the
earth atmosphere.
Lecture 14-8
Warm-up
An electron (charge -e) comes horizontally into a
region of perpendicularly crossed, uniform E and B
fields as shown. In this region, it deflects upward
as shown. What can you do to change the path so
it remains horizontal through the region?
a)
b)
c)
d)
e)
Increase E
Increase B
Turn B off
Turn E off
Nothing
http://canu.ucalgary.ca/map/content/force/elcrmagn/simulate/magnetic/applet.html
http://canu.ucalgary.ca/map/content/force/elcrmagn/simulate/exb_thomson/applet.html
Lecture 14-9
Magnetic Force on a Current Loop
Force on closed loop current in uniform B?
– Force on top path cancels force on
bottom path (F = IBL)
– Force on right path cancels force
on left path. (F = IBL)
F  I LB
loop


 I  L  B
 loop 
0
closed loop
Uniform B exerts no net force
on closed current loop.
Lecture 14-10
Magnetic Torque on a Current Loop
Definition of
torque:
  rF
abut a chosen point
• If B field is  to plane of loop,
the net torque on loop is also 0.
B




• If B is not , there is net
torque.
Lecture 14-11
Calculation of Torque
• Suppose the coil has width b (the side
we see) and length a (into the screen).
The torque about the center is given by:
b
τ   r  F  2  sin   F
2
F  IaB
  Iab  B  sin 
 IA B sin 
area of loop
• Define magnetic dipole moment by
  IAn
  B
where n is normal to the
loop with RHR along I.
 
  p E

Lecture 14-12
Example of Magnetic Moment Calculation
A thin non-conducting disk of mass m
and uniform surface charge density 
rotates with angular velocity  as
shown. What is the magnetic moment?
n
mag. moment of the ring shown:
d    (r )(dr)  ( r )  n
2
dI
1
1
   R 2  R 2   QR 2 
4
4
1
L  I m   mR 2 
2
Q

L
2m

R

   d     r 3dr n
1
  R 4 
4
0
Lecture 14-13
Potential Energy of Dipole
• Work must be done to change the
orientation of a dipole (current loop)
in the presence of a magnetic field.
• Define a potential energy U (with
zero at position of max torque)
corresponding to this work.
θ
B
x
F

F
.

θ
U   τdθ

90
U   μB sin θdθ
90
Therefore,
U  μB cos θ 90  U   μB cos θ 
θ
U    B
Lecture 14-14
Potential Energy of Dipole Illustrated

B

x
B
B

x
x
=0
 = B X
=0
U = -B
U=0
U = B
min. energy
max torque
negative work
max. energy
positive work
(by YOU)
Lecture 14-15
PHYS241 - Quiz A
An electron (charge e) comes horizontally into a region of
perpendicularly crossed, uniform E and B fields as shown.
In this region, it is deflected upward as shown. What can
you do to change the path so it deflects downward instead
through the region?
a. Increase E
b. Turn B off
c. Decrease E
d. Slow down the electron
e. None of the above
Lecture 14-16
PHYS241 - Quiz B
A proton (charge +e) comes horizontally into a region of
perpendicularly crossed, uniform E and B fields as shown.
In this region, it goes straight without deflection. What can
you do to change the path so it deflects upward through the
region?
a. Increase E
b. Increase B
c. Turn B off
d. Slow down the proton
e. None of the above
Lecture 14-17
PHYS241 - Quiz C
A proton (charge +e) comes horizontally into a region of
perpendicularly crossed, uniform E and B fields as shown.
In this region, it deflects downward as shown. What can
you do to change the path so it remains horizontal through
the region?
a. Increase E
b. Turn B off
c. Turn E off
d. Slow down the electron
e. Increase B