* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download chapter 6
Introduction to general relativity wikipedia , lookup
Equivalence principle wikipedia , lookup
Coriolis force wikipedia , lookup
Lorentz force wikipedia , lookup
Lunar theory wikipedia , lookup
Schiehallion experiment wikipedia , lookup
Fictitious force wikipedia , lookup
N-body problem wikipedia , lookup
Roche limit wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Centrifugal force wikipedia , lookup
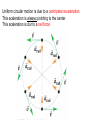
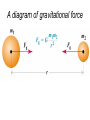
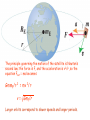
CHAPTER 6 CIRCULAR MOTION AND GRAVITATION Goals for Chapter 6 • To understand the dynamics of circular motion. • To study the unique application of circular motion as it applies to Newton’s Law of Gravitation. • To study the motion of objects in orbit as a special application of Newton’s Law of Gravitation. Uniform circular motion is due to a centripetal acceleration This aceleration is always pointing to the center This aceleration is dur to a net force • Period = the time for one revolution 1) Circular motion in horizontal plane: - flat curve - banked curve - rotating object 2) Circular motion in vertical plane Rounding a flat curve • The centripetal force coming only from tire friction. Rounding a banked curve • The centripetal force comes from friction and a component of force from the car’s mass A tetherball problem Dynamics of a Ferris Wheel HOMEWORK CH6 3; 5; 8; 13; 15; 19; 22; 29; 36; 40 • Each stride is taken as one in a series of arcs Spherically symmetric objects interact gravitationally as though all the mass of each were concentrated at its center A diagram of gravitational force Newton’s Law of Gravitation • Always attractive. • Directly proportional to the masses involved. • Inversely proportional to the square of the separation between the masses. • Masses must be large to bring Fg to a size even close to humanly perceptible forces. •Use Newton’s Law of Universal Gravitation with the specific masses and separation. Cavendish Balance •The slight attraction of the masses causes a nearly imperceptible rotation of the string supporting the masses connected to the mirror. •Use of the laser allows a point many meters away to move through measurable distances as the angle allows the initial and final positions to diverge. WEIGHT Gravitational force falls off quickly • If either m1 or m2 are small, the force decreases quickly enough for humans to notice. What happens when velocity rises? • Eventually, Fg balances and you have orbit. • When v is large enough, you achieve escape velocity. Satellite Motion The principle governing the motion of the satellite is Newton’s second law; the force is F, and the acceleration is v2/r, so the equation Fnet = ma becomes GmmE/r 2 = mv 2/r v = GmE/r Larger orbits correspond to slower speeds and longer periods. We want to place a satellite into circular orbit 300km above the earth surface. What speed, period and radial acceleration it must have? A 320 kg satellite experiences a gravitational force of 800 N. What is the radius of the of the satellite’s orbit? What is its altitude? F = GmEmS/r 2 r 2 = GmEmS/ F r 2 = (6.67 x 10 -11 N.m2/kg2) (5.98 x 10 24 kg) (320 kg ) / 800 N r 2 = 1.595 x 1014 m2 r = 1.26 x 107 m Altitude = 1.26 x 107 m – radius of the Earth Altitude = 1.26 x 107 m – 0.637 x 107 = 0.623 x 107 m