Download Transparancies for Energy & Momentum Section

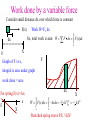
Handout II : Momentum &Energy
EE1 Particle Kinematics :
Newton’s Legacy
"I seem to have been only like a boy
playing on the seashore, and diverting
myself in now and then finding a
smoother pebble or a prettier shell than
ordinary, whilst the great ocean of truth
lay all undiscovered before me."
October 2004 http://ppewww.ph.gla.ac.uk/~parkes/teaching/PK/PK.html
Chris Parkes
Projectiles
Motion of a thrown / fired
object mass m under gravity
y
Velocity components:
v
vx=v cos 

x,y,t
x
a:
v=u+at:
x direction
ax=0
vx=vcos  + axt = vcos 
s=ut+0.5at2: x=(vcos )t
vy=v sin 
Force: -mg in y direction
acceleration: -g in y direction
y direction
ay=-g
vy=vsin  - gt
y= vtsin  -0.5gt2
This describes the motion, now we can use it to solve problems
Linear Momentum Conservation
• Define momentum p=mv
d p d (mv)
nd
• Newton’s 2 law actually F  dt  dt  m ddtv  ma
• So, with no external forces, momentum is
conserved.
• e.g. two body collision on frictionless
surface in 1D
before
m1
m2
0 ms-1
Initial momentum: m1 v0 = m1v1+ m2v2 : final momentum
after
v0
m1
m2
v2
v1
For 2D remember momentum is a VECTOR, must apply
conservation, separately for x and y velocity components
Energy Conservation
•Energy can neither be created nor destroyed
•Energy can be converted from one form to another
• Need to consider all possible forms of energy in a
system e.g:
–
–
–
–
–
Kinetic energy (1/2 mv2)
Potential energy (gravitational mgh, electrostatic)
Electromagnetic energy
Work done on the system
Heat (1st law of thermodynamics of Lord Kelvin)
• Friction  Heat
Energy measured in Joules [J]
Collision revisited
m1
v1
m2
• We identify two types of collisions
– Elastic: momentum and kinetic energy conserved
Initial k.e.: ½m1 v02 = ½ m1v12+ ½ m2v22 : final k.e.
– Inelastic: momentum is conserved, kinetic energy is not
• Kinetic energy is transformed into other forms of energy
See lecture example for cases of elastic solution
Newton’s cradle
1. m1>m2
2. m1<m2
3. m1=m2
v2
Efficiency
• Not all energy is used to do useful work
• e.g. Heat losses (random motion k.e. of molecules)
– Efficiency  = useful energy produced
×100%
total energy used
e.g. coal fired power station
Boiler
coal
Chemical energy
steam
40%
heat
Turbine
Generator electricity
Product of efficiencies at
each stage
Steam,mechanical work
Oil or gas, energy more direct : 70%
electricity
Work & Energy
Work is the change in energy that results from applying a force
• Work = Force F ×Distance s, units of Joules[J]
– More precisely W=F.x
– F,x Vectors so W=F x cos
• e.g. raise a 10kg weight 2m
• F=mg=10*9.8 N,
• W=Fx=98*2=196 Nm=196J
• The rate of doing work is the
Power
• Energy can be converted into work
– Electrical, chemical
– Or letting the weight fall
– (gravitational)
• Hydro-electric power station
mgh of
water
s
F

x
F
[Js-1Watts]
This stored energy has the potential to do work Potential
We are dealing with changes in energy
Energy
h
• choose an arbitrary 0, and look at  p.e.
0
This was gravitational p.e., another example :
Stored energy in a Spring
Do work on a spring to compress it or expand it
Hooke’s law
BUT, Force depends on extension x
Work done by a variable force
Work done by a variable force
Consider small distance dx over which force is constant
F(x)
Work W=Fx dx
X
dx
So, total work is sum W   F  dx   F ( x)dx
0
X
0
Graph of F vs x,
F
integral is area under graph
work done = area
For spring,F(x)=-kx:
x
F
X
dx
X
X
0
0
X
W   F ( x)dx    kxdx  [ 12 kx2 ]0X   12 kX 2
Stretched spring stores P.E. ½kX2