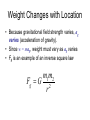* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Circular Motion and Gravitation
N-body problem wikipedia , lookup
Coriolis force wikipedia , lookup
Classical mechanics wikipedia , lookup
Jerk (physics) wikipedia , lookup
Seismometer wikipedia , lookup
Fictitious force wikipedia , lookup
Equations of motion wikipedia , lookup
Centrifugal force wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Mass versus weight wikipedia , lookup
Classical central-force problem wikipedia , lookup
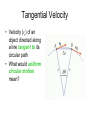
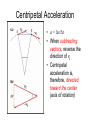
Circular Motion and Gravitation Holt Physics Chapter 7 Centripetal Acceleration • Circular motion: motion of an object that revolves about an axis of rotation Tangential Velocity • Velocity (vt) of an object directed along a line tangent to its circular path • What would uniform circular motion mean? vt depends upon radius • Object B must travel a greater distance to keep up with object A • SB > SA • But ΔtB = ΔtA • Therefore, vB > vA Centripetal Acceleration • Velocity is a vector (magnitude & direction) • Acceleration is a change in velocity • An object with constant speed, but changing direction, is accelerating • Acceleration of an object with uniform circular motion (constant vt) has centripetal acceleration Centripetal Acceleration • a = Δv/Δt • When subtracting vectors, reverse the direction of vi • Centripetal acceleration is, therefore, directed toward the center (axis of rotation) Centripetal Acceleration • Centripetal means “center seeking” and is always directed toward the center • Due to a change in direction of vt 2 vt ac r Centripetal Force Because Fc acts at right angles to the object’s circular motion, it changes the direction of the objects velocity Centripetal Force • Is the cause of centripetal acceleration • It is directed toward the axis of rotation • It is the net force acting on an object in uniform circular motion, i.e. it is the cause of circular motion • Newton’s second law applies • Fc=mac • Since ac = vt2/r • Fc=mvt2/r • Centrifugal force is a misunderstanding of inertia Newton’s Universal Law of Gravitation • Gravitational Force – Mutual force of attraction between particles of matter – Gravitational force is a very weak force – is proportional to the masses of the objects and inversely proportional to the square of the distance between their centers. Newton’s Universal Law of Gravitation m1m2 Fg G 2 r Fg is gravitational force G is constant of universal gravitation; G = 6.673 x 10-11N∙m2/kg2 (by Cavendish) m1 m2 are masses of the two bodies r is distance between centers of masses Newton’s Universal Law of Gravitation Newton’s Mountain Newton’s Thought Experiment A cannonball fired from sufficient height with sufficient velocity will orbit the earth. Objects in orbit are in continuous free fall They do not hit the earth because the earth curves away from the object • • http://spaceplace.nasa.gov/en/kids/orbits1.shtml http://galileoandeinstein.physics.virginia.edu/more_stuff/Applets/newt/ne wtmtn.html Gravitational Field • Gravity is a field force • Gravitational Field • Field strength varies with distance from Earth’s center • Is described by g, – i.e. the value of g describes the strength of the gravitational field at a particular location in the field Weight Changes with Location • Because gravitational field strength varies, ag varies (acceleration of gravity). • Since w = mag, weight must vary as ag varies • Fg is an example of an inverse square law m1m2 Fg G 2 r 7.3 Motion in Space Astronomer Ptolomey Planets orbit… Earth Type of orbit Epicycles Copernicus Sun Circular Kepler Sun Elliptical Kepler’s Laws of Planetary Motion 1. The Law of Orbits: All planets move in elliptical orbits, with the sun at one focus. 2. The Law of Areas: A line that connects a planet to the sun sweeps out equal areas in equal times. 3. The Law of Periods: The square of the period of any planet is proportional to the cube of the average distance from the sun, T r 2 3 Kepler’s Second Law The Law of Areas: A line that connects a planet to the sun sweeps out equal areas in equal times Kepler's Law Simulation Kepler’s 3rd Law Describes Orbital Period Period and speed of an object in Circular O rbit Orbital Period Orbital speed r3 m T 2 vt G Gm r whe re m is the mass of the orbited mass Weight & Weightlessness • A bathroom scale reads the normal force of the scale acting on your feet • Under normal conditions this equals your weight • Suppose you stand on a scale… • If someone were to push down on your shoulders, how would the normal force change? • What if someone lifted you up somewhat? • What if the scale was in an elevator? • What happens when the elevator begins to go up? • What happens when it begins to go down? • What would the scale read if the elevator was in free fall? • • • • In these situations, did your mass change? Did the scale readings change? So, did your true weight change? What did change was your apparent weight Apparent Weight Torque • a quantity that measures the ability of a force to rotate an object about an axis • is not a force • “turning ability” • the product of force and “lever arm” • τ = F · d sinθ • Lever arm (d) is distance perpendicular to direction of force to axis of rotation Fd sin Torque • Sign (+) is counterclockwise (-) is clockwise • Net Torque when 2 or more forces act to rotate the same object, τnet = Στ τnet = τ1 + τ2 = F1d1 + F2d2 Torque Equilibrium • Sum of torques = 0 • ∑τ = 0; τ clockwise = τcounterclockwise • An object is in “balance” like a teetertotter Mobiles • Are applications of torque equilibrium Simple Machines • All machines are combinations of simple machines • Purpose is to change magnitude or direction of an input force • Mechanical Advantage describes the ratio of output and input forces Fout MA Fin Ideal vs. Actual Mechanical Advantage • Ideal MA MA if there were no friction d = lever arm d in IMA d out • Actual MA MA that takes friction into account Fout AMA Fin Machines and Work • Machines do not change the amount of work • Machines make work easier Efficiency • A measure of how well a machine works Wout eff Win • A less efficient machine produces less output per input • A less efficient machine requires more input to get the same output Six Simple Machines • • • • • • Lever Inclined Plane Wheel & axle Pulley Wedge Screw