Download Oscillations

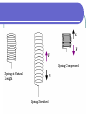
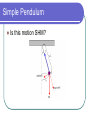
Oscillations - SHM
Oscillations

In general an
oscillation is simply
aback and forth
motion
 Since the motion
repeats itself, it is
called periodic
 We will look at a
special type of
oscillation - SHM
Simple Harmonic Motion

SHM is a result of the restoring force
varying linearly with the displacement.

In other words if you double the distance
moved by the oscillator, there will be
twice as much force trying to return it to
its natural state
SHM

A mass on a spring is the prime example
of SHM since the force that restores it to
its equilibrium position is directly
proportional to the amount by which the
spring is stretched.
Hook’s Law

The law that governs how spring stretches
F = -kx



F – force exerted by the spring (N)
x – the amount by which he string is stretched or
compressed (m)
k – spring constant. A measure of how “stiff” the
spring is (N/m)
A small spring has a k= 200 N/m
the neg. sign indicate that displacement and
force is in opposite direction
Mass Oscillating on a Spring
(1)
(3)
(2)
(4)
(5)
(6)
(7)
New formula
Since acceleration is not constant our
Big 4 Equations do not work
 F = ma is still ok but a is always
changing
 Calculating period:

T does not depend on amplitude – does this make
sense?

Frequency:
SHM - Example

Many skyscrapers use huge oscillating blocks of concrete to help
reduce the oscillation of the building itself. In one such building
the 3.73x105 kg block completes one oscillation in 6.80 s. What is
the spring constant for this block?
Additional Problems

A block of mass 1.5 kg is attached to the end of a vertical spring of force
constant k=300 N/m. After the block comes to rest, it is pulled down a
distance of 2.0 cm and released.
(a) What is the frequency of the resulting oscillations?
(b) What are the maximum and minimum amounts of stretch of the
spring during the oscillations of the block?

When a family of four people with a mass of 200 kg step into their 1200
kg car, the car's springs compress 3 cm.
(a) What is the spring constant of the car's springs, assuming they act as
a single spring?
(b) What are the period and frequency of the car after hitting a bump?

A small insect of mass 0.30 g is caught in a spiderweb of negligible
mass. The web vibrates with a frequency of 15 Hz.
(a) Estimate the value of the spring constant for the web.
(b) At what frequency would you expect the web to vibrate if an insect of
mass 0.10 g were trapped?
Energy Involved with SHM

Let’s look at a similar situation but
concentrate on the energy of the object

Energy stored in a spring (potential
energy)

U =PE = ½ kx2
Energy of SHM
1
3
2
4
Energy Formula

If total energy = PE + KE
½ kx2 + ½ mv2

Then Total energy =PE (max) (KE = 0)
= ½ kx2max
Remember X(max) = Amplitude
Velocity

If we combine all our formulas:

Which is useful when we solve for v
Simple Pendulum

Is this motion SHM?
Pendulums

Weight is broken into components


Y component = tension of rope
X component = restoring force ( brings the
pendulum back resting position)


F = -mg(sinθ) (neg. because it acts opp to displacement)
If the angle is small and measured in radians
the sin of angle basically equals the angle
itself (only if θ < 15°)

Therefore F=-mgθ

Now the arc length “x” is given by


Which means that we can replace the angle In
the force formula with x/L



X=Lθ
F = -mg (x/L)
F = (mg/L)x
The formulas is just F = -kx with the mg/L
taking the place of k
 Therefore we do have SHM
Period of a Pendulum

Period of a Spring
Replace the k with mg/L
 Period of a pendulum

