* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Fluid Flow
Hemorheology wikipedia , lookup
Lattice Boltzmann methods wikipedia , lookup
Airy wave theory wikipedia , lookup
Hydraulic machinery wikipedia , lookup
Wind-turbine aerodynamics wikipedia , lookup
Aerodynamics wikipedia , lookup
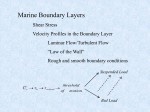
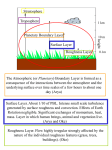
Boundary layer wikipedia , lookup
Fluid thread breakup wikipedia , lookup
Reynolds number wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Accretion disk wikipedia , lookup
Bernoulli's principle wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Fluid Flow Pressure, momentum flux and viscosity. How can we attack this problem? (1) Define viscosity Viscosity-fluid property that influences the rate of fluid flow under stress. y The viscosity is the ratio between the shear stress and the velocity gradient between the plates, or dv( x) dy Newton’s Law of Viscosity Units of viscosity d v x dy Pa m s m Pa s Layers of fluid particles with top layer moving faster than bottom layer Activation energy energy Position o exp log log activation_energy log o RT activation_energy 1 R T log o activation_energy 1 T R The top plate drags the fluid particles in the top fluid layer, which then drag the particles in the adjacent lower layer, which then drag the particles in the next lowest layer, and so on—thus giving rise to momentum transfer Momentum transfer Units on shear stress and pressure Force/area=mass*length/time2 * 1/area =mass * length/time * 1/time * 1/area = mass*velocity * 1/(time * area) = momentum/(time*area) = momentum flux A momentum flux (or stress) multiplied by a cross sectional area is a FORCE! Forces balance at steady state (equilibrium) Rate of momentum in =rate of momentum out at steady state. 2. Determine velocity profile. If flow is fully developed, the fluid velocity only depends on y. V(x) yx d v( x) dy 0 y y y y ‘control volume’ z x Patm y x x x High Pressure Papplied Low Pressure Hydrostatic pressure varies with x while shear stress varies with y! We only have to consider the shear stress acting normal to the xz plane and the hydrostatic pressure component acting normal to the yz plane. yx yx xz P x - Px xyz y y y 0 yx yx xz P x - Px xyz y y y yx yx P x- P y y x x y y x d d P yx d y dx 0 0 Function of x unless P=constant or P linear with x. Velocity can only depend on y d yx dy P L d dy d y yx P L dy yx P L C is the integration constant from indefinite integration y C If the velocity is a local maximum at y=0 (center in between plates), then C=0 yx d v( x) dy P L d v ( x) d y dy y v ( x) C1 v ( x) P 2L 2 y C1 P 2L P 2L 2 2 y2 P L y dy