Download Document

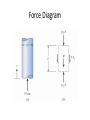
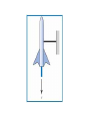
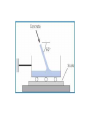
Fluid Mechanics 10
Control Volume Approach
Intensive and Extensive Properties:Extensive Properties depends on mass like
mass, m, momentum, mv and energy, E.
The intensive properties does not depend on
mass, The intensive property for momentum
is velocity v, and for energy is e, weight is g
Reynolds Transport Theorem
Take B is general extensive property and b is the
intensive one for it
At t time B(t)=Bcv(t)+∆Bsc(t)
At t+∆t B(t+∆t)=Bcv(t+∆t)+∆Bsc(t+∆t)
Change in B for ∆t
B(t+∆t)−B(t) Bcv(t+∆t)−Bcv(t)
=
+
∆𝑡
∆𝑡
∆Bsc(t+∆t)−∆Bsc(t)
∆𝑡
For ∆t ≈ 0
𝑑𝐵
B(t+∆t)−B(t)
= lim∆𝑡
𝑑𝐵𝑐𝑣
𝑑𝑡
𝑑𝐵𝑐𝑠
𝑑𝑡
Bcv(t+∆t)−Bcv(t)
= lim∆𝑡
∆𝑡
→0
∆Bcs(t+∆t)−∆Bcs(t)
= lim∆𝑡
∆𝑡
→0
So
𝑑𝐵 𝑑𝐵𝑐𝑣 𝑑𝐵𝑠𝑐
=
+
𝑑𝑡 𝑑𝑡
𝑑𝑡
Take B=m*b where B is extensive and b is intensive
𝑑𝐵
= ρ ∗ 𝑏 ∗ 𝑑𝑉 + 𝑐𝑠 𝑚ʹ𝑜 ∗ 𝑏𝑜 − 𝑐𝑠 𝑚ʹ𝑖 ∗ 𝑏𝑖
𝑑𝑡
For steady flow
𝑑𝐵
= 𝑐𝑠 𝑚ʹ𝑜 ∗ 𝑏𝑜 − 𝑐𝑠 𝑚ʹ𝑖 ∗ 𝑏𝑖
𝑑𝑡
Newton's Laws
First Law:- An object remains at rest or at a
constant velocity unless force acted upon it
Second Law:- F=m*a
Third Law:- When one body creates a force on a
second body, the second body creates a force
equal in magnitude and opposite in direction to
the first body.
Force Diagram
Momentum
The Momentum is the product of the mass
and velocity of an object.
Pm=F*v where pm is the momentum
Momentum units is Kg*m/s
𝑑𝑝𝑚
=𝐹
𝑑𝑡
Momentum equation
General Equation
𝐹= ρ ∗ 𝑣 ∗ 𝑑𝑉 +
𝑐𝑠 𝑚ʹ𝑜
∗ 𝑣𝑜 −
For steady flow
𝐹=
𝑐𝑠 𝑚ʹ𝑜
∗ 𝑣𝑜 −
𝑐𝑠 𝑚ʹ𝑖
∗ 𝑣𝑖
𝑐𝑠 𝑚ʹ𝑖
∗ 𝑣𝑖
Example
The sketch below shows a 40 g rocket, of the type
used for model rocketry, being fired on a test stand
in order to evaluate thrust. The exhaust jet from
the rocket motor has a diameter of d = 1 cm, a
speed of ν = 450 m/s, and a density of ρ = 0.5
kg/m3. Assume the pressure in the exhaust jet
equals ambient pressure, and neglect any
momentum changes inside the rocket motor. Find
the force Fb acting on the beam that supports the
rocket.
Solution
1- Select the control
volume.
2- Draw the force
diagram.
3- Draw the moment
diagram.
4- Write the equation
calculate the missing
𝐹= ρ ∗ 𝑣 ∗ 𝑑𝑉 +
𝑐𝑠 𝑚ʹ𝑜
∗ 𝑣𝑜 −
𝑐𝑠 𝑚ʹ𝑖
∗ 𝑣𝑖
neglect any momentum changes inside the rocket
Vi=0.0
𝐹=
𝑐𝑠 𝑚ʹ𝑜
∗ 𝑣𝑜
−𝐹𝑏 − 𝑚 ∗ 𝑔 = −𝑚ʹ ∗ 𝑣𝑜
Where m=0.4 kg, mʹ=ρ*A*v, d=0.01m, v=450m/s
𝐹𝑏 = 𝑚ʹ ∗ 𝑣𝑜 − 𝑚 ∗ 𝑔
0.012
=(Π*
*4502
4
∗ 0.5) − (0.4 ∗ 9.81) = 7.56𝑁
Example
As shown in the sketch, concrete flows into a cart
sitting on a scale. The stream of concrete has a
density of ρ = 150 ibm/ft3, an area of A = 1 ft2,
and a speed of V = 10 ft/s. At the instant shown,
the weight of the cart plus the concrete is 800 lbf.
Determine the tension in the cable and the
weight recorded by the scale. Assume steady
flow.
Solution
The problem has two direction x, z we will
apply the equation into the 2-D according
to θ
𝐹= ρ ∗ 𝑣 ∗ 𝑑𝑉 + 𝑐𝑠 𝑚ʹ𝑜 ∗ 𝑣𝑜 − 𝑐𝑠 𝑚ʹ𝑖 ∗ 𝑣𝑖
Where the flow is steady , no out velocity
𝐹=− 𝑐𝑠 𝑚ʹ𝑖 ∗ 𝑣𝑖
Direction X
𝐹𝑥=− 𝑐𝑠 𝑚ʹ𝑖 ∗ 𝑣𝑖x
−𝑇 = −ρ ∗ 𝐴 ∗ 𝑣 2 ∗ cos(60) = −150 ∗ 1 2
∗ 102 ∗ cos(60)
T = 233 lbf
Direction z
𝐹𝑧=− 𝑐𝑠 𝑚ʹ𝑖 ∗ 𝑣𝑖 z
𝑁 − 𝑊 = −ρ ∗ 𝐴 ∗ 𝑣 2 ∗ −sin(60) = −150
∗ 1 2 ∗ 102 ∗ sin 60 = 403𝑙𝑏𝑓
N = 1200 lbf