Download Statics - Chabotcollege.edu

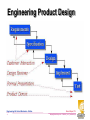
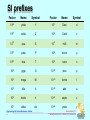
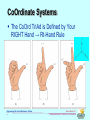
Engineering 36
Chp 1
Introduction
Bruce Mayer, PE
Licensed Electrical & Mechanical Engineer
[email protected]
Engineering-36: Vector Mechanics - Statics
1
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Learning Statics
 There is ONLY ONE WAY to Learn
Statics
Work LOTS of Problems
• Work Thru, and UNDERSTAND, all
Sample Problems
• Work Chp Problems for Which the Book
Provides Answers
– Handily Located in the Back of the Book; See
“ANSWERS TO SELECTED PROBLEMS”
Engineering-36: Vector Mechanics - Statics
2
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Class Structure – ENGR36
 Lecture TTh 1:00-1:50p
• PowerPoint Instruction-Presentation on The
Interactions of Forces (Push/Pull) and
Moments (Twists) on NONmoving structures
 Lab – TTh 2:00-3:15p
• Tu: WhiteBoard Example Solutions to
Problems Similar to the LPS (HomeWork)
Problems
• Th: Work in Computer Lab 3906A on the
Mastering Engineering LPS Problems
Engineering-36: Vector Mechanics - Statics
3
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
If you can’t Make the Lab Every
time... Don’t Worry
 I will post my solved Examples on the
ENGR36 Course WebPage
 Any Student can Work at his/her own
Time & Location in place of the lab AS
LONG AS the LPS are Submitted to
Mastering Engineering ON TIME
 If a student can not make the Lab
Session, I suggest forming an ENGR36
study Group outside of class times
Engineering-36: Vector Mechanics - Statics
4
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Mastering Engineering
http://www.masteringengineering.com/
Engineering-36: Vector Mechanics - Statics
5
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Mastering Engineering
http://www.masteringengineering.com/site/register/new-students.html
Pick One, then Continue
Engineering-36: Vector Mechanics - Statics
6
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Mastering Engineering: $60.50
http://www.mypearsonstore.com/bookstore/product.asp?isbn=0132915545&xid=PSED
 An Access Code is provided with the
TextBook Available in the BookStore
 Students who purchased the book from
another source can purchase Stand-Alone
Mastering Engineering for $60.50
Engineering-36: Vector Mechanics - Statics
7
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
If you received a Course ID
from your instructor, click Yes,
enter your Course ID and click
Continue.
CHABOTENGR36FA12
Engineering-36: Vector Mechanics - Statics
8
If you DO NOT have a Course
ID, follow the instructions on
the NEXT slide.
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
W12345678
Your instructor may provide specific
instructions for completing this field.
If so, enter the appropriate
information and click Continue.
Use “W” Number
as Student ID
Engineering-36: Vector Mechanics - Statics
9
If you are not sure what to enter,
contact your instructor or click Skip
This Step.
(You can enter your Student ID later.)
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Registering Tips Video
 http://www.masteringsupport.com/video
s/registration_tips/registration_tips.html
Engineering-36: Vector Mechanics - Statics
10
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Engineering Product Design
Engineering-36: Vector Mechanics - Statics
11
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Engineering Product Design
 Requirements/Goals
• The goal of this
phase is to figure out
exactly what the
customer wants
 Specification
• describe exactly
what the product will
do and how it will
perform
Engineering-36: Vector Mechanics - Statics
12
• focus on WHAT the
product is supposed
to do, not HOW it is
supposed to do it
 Design
• Conceptual →
Generate Broad
Concept Solutions
• Preliminary →
Choose 2-3
Concepts for Testing
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Engineering Product Design
 Design
• Detailed → Select
“winning” solution
• Sweat details →
select materials,
Perform engineering
analyses, make
Engineering DWGs,
determine production
and test methods
 Implement
• Make a PHYSICAL
Prototype unit
Engineering-36: Vector Mechanics - Statics
13
 Test
• Test every item in
the performance
specification →
Possible OutComes
– The product does
NOT meet the spec
– The product meets the
spec but the spec was
WRONG
– customer CHANGED
his/her mind
– product MEETS the
spec and customer
is HAPPY
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Engineering Analysis
 Goal
• What EXACTLY do we want to determine?
– Suggest including the UNITS for the “answer”
 Given
• Summarize KNOWN conditions and
previously collected DATA
 Assume (this HAS to be done)
• Make an analytical MODEL
• List Important assumptions
Engineering-36: Vector Mechanics - Statics
14
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Assumption Digression
 BMayer 2001 JVST Paper
• See
ENGR45
for More
Details
Engineering-36: Vector Mechanics - Statics
15
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Assumption Digression
 PARTIAL
Assumption List
• 100% Vapor
Saturation at Bubble
Edge
• Gases in bubble
behave as perfect
gases
• Bubbles are
Spherical
– Radial Symmetry
Engineering-36: Vector Mechanics - Statics
16
• Diffusion Coefficient
is Constant
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Engineering Analysis
 Draw Diagram if Possible
• Sketching a Diagram is critical
• Take time to make a Sketch that is Clear
and in Proportion (roughly to scale)
 Create Math Model
• Make equations based on known scientific
(physics, chem) or engineering principles
 Solve Math Model
• Math Processors (MATLAB, Excel) helpful
Engineering-36: Vector Mechanics - Statics
17
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Engineering Analysis
 Check Results
• Make a “Reality
Check” on Results
• Test with KNOWN
inputs and compare
to the KNOWN result
• Test with a WIDE
range of inputs to test
“robustness”
Engineering-36: Vector Mechanics - Statics
18
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Mechanics – General
 Mechanics  The Physical Science Which
Describes Or Predicts The Conditions Of
REST Or MOTION For BODIES Under The
Action Of FORCES and/or MOMENTS
• Some Classes of Mechanics Analysis
– Rigid Bodies
 Statics → NO Motion
 Dynamics → Moving in General
– Deformable Bodies → Forces Interact with MATERIAL
Properties
 3rd yr course at the University Level
– Fluid Mechanics → almost always deforming materials
 Compressible → gas
 Incompressible → liquids
Engineering-36: Vector Mechanics - Statics
19
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Rigid Body – Special Case
 Rigid-Body Analysis Considers All Bodies To
Be Perfectly Stiff → NO Deformation
• Not Strictly True In Practical Situations as All
Physical Structures Deform (However Slightly)
When Subjected to Force-Loading.
– Rigid Body Analysis Applies When Deformations Are
“Small” and so Do Not “Significantly” Affect The
Conditions Of Equilibrium Or Motion
 i.e., Can Neglect Deformation For Equil/Motion Analysis
 Rigid Body ≡ A Body is Considered Rigid
When The Relative Movement Between Its
Parts is Negligible
Engineering-36: Vector Mechanics - Statics
20
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Statics – Further Special Case
 Statics Is A SubClass of Rigid Body
Mechanics Analysis
 Statics ≡ Study Of Equilibria Of A System
Without Regard To Inertia Forces Or Velocity
Dependent Forces → No or Const. Motion
• Apply Newton’s 2nd Law Using Vector Notation
 F  ma
but a  0 
 F  0!
• Consequences of Static Rigid-Body Conditions
– System Accelerations Are ZERO
– Force InterActs with CONFIGURATION Only
– governing equations are ALGEBRAIC In Nature
Engineering-36: Vector Mechanics - Statics
21
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Statics - Fundamental Concepts

Static Analysis is Based on Incompletely
Defined, But Thoroughly Familiar Concepts
1. SPACE ≈ The Geometric Region Occupied By
Bodies Whose Positions Are Described By
Linear and Angular Measurements
Cartesian
Relative to a Coordinate System
Space
2. TIME ≈ The Measure Of The
Succession Of Events
3. MASS ≈ The Measure of the Body’s Inertia,
Which Is Its Resistance to a Change Of Motion.
Sometimes Called "Quantity Of Matter“
4. FORCE ≈ The Action Of One Body On Another
Engineering-36: Vector Mechanics - Statics
22
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Newtonian Mechanics

Sir Isaac Newton (1642-1727) Was the First
Person To Mathematically Describe the
Physical Relationship Between the
Fundamentals
•

In Newtonian Mechanics Space, Time, And Mass
Are Absolute, And Independent Of Each Other
Newton’s Laws
1. Objects At Rest Will Stay At Rest, and
Objects In Motion Will Stay In Motion In A
Straight Line Unless Acted Upon By An
Unbalanced Force (Resultant Force = 0).
Engineering-36: Vector Mechanics - Statics
23
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Newtonian Mechanics cont.
2. Force Is Equal To Body
Mass Times its
Acceleration; Mathematically
 F  ma

Note: for STATIC; i.e.,
NonMoving, systems a = 0
3. For Every Action There
Is Always An Opposite
And Equal Reaction that
is CoLinear
Engineering-36: Vector Mechanics - Statics
24
Sir Issac Newton
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Systems of Units
 Base units For Static Analysis
System
SI Units
US Customary Units
Length
Mass
Time
Meter (m)
Kilogram (kg)
Second (s)
Foot (ft)
Slug (slug)
Second (s)
 FORCE is the Most Important Derived Unit
• Find the SI Consistent Force Unit by Applying a
Unitary Acceleration, a, of 1 m/s2
– Funit = (1 kg)•(1 m/s2) = 1 N (newton)
• Recall for a Weight, the Acceleration is g.
One kg “weighs”:
– W = mg = (1 kg)•(9.81 m/s2) = 9.81 N
Engineering-36: Vector Mechanics - Statics
25
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Tips on Units
 Maintain Units Through ALL Calculations
• Serves as A Consistency Check
 Use SI Prefixes (Next Slide) to Avoid
Scientific Notation
• But for Complex Calculations, Convert back to
Non-Prefixed SI Units to Avoid Order-of
Magnitude Errors
 Separate 3-Digit Groups with a Space,
NOT a Comma
• YES → 45 611 m
Engineering-36: Vector Mechanics - Statics
26
NO → 789,321 s
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
SI prefixes
Factor
Name
Symbol
Factor
Name
Symbol
1024
yotta
Y
10-1
Deci
d
1021
zetta
Z
10-2
Centi
c
1018
exa
E
10-3
milli
m
1015
peta
P
10-6
micro
µ
1012
tera
T
10-9
nano
n
109
giga
G
10-12
pico
p
106
mega
M
10-15
femto
f
103
kilo
k
10-18
atto
a
102
hecto
h
10-21
zepto
z
101
deka
da
10-24
yocto
y
Engineering-36: Vector Mechanics - Statics
27
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
US Units  lbs vs. slugs
 In The US Customary System the Unit of
FORCE  Pound (lb)
• F = ma
and
1 lb = m•(1 ft/s2)
• Thus m = 1 lb•s2/ft = 1 slug
 Weight of 1 slug by gravity?
• W = mg
Where
g = 32.2 ft/s2
• Thus Wslug = 32.2 slug•ft/s2 = 32.2 lb
 Summary
• 1 lb Is The Force Required To Give A Mass Of 1
Slug An Acceleration Of 1 ft/s²
• 1 lb Is The Force Required To Give A Mass Of
1/32.2 Slug An Acceleration Of 32.2 ft/s²
Engineering-36: Vector Mechanics - Statics
28
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Unit Conversion
 As Noted Before Unit-Consistency Is Critical
for Arriving at a Proper Answer
 To Convert From One Set of Units to Another
use the “Cross-Out” Division Method
• e.g. Given a Speed, , of 60 mph; find ft/s & m/s
– Given From ref Bk: 1mi = 5280ft
and 1m = 3.281ft


 fps   60
 SI
1hr = 3600s
mi   5280 ft   1hr 
ft



88
 
 

hr   mi   3600s 
s
m
 ft   1m 
  26.82
  88   
s
 s   3.281 ft 
Engineering-36: Vector Mechanics - Statics
29
and
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Numerical Precision
 Precision is Determined by The PHYSICAL
Situation, NOT the CALCULATOR
• In Particular, A Computed Result Can be NO MORE
Precise Than The LEAST Accurate of
– Physically Measured (or Derived from Measured) DATA
– The Precision of the Calculation
 This Was Issue in the SlideRule Days, But Rarely Now
• Example: Find the Average of this Physically Reliable
Data Set (13.47, 9.9, 7.803)
avg 
13.47  9.9  7.803
 10.391 (by calc)
3
 10.4 (reliably)
– In This Example, the Middle Value Governs Precision
Engineering-36: Vector Mechanics - Statics
30
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Numerical Precision, cont.
 It is Physically difficult to Make Precise and
Reliably-Accurate Measurements to Better
Than 1 part per 1 000 (1 ppt); or about 0.1%
• Most Practicing Engineers are Very Skeptical of
Any Data/Calculations Presented at
1 part in 10 000 (or more)
 Good “Rule of Thumb”
• 4 Figures For Values Starting With No. 1
– Called “3½” Significant Figures
• 3 Figures In All Other Cases
Engineering-36: Vector Mechanics - Statics
31
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
CoOrdinate Systems
 The CoOrd TriAd is Defined by Your
RIGHT Hand → Rt-Hand Rule
Engineering-36: Vector Mechanics - Statics
32
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Right-Hand Rule
 Thumb points in the positive x direction
 Index finger points in
the positive y direction
 Middle finger points in
the positive z direction
 Used to define positive rotation
• Point thumb in the positive direction along
the axis which is perpendicular to the plane
of rotation
• The fingers point in the direction of
positive rotation
Engineering-36: Vector Mechanics - Statics
33
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Vectors
 VECTOR ≡ Parameter Possessing Magnitude
And Direction, Which Add According
To The Parallelogram Law
• Examples: Displacements,
Velocities, Accelerations, FORCES
 SCALAR ≡ Parameter Possessing
Magnitude But Not Direction
• Examples: Mass, Volume, Temperature
 Vector Classifications
• FIXED Or BOUND Vectors Have Well Defined
Points Of Application That CanNOT Be Changed
Without Affecting An Analysis
Engineering-36: Vector Mechanics - Statics
34
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Vectors cont.
• FREE Vectors May Be Moved In Space Without
Changing Their Effect On An Analysis
• SLIDING Vectors May Be Applied Anywhere Along
Their Line Of Action Without Affecting the Analysis
• EQUAL Vectors Have The Same Magnitude And
Direction
• NEGATIVE Vector Of a Given Vector Has The
Same Magnitude but The Opposite Direction
Equal Vectors
Negative Vectors
Engineering-36: Vector Mechanics - Statics
35
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Vector Representations
 MagAngle
 Unit Vectors
• Length of “Unit”
Vectors (i, j, k) = 1
• Magnitude ≡ ||V||
= Geometric Length
• Space Angles:
θx, θy, θz
Engineering-36: Vector Mechanics - Statics
36
 More on Vector
“DeComposition” in
future lectures
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Engineering Drawings
 Formal Drawing
 Informal Drawing
• Contains all
information needed
for FABRICATION or
ASSEMBLY
Engineering-36: Vector Mechanics - Statics
37
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Free-Body Diagrams
 SPACE DIAGRAM 
A Sketch Showing
The Physical
Conditions Of The
Problem
Engineering-36: Vector Mechanics - Statics
38
 FREE-BODY
DIAGRAM  A
Sketch Showing
ONLY The Forces
Acting On The
Selected Body
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Suggested Review → Trig
 Solving Statics Problems Often Involves
Non-Right Triangle Geometry. Some Useful
Relationships (See your Math Book)
 Law of Sines
 Law of Cosines
 a=13, c=17, B=43°
 a=11, b=19, C=101°
• A=31.4°, C=105.6°
b=24
Engineering-36: Vector Mechanics - Statics
39
• c = 23.7
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Battle of the TriAngle
 If 3 SIDE-LENGHTS are
known → Use Cos-Law to
Find any angle
• Solve Eqn at Right for cos(c)
 If 2 SIDE-LENGTHS and the
Included Angle are known
→ Use Cos-Law to find the Opp Side-Length
 Use Sin-Law for
• 2-ANGLES & 1-SIDE known
• 2-SIDES & NonIncluded Angle
Engineering-36: Vector Mechanics - Statics
40
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Done for 1st Meeting
 Please see
me if you
would like to
ADD
Static Loading
Engineering-36: Vector Mechanics - Statics
41
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Engineering 36
Appendix
Bruce Mayer, PE
Registered Electrical & Mechanical Engineer
[email protected]
Engineering-36: Vector Mechanics - Statics
42
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Newtonian Mechanics cont.
2. Force Is Equal To Body Mass Times its
Acceleration; Mathematically
 F  ma
3. For Every Action There Is Always An Opposite
And Equal Reaction

Newton’s Law of Gravitation
GMm
F 2
( F a SCALAR)
r
M
F
 F  mutual force of attraction between 2 particles
 G  universal constant known as the
constant of gravitation
 M, m  masses of the 2 particles
 r  distance between the 2 particles
Engineering-36: Vector Mechanics - Statics
43
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
-F
m
Weight
 Consider An Object of mass, m, at Height, h,
Above the Surface of the Earth, Which as
Radius R
• Then the Force on the Object (e.g., Yourself)
GMm
F
R  h 2
GM
but R  h  F  m 2  mg
R
 This Force Exerted by the Earth is called Weight
• While g Varies Somewhat With the Elevation &
Location, to a Very Good Approximation
– g  9.81 m/s2  32.2 ft/s2
Engineering-36: Vector Mechanics - Statics
44
W  mg
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt
Earth Facts
 D  7 926 miles (12 756 km)
 M  5.98 x 1024 kg
• About 2x1015 Empire
State Buildings
 Density,   5 520 kg/m3
• water  1 027 kg/m3
• steel  8 000 kg/m3
• glass  5 300 kg/m3
Engineering-36: Vector Mechanics - Statics
45
Bruce Mayer, PE
[email protected] • ENGR-36_Lec-01_Introduction.ppt