Download ppt - Wits Structural Chemistry

Ligand Substitution Reactions:
Rates and Mechanisms
Stoichiometric and Intimate Mechanisms
• We can think of a reaction mechanism at two different levels.
– The reaction may occur through a series of distinct steps
each of which can be written as a chemical equation.
» This series of steps is a stoichiometric mechanism.
– We can also consider what is happening during each of
these individual steps.
» These details constitute the intimate mechanism of the
reaction.
Stoichiometric Mechanism
• Each step in the stoichiometric mechanism has a rate or
equilibrium constant associated with it.
• The stoichiometric mechanism looks at the reactants,
products and intermediates that are involved in a reaction.
• Each species considered exists in potential minimum along
the reaction coordinate.
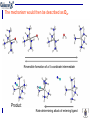
Stoichiometric mechanism: the sequence of elementary steps in a reaction
X
L
Y
L
-x
L
M
L
L
L
L
+Y
L
M
L
L
M
L
L
L
L
L
5 coordinate intermediate
Dissociative Mechanism, D
X
L
X
L
+Y
L
M
L
L
-x
L
M
L
L
Y
Y
L
L
M
L
L
L
L
L
7 coordinate intermediate
Associative Mechanism, A
In general, a D mechanism requires evidence for the
existence (structural, spectroscopic) of an intermediate with
reduced coordination number. An A mechanism requires
evidence of an intermediate with increased coordination
number.
If there is no identifiable intermediate, then we have to
assume an interchange mechanism is operating
X
X
L
L
+Y
L
M
L
Y
L
-x
L
M
L
L
=|
Y
L
L
L
L
M
L
L
L
transition state rather than an intermediate
Interchange Mechanism, I
Intimate mechanism: this describes the nature of the
process in the rate-determining step.
If the rate is strongly dependent on the nature of the entering group, then
the intimate mechanism is associative. We say the reaction is under
associate activation. The symbol is a subscript a.
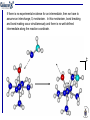
Suppose for the reaction
[M(NH3)3(OH2)]n+ + Lm− → [M(NH3)3L](n-m)+ + H2O
1) there is spectroscopic evidence for the existence of a 5
coordinate intermediate;
2) the rate of the reaction is strongly dependent on the nature
of L (for example, if L = H2O the reaction occurs 4 orders of
magnitude slower than if L = CN−)
(1) tells us that we are dealing with an A stoichiometric mechanism
(2) tells us that the intimate mechanism is a
The mechanism of the reaction is Aa
rate determining step
intermediate
rate determining process
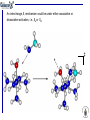
Whilst less common the situation could arise where the reaction proceeds
through an intermediate of reduced coordination number (D) and this is
followed by rate-determining attach of entering L on the intermediate (a).
The mechanism would then be described as Da.
The mechanism would then be described as Da.
Reversible formation of a 5 coordinate intermediate
Product
Rate-determining attack of entering ligand
rate determining step
In a Ad reaction, formation of the intermediate of higher coordination
number occurs relatively rapidly; the rate-determining step is the
dissociation of a ligand from the intermediate
If there is no experimental evidence for an intermediate, then we have to
assume an interchange, I, mechanism. In this mechanism, bond breaking
and bond making occur simultaneously and there is no well-defined
intermediate along the reaction coordinate.
‡
An interchange, I, mechanism could be under either associative or
dissociative activation, i.e., Ia or Id
‡
‡
If the rate of the reaction is strongly dependent on the nature of the entering group
and is weakly dependent on the nature of the leaving group, then bond making is
more important than bond breaking.
The reaction is under associative activation.
We say the mechanism is an Associative Interchange Mechanism, Ia
‡
If the rate of the reaction is weakly dependent on the nature of the entering group
and is strongly dependent on the nature of the leaving group, then bond breaking is
more important than bond making in the approach to the transition state.
The reaction is under dissociative activation.
We say the mechanism is a Dissociative Interchange Mechanism, Id
Ia
Id
Self-exchange reactions
M(H2O)6 + H2O*  M(H2O)5(H2O*) + H2O
(eg., from line shape analysis using 17O NMR)
inert
labile
Rate:
• increases with ionic radius
• decreases with an increase in ionic charge
Rate:
• increases with ionic radius
• decreases with an increase in ionic charge
q
__
Inertness 
r
Inertness  ion
 Self exchange reactions at metal centres are usually
under dissociative activation
For the transition metals...
• Inertness  ion
• Jahn-Teller distortion of high spin d4 and d9 complexes imparts on
them significant lability.
These two will exchange very
rapidly because of the long
(and therefore weak) M-L
bonds.
This is an example of how
a ground state structural
effect can influence
kinetics
• There is a strong correlation between Ligand Field Stabilisation Energy
(LFSE) and inertness
For example, low spin Co3+ and Cr3+ are amongst the most
inert transition metal ions
d3
LFSE =
d6 (LS)
d8
d7 (HS)
d9
d10
-12 Dq
-24Dq + 2P
-12Dq
-8Dq
-6Dq
0
Cr(III)
Co(III)
Ni(II)
Co(II)
Cu(II)
Zn(II)
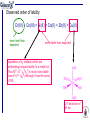
Expected order of lability:
Co(III) < Cr(III) = Ni(II) < Co(II) < Cu(II) < Zn(II)
Expected order of lability:
Co(III) < Cr(III) = Ni(II) < Co(II) < Cu(II) < Zn(II)
Observed order of lability:
Cr(III) ~ Co(III) < Ni(II) < Co(II) < Zn(II) < Cu(II)
more inert than
expected
more labile than expected
Observed order of lability:
Cr(III) ~ Co(III) < Ni(II) < Co(II) < Zn(II) < Cu(II)
more inert than
expected
more labile than expected
population of eg orbitals (which are
antibonding) imparts lability to a metal ion.
Thus Ni2+ (d8, t2g6eg2) is much more labile
than d3 Cr3+ (t2g3) although it has the same
LFSE
J-T distortion of
d9 ion
Hence:
LFSE (a thermodyamic parameter) is a rough guide to the rate
of self-exchange reactions at metal centres (a kinetic
parameter).
2nd and 3rd transition series
Usually very inert
 High LFSE
 Strong M-L bonds because of good overlap between
ligand orbitals and the more expansive (compared to
3d) 4d and 5d orbitals
Clearly the LFSE contributes to the kinetic behaviour of a
metal ion, i.e., there must be a ligand field contribution to the
activation energy (LFAE)
Ground state  Transition state
LFSEGS
LFSETS
LFAE = LFSETS - LFSEGS
EXAMPLE
[Cr(H2O)6]3+  {[Cr(H2O)5(H2O)]3+}‡
LFSEGS = -12Dq
LFSETS
Assumptions:
• the reaction is under dissociative activation
• the departing ligand in the TS is far from the metal centre,
i.e., that the TS is approximately 5-coordinate
The LFSE of the TS will depend on the geometry of the TS, and
two reasonable geometries can be envisaged, viz., square
pyramidal (C4v) and trigonal bipyramidal (D3h)
The LFSE of the TS will depend on the geometry of the TS, and
two reasonable geometries can be envisaged, viz., square
pyramidal (C4v) and trigonal bipyramidal (D3h)
Method of Krishnamurthy and Schaap to estimate LFSE of geometries
that are neither Oh nor Td
D3h
In D3h the d orbitals transform as
e”
e’
a1 ’
xz,yz
x2-y2, xy
z2
Method of Krishnamurthy and Schaap
axial ligand field
equatorial ligand field
axial
equatorial
axial
equatorial
axial
equatorial
axial
equatorial
In D3h the d orbitals transform as
axial
e”
e’
a1’
xz,yz
x2-y2, xy
z2
Symmetry requires the
energies of these two
oribitals to be the same
equatorial
Average of 2.93 and
-4.57 is -0.82
In D3h the d orbitals transform as
axial
e”
e’
a1’
xz,yz
x2-y2, xy
z2
equatorial
7.07Dq
z2, a1'
axial
-0.82 Dq
x2-y2; xy, e'
-2.71 Dq
xz; yz, e"
equatorial
7.07Dq
z2, a1'
-0.82 Dq
x2-y2; xy, e'
-2.71 Dq
xz; yz, e"
LFSETS = 2(-2.71) – 0.82 = -6.24 Dq
LFSEGS = -12Dq
LFAE = -6.24 –(-12) Dq = 5.76 Dq
For Cr(III), Dq = 1760 cm-1 (from electronic spectroscopy), so LFAE=
10138 cm-1
E  h  hc N A
 6.626  1034 Js  2.998  108 ms -1  10138 cm -1 
 2.01 1019 J  6.022  1023 mol-1
= 121 kJ mol-1
100 cm
 NA
m
From this kind of approach:
D Mechanism, D3h intermediate
Cr(III)
-1
LFAE /kJ mol
121
Mn(III)
14
Fe(III)
36
Co(III)
215
Ni(II)
59
D Mechanism, C4v intermediate
Cr(III)
LFAE /kJ mol-1
42
Mn(III)
-39
Fe(III)
36
Co(III)
162
Ni(II)
20
A Mechanism, D5h intermediate
Cr(III)
LFAE /kJ mol-1
89
Mn(III)
67
Fe(III)
12
Co(III)
45
Ni(II)
44
D Mechanism, D3h intermediate
Cr(III)
-1
LFAE /kJ mol
121
Mn(III)
14
Fe(III)
36
Predicted rate:
Co(III) < Cr(III) < Ni(II) < Fe(III) < Mn(III)
Co(III)
215
Ni(II)
59
D Mechanism, C4v intermediate
Cr(III)
-1
LFAE /kJ mol
42
Mn(III)
-39
Fe(III)
36
Predicted rate:
Co(III) < Cr(III) < Fe(III) < Ni(II) < Mn(III)
Co(III)
162
Ni(II)
20
A Mechanism, D5h intermediate
Cr(III)
-1
LFAE /kJ mol
89
Mn(III)
67
Fe(III)
12
Predicted rate:
Cr(III) < Mn(III) < Co(III) ~ Ni(II) < Fe(III)
Co(III)
45
Ni(II)
44
Experimental rate:
Cr(III) < Co(III) < Fe(III) < Ni(II) < Mn(III)
Hence, probably a D mechanism, possibly with a C4v
intermediate.
There is other evidence to suggest that many Cr(III) reactions
have a distinctly associative character, explaining the very
inert nature of Cr(III) complexes