* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Bonding in complexes of d-block metal ions – Crystal Field Theory.
Survey
Document related concepts
Transcript
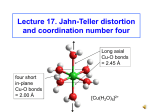
Bonding in complexes of d-block metal ions – Crystal Field Theory. eg energy Δ 3d sub-shell Co3+ ion in gas-phase (d6) d-shell split by presence of ligand donor-atoms t2g Co(III) in complex The d-orbitals: z z y dyz x z y x dxy z y x dxz z y dz2 the t2g set x y dx2-y2 x the eg set Splitting of the d sub-shell in octahedral coordination blue = ligand donor atom orbitals the t2g set z z z y y dyz the egset x the three orbitals of the t2g set lie between the ligand donor-atoms (only dyz shown) dz2 x y dx2-y2 x the two orbitals of the eg set lie along the Cartesian coordinates, and so are adjacent to the donor atoms of the ligands, which raises the eg set in energy Splitting of the d sub-shell in an octahedral complex energy eg Δ 3d sub-shell Co3+ ion in gas-phase (d6) d-shell split by presence of ligand donor-atoms t2g Co(III) in octahedral complex The crystal field splitting parameter (Δ) Different ligands produce different extents of splitting between the eg and the t2g levels. This energy difference is the crystal field splitting parameter Δ, also known as 10Dq, and has units of cm-1. Typically, CN- produces very large values of Δ, while Fproduces very small values. energy eg eg Δ = 26,600 cm-1 Δ = 15,000 cm-1 t2g t2g [Cr(CN)6]3- [CrF6]3- High and low-spin complexes: The d-electrons in d4 to d8 configurations can be high-spin, where they spread out and occupy the whole d sub-shell, or low-spin, where the t2g level is filled first. This is controlled by whether Δ is larger than the spinpairing energy, P, which is the energy required to take pairs of electrons with the same spin orientation, and pair them up with the opposite spin. eg energy Δ>P Paramagnetic 4 unpaired e’s diamagnetic no unpaired e’s t2g eg Δ<P t2g low-spin d6 high-spin d6 electrons fill the t2g level first. In this case the complex is diamagnetic electrons fill the whole d subshell according to Hund’s rule High and low-spin complexes of d5 ions: For d5 ions P is usually very large, so these are mostly high-spin. Thus, Fe(III) complexes are usually high-spin, although with CN- Δ is large enough that [Fe(CN)6]3- is low spin: (CN- always produces the largest Δ values) [Fe(CN)6]3- Δ = 35,000 cm-1 P = 19,000 cm-1 energy [Fe(H2O)6]3+ Δ = 13,700 cm-1 P = 22,000 cm-1 eg Paramagnetic 5 unpaired e’s Δ>P paramagnetic one unpaired e t2g eg Δ<P t2g low-spin d5 ([Fe(CN)6]3-) high-spin d5 ([Fe(H2O)6]3+) electrons fill the t2g level first. In this case the complex is paramagnetic electrons fill the whole d sub-shell according to Hund’s rule High and low-spin complexes of d7 ions: The d7 metal ion that one commonly encounters is the Co(II) ion. For metal ions of the same electronic configuration, Δ tends to increase M(II) < M(III) < M(IV), so that Co(II) complexes have a small Δ and are usually high spin. The (III) ion Ni(III) has higher values of Δ, and is usually low-spin. [Co(H2O)6]2+ Δ = 9,300 cm-1 [Ni(bipy)3]3+ energy eg Paramagnetic 3 unpaired e’s Δ>P paramagnetic one unpaired e t2g low-spin d7 ([Ni(bipy)3]3+) The d-electrons fill the t2g level first, and only then does an electron occupy the eg level. eg Δ<P t2g high-spin d7 ([Co(H2O)6]3+) electrons fill the whole d sub-shell according to Hund’s rule High and low-spin complexes of some d6 ions: For d6 ions Δ is very large for an M(III) ion such as Co(III), so all Co(III) complexes are low-spin except for [CoF6]3-.high-spin. Thus, Fe(III) complexes are usually high-spin, although with CN- Δ is large enough that [Fe(CN)6]3- is low spin: (CN- always produces the largest Δ values) [CoF6]3- Δ = 13,100 cm-1 P = 22,000 cm-1 [Co(CN)6]3- Δ = 34,800 cm-1 P = 19,000 cm-1 eg energy Δ >> P Paramagnetic 4 unpaired e’s diamagnetic no unpaired e’s t2g eg Δ<P t2g low-spin d6 ([Co(CN)6]4-) high-spin d5 ([CoF6]3-) electrons fill the t2g level first. In this case the complex is diamagnetic electrons fill the whole d sub-shell according to Hund’s rule The spectrochemical series: One notices that with different metal ions the order of increasing Δ with different ligands is always the same. Thus, all metal ions produce the highest value of Δ in their hexacyano complex, while the hexafluoro complex always produces a low value of Δ. One has seen how in this course the theme is always a search for patterns. Thus, the increase in Δ with changing ligand can be placed in an order known as the spectrochemical series, which in abbreviated form is: I- < Br- < Cl- < F- < OH- ≈ H2O < NH3 < CN- The spectrochemical series: The place of a ligand in the spectrochemical series is determined largely by its donor atoms. Thus, all N-donor ligands are close to ammonia in the spectrochemical series, while all O-donor ligands are close to water. The spectrochemical series follows the positions of the donor atoms in the periodic table as: C N O F P S Cl ? very little data on P-donors – may be higher than N-donors S-donors ≈ between Br and Cl Br I spectrochemical series follows arrows around starting at I and ending at C The spectrochemical series: Thus, we can predict that O-donor ligands such as oxalate or acetylacetonate will be close to water in the spectrochemical series. It should be noted that while en and dien are close to ammonia in the spectrochemical series, 2,2’bipyridyl and 1,10-phenanthroline are considerably higher than ammonia because their sp2 hybridized N-donors are more covalent in their bonding than the sp3 hybridized donors of ammonia. O O - - O O oxalate H 2N dien N H H 3C CH3 O H 2N O- acetylacetonate NH 2 N bipyridyl N NH 2 en N N 1,10-phen The bonding interpretation of the spectrochemical series: For the first row of donor atoms in the periodic table, namely C, N, O, and F, it is clear that what we are seeing in the variation of Δ is covalence. Thus, C-donor ligands such as CN- and CO produce the highest values of Δ because the overlap between the orbitals of the C-atom and those of the metal are largest. For the highly electronegative F- ion the bonding is very ionic, and overlap is much smaller. For the heavier donor atoms, one might expect from their low electronegativity, more covalent bonding, and hence larger values of Δ. It appears that Δ is reduced in size because of π–overlap from the lone pairs on the donor atom, and the t2g set orbitals, which raises the energy of the t2g set, and so lowers Δ. Crystal Field Stabilization Energy (CFSE): When splitting of the d sub-shell occurs, the occupation of the lower energy t2g level by electrons causes a stabilization of the complex, whereas occupation of the eg level causes a rise in energy. Calculations show that the t2g level drops by 0.4Δ, whereas the eg level is raised by 0.6Δ. This means that the overall change in energy, the CFSE, will be given by: CFSE = Δ(0.4n(t2g) - 0.6n(eg)) where n(t2g) and n(eg) are the numbers of electrons in the t2g and eg levels respectively. Calculation of Crystal Field Stabilization Energy (CFSE): The CFSE for some complexes is calculated to be: [Co(NH3)6]3+: [Cr(en)3]3+ energy eg eg t2g t2g Δ = 22,900 cm-1 Δ = 21,900 cm-1 CFSE = 22,900(0.4 x 6 – 0.6 x 0) = 54,960 cm-1 CFSE = 21,900(0.4 x 3 – 0.6 x 0) = 26,280 cm-1 Crystal Field Stabilization Energy (CFSE) of d5 and d10 ions: The CFSE for high-spin d5 and for d10 complexes is calculated to be zero: [Mn(NH3)6]2+: [Zn(en)3]3+ energy eg eg t2g t2g Δ = 22,900 cm-1 Δ = not known CFSE = 10,000(0.4 x 3 – 0.6 x 2) = 0 cm-1 CFSE = Δ(0.4 x 6 – 0.6 x 4) = 0 cm-1 Crystal Field Stabilization Energy (CFSE) of d0 to d10 M(II) ions: For M(II) ions with the same set of ligands, the variation of Δ is not large. One can therefore use the equation for CFSE to calculate CFSE in terms of Δ for d0 through d10 M(II) ions (all metal ions high-spin): Ca(II) Sc(II) Ti(II) V(II) Cr(II) Mn(II) Fe(II) Co(II) Ni(II) Cu(II) Zn(II) d0 d1 d2 d3 d4 d5 d6 d7 d8 d9 d10 CFSE: 0 0.4Δ 0.8Δ 1.2Δ 0.6Δ 0 0.4Δ 0.8Δ 1.2Δ 0.6Δ 0 This pattern of variation CFSE leads to greater stabilization in the complexes of metal ions with high CFSE, such as Ni(II), and lower stabilization for the complexes of M(II) ions with no CFSE, e.g. Ca(II), Mn(II), and Zn(II). The variation in CFSE can be compared with the log K1 values for EDTA complexes on the next slide: Crystal Field Stabilization Energy (CFSE) of d0 to d10 M(II) ions: CFSE as a function of no of delectrons CFSE in multiples of Δ. 1.4 Ni2+ 1.2 doublehumped curve 1 0.8 0.6 0.4 0.2 Ca2+ 0 0 1 2 Mn2+ 3 4 5 6 7 no of d-electrons Zn2+ 8 9 10 11 Log K1(EDTA) of d0 to d10 M(II) ions: log K1(EDTA) as a function of no of delectrons = CFSE logK1(EDTA). 20 doublehumped curve 18 16 Zn2+ 14 Mn2+ 12 Ca2+ 10 0 1 2 3 4 5 6 rising baseline due to ionic contraction 7 no of d-electrons 8 9 10 11 Log K1(en) of d0 to d10 M(II) ions: log K1(en) as a function of no of delectrons = CFSE 12 doublehumped curve logK1(en). 10 8 6 Zn2+ 4 Ca2+ 2 rising baseline due to ionic contraction Mn2+ 0 0 1 2 3 4 5 6 7 no of d-electrons 8 9 10 11 Log K1(tpen) of d0 to d10 M(II) ions: log K1(tpen) as a function of no of delectrons doublehumped curve logK1(tpen). 20 15 Zn2+ 10 Mn2+ 5 N N N N N tpen N Ca2+ 0 0 1 2 3 4 5 6 7 no of d-electrons 8 9 10 11 The Irving-Williams Stability Order: Irving and Williams noted that because of CFSE, the log K1 values for virtually all complexes of first row d-block metal ions followed the order: Mn(II) < Fe(II) < Co(II) < Ni(II) < Cu(II) > Zn(II) We see that this order holds for the ligand EDTA, en, and TPEN on the previous slides. One notes that Cu(II) does not follow the order predicted by CFSE, which would have Ni(II) > Cu(II). This will be discussed under JahnTeller distortion of Cu(II) complexes, which leads to additional stabilization for Cu(II) complexes over what would be expected from the variation in CFSE.