Download Bonding in complexes of d-block metal ions – Crystal Field Theory.

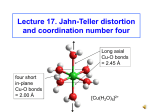
Bonding in complexes of d-block
metal ions – Crystal Field Theory.
eg
energy
Δ
3d sub-shell
Co3+ ion
in gas-phase
(d6)
d-shell
split by
presence
of ligand
donor-atoms
t2g
Co(III) in
complex
The d-orbitals:
z
z
y
dyz
x
z
y
x
dxy
z
y
x
dxz
z
y
dz2
the t2g
set
x
y
dx2-y2
x
the eg
set
Splitting of the d sub-shell in
octahedral coordination
blue = ligand donor
atom orbitals
the t2g set
z
z
z
y
y
dyz
the egset
x
the three orbitals of
the t2g set lie between
the ligand donor-atoms
(only dyz shown)
dz2
x
y
dx2-y2
x
the two orbitals of the eg set lie along the
Cartesian coordinates, and so are adjacent
to the donor atoms of the ligands, which
raises the eg set in energy
Splitting of the d sub-shell in
an octahedral complex
energy
eg
Δ
3d sub-shell
Co3+ ion
in gas-phase
(d6)
d-shell
split by
presence
of ligand
donor-atoms
t2g
Co(III) in
octahedral
complex
The crystal field splitting parameter (Δ)
Different ligands produce different extents of splitting between
the eg and the t2g levels. This energy difference is the crystal
field splitting parameter Δ, also known as 10Dq, and has units
of cm-1. Typically, CN- produces very large values of Δ, while Fproduces very small values.
energy
eg
eg
Δ = 26,600 cm-1
Δ = 15,000 cm-1
t2g
t2g
[Cr(CN)6]3-
[CrF6]3-
High and low-spin complexes:
The d-electrons in d4 to d8 configurations can be high-spin, where they
spread out and occupy the whole d sub-shell, or low-spin, where the t2g
level is filled first. This is controlled by whether Δ is larger than the spinpairing energy, P, which is the energy required to take pairs of electrons
with the same spin orientation, and pair them up with the opposite spin.
eg
energy
Δ>P
Paramagnetic
4 unpaired e’s
diamagnetic
no unpaired e’s
t2g
eg
Δ<P
t2g
low-spin d6
high-spin d6
electrons fill the t2g level first. In this
case the complex is diamagnetic
electrons fill the whole d subshell according to Hund’s rule
High and low-spin complexes of d5 ions:
For d5 ions P is usually very large, so these are mostly high-spin. Thus,
Fe(III) complexes are usually high-spin, although with CN- Δ is large enough
that [Fe(CN)6]3- is low spin: (CN- always produces the largest Δ values)
[Fe(CN)6]3- Δ = 35,000 cm-1
P = 19,000 cm-1
energy
[Fe(H2O)6]3+ Δ = 13,700 cm-1
P = 22,000 cm-1
eg
Paramagnetic
5 unpaired e’s
Δ>P
paramagnetic
one unpaired e
t2g
eg
Δ<P
t2g
low-spin d5 ([Fe(CN)6]3-)
high-spin d5 ([Fe(H2O)6]3+)
electrons fill the t2g level first. In this
case the complex is paramagnetic
electrons fill the whole d sub-shell
according to Hund’s rule
High and low-spin complexes of d7 ions:
The d7 metal ion that one commonly encounters is the Co(II) ion. For metal
ions of the same electronic configuration, Δ tends to increase M(II) < M(III) <
M(IV), so that Co(II) complexes have a small Δ and are usually high spin.
The (III) ion Ni(III) has higher values of Δ, and is usually low-spin.
[Co(H2O)6]2+ Δ = 9,300 cm-1
[Ni(bipy)3]3+
energy
eg
Paramagnetic
3 unpaired e’s
Δ>P
paramagnetic
one unpaired e
t2g
low-spin d7 ([Ni(bipy)3]3+)
The d-electrons fill the t2g level first,
and only then does an electron
occupy the eg level.
eg
Δ<P
t2g
high-spin d7 ([Co(H2O)6]3+)
electrons fill the whole d sub-shell
according to Hund’s rule
High and low-spin complexes of some d6 ions:
For d6 ions Δ is very large for an M(III) ion such as Co(III), so all Co(III)
complexes are low-spin except for [CoF6]3-.high-spin. Thus,
Fe(III) complexes are usually high-spin, although with CN- Δ is large enough
that [Fe(CN)6]3- is low spin: (CN- always produces the largest Δ values)
[CoF6]3- Δ = 13,100 cm-1
P = 22,000 cm-1
[Co(CN)6]3- Δ = 34,800 cm-1
P = 19,000 cm-1
eg
energy
Δ >> P
Paramagnetic
4 unpaired e’s
diamagnetic
no unpaired e’s
t2g
eg
Δ<P
t2g
low-spin d6 ([Co(CN)6]4-)
high-spin d5 ([CoF6]3-)
electrons fill the t2g level first. In this
case the complex is diamagnetic
electrons fill the whole d sub-shell
according to Hund’s rule
The spectrochemical series:
One notices that with different metal ions the order of
increasing Δ with different ligands is always the same.
Thus, all metal ions produce the highest value of Δ in
their hexacyano complex, while the hexafluoro complex
always produces a low value of Δ. One has seen how in
this course the theme is always a search for patterns.
Thus, the increase in Δ with changing ligand can be
placed in an order known as the spectrochemical series,
which in abbreviated form is:
I- < Br- < Cl- < F- < OH- ≈ H2O < NH3 < CN-
The spectrochemical series:
The place of a ligand in the spectrochemical series is determined
largely by its donor atoms. Thus, all N-donor ligands are close to
ammonia in the spectrochemical series, while all O-donor ligands
are close to water. The spectrochemical series follows the positions
of the donor atoms in the periodic table as:
C
N
O
F
P
S
Cl
?
very little
data on
P-donors –
may be higher
than N-donors
S-donors ≈
between Br
and Cl
Br
I
spectrochemical
series follows
arrows around
starting at I and
ending at C
The spectrochemical series:
Thus, we can predict that O-donor ligands such as oxalate or
acetylacetonate will be close to water in the spectrochemical series.
It should be noted that while en and dien are close to ammonia in
the spectrochemical series, 2,2’bipyridyl and 1,10-phenanthroline
are considerably higher than ammonia because their sp2 hybridized
N-donors are more covalent in their bonding than the sp3 hybridized
donors of ammonia.
O
O
-
-
O
O
oxalate
H 2N
dien
N
H
H 3C
CH3
O
H 2N
O-
acetylacetonate
NH 2
N
bipyridyl
N
NH 2
en
N
N
1,10-phen
The bonding interpretation of
the spectrochemical series:
For the first row of donor atoms in the periodic table,
namely C, N, O, and F, it is clear that what we are seeing
in the variation of Δ is covalence. Thus, C-donor ligands
such as CN- and CO produce the highest values of Δ
because the overlap between the orbitals of the C-atom
and those of the metal are largest. For the highly
electronegative F- ion the bonding is very ionic, and
overlap is much smaller. For the heavier donor atoms,
one might expect from their low electronegativity, more
covalent bonding, and hence larger values of Δ. It
appears that Δ is reduced in size because of π–overlap
from the lone pairs on the donor atom, and the t2g set
orbitals, which raises the energy of the t2g set, and so
lowers Δ.
Crystal Field Stabilization
Energy (CFSE):
When splitting of the d sub-shell occurs, the occupation
of the lower energy t2g level by electrons causes a
stabilization of the complex, whereas occupation of the
eg level causes a rise in energy. Calculations show that
the t2g level drops by 0.4Δ, whereas the eg level is raised
by 0.6Δ. This means that the overall change in energy,
the CFSE, will be given by:
CFSE = Δ(0.4n(t2g)
-
0.6n(eg))
where n(t2g) and n(eg) are the numbers of electrons in
the t2g and eg levels respectively.
Calculation of Crystal Field
Stabilization Energy (CFSE):
The CFSE for some complexes is calculated to be:
[Co(NH3)6]3+:
[Cr(en)3]3+
energy
eg
eg
t2g
t2g
Δ = 22,900 cm-1
Δ = 21,900 cm-1
CFSE = 22,900(0.4 x 6 – 0.6 x 0)
= 54,960 cm-1
CFSE = 21,900(0.4 x 3 – 0.6 x 0)
=
26,280 cm-1
Crystal Field Stabilization Energy
(CFSE) of d5 and d10 ions:
The CFSE for high-spin d5 and for d10 complexes is
calculated to be zero:
[Mn(NH3)6]2+:
[Zn(en)3]3+
energy
eg
eg
t2g
t2g
Δ = 22,900 cm-1
Δ = not known
CFSE = 10,000(0.4 x 3 – 0.6 x 2)
= 0 cm-1
CFSE = Δ(0.4 x 6 – 0.6 x 4)
=
0 cm-1
Crystal Field Stabilization Energy
(CFSE) of d0 to d10 M(II) ions:
For M(II) ions with the same set of ligands, the variation of Δ is not large.
One can therefore use the equation for CFSE to calculate CFSE in terms of
Δ for d0 through d10 M(II) ions (all metal ions high-spin):
Ca(II) Sc(II) Ti(II) V(II) Cr(II) Mn(II) Fe(II) Co(II) Ni(II) Cu(II) Zn(II)
d0
d1
d2
d3
d4
d5
d6
d7
d8
d9
d10
CFSE: 0
0.4Δ
0.8Δ
1.2Δ 0.6Δ
0
0.4Δ
0.8Δ
1.2Δ 0.6Δ
0
This pattern of variation CFSE leads to greater stabilization in the complexes
of metal ions with high CFSE, such as Ni(II), and lower stabilization for the
complexes of M(II) ions with no CFSE, e.g. Ca(II), Mn(II), and Zn(II). The
variation in CFSE can be compared with the log K1 values for EDTA
complexes on the next slide:
Crystal Field Stabilization Energy (CFSE) of
d0 to d10 M(II) ions:
CFSE as a function of no of delectrons
CFSE in multiples of Δ.
1.4
Ni2+
1.2
doublehumped
curve
1
0.8
0.6
0.4
0.2
Ca2+
0
0
1
2
Mn2+
3
4
5
6
7
no of d-electrons
Zn2+
8
9
10 11
Log K1(EDTA) of d0 to d10 M(II) ions:
log K1(EDTA) as a function of no of delectrons
= CFSE
logK1(EDTA).
20
doublehumped
curve
18
16
Zn2+
14
Mn2+
12
Ca2+
10
0
1
2
3
4
5
6
rising baseline
due to ionic
contraction
7
no of d-electrons
8
9
10 11
Log K1(en) of d0 to d10 M(II) ions:
log K1(en) as a function of no of delectrons
= CFSE
12
doublehumped
curve
logK1(en).
10
8
6
Zn2+
4
Ca2+
2
rising baseline
due to ionic
contraction
Mn2+
0
0
1
2
3
4
5
6
7
no of d-electrons
8
9
10 11
Log K1(tpen) of d0 to d10 M(II) ions:
log K1(tpen) as a function of no of delectrons
doublehumped
curve
logK1(tpen).
20
15
Zn2+
10
Mn2+
5
N
N
N
N
N
tpen
N
Ca2+
0
0
1
2
3
4
5
6
7
no of d-electrons
8
9
10 11
The Irving-Williams Stability Order:
Irving and Williams noted that because of CFSE, the log
K1 values for virtually all complexes of first row d-block
metal ions followed the order:
Mn(II) < Fe(II) < Co(II) < Ni(II) < Cu(II) > Zn(II)
We see that this order holds for the ligand EDTA, en, and
TPEN on the previous slides. One notes that Cu(II) does
not follow the order predicted by CFSE, which would
have Ni(II) > Cu(II). This will be discussed under JahnTeller distortion of Cu(II) complexes, which leads to
additional stabilization for Cu(II) complexes over what
would be expected from the variation in CFSE.