* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Lecture 2 - City University of New York
Survey
Document related concepts
Transcript
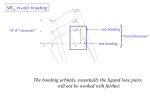
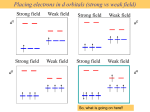
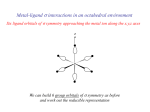
ML6 s-only bonding “d0-d10 electrons” anti bonding “metal character” non bonding 6 s ligands x 2e each The bonding orbitals, essentially the ligand lone pairs, 12 s bondingwill e not be worked with further. “ligand character” π-bonding may be introduced as a perturbation of the t2g/eg set: Case 1 (CN-, CO, C2H4) empty π-orbitals on the ligands ML π-bonding (π-back bonding) t2g (π*) These are the SALC formed from the p orbitals of the ligands that can interac with the d on the metal. t2g eg eg Do D’o Do has increased t2g Stabilization t2g (π) ML6 s-only ML6 s+π (empty π-orbitals on ligands) π-bonding may be introduced as a perturbation of the t2g/eg set. Case 2 (Cl-, F-) filled π-orbitals on the ligands LM π-bonding eg Do has decreased eg D’o t2g (π*) Do Destabilization t2g t2g Stabilization t2g (π) ML6 s-only ML6 s+π (filled π-orbitals) Putting it all on one diagram. Strong field / low spin Weak field / high spin Spectrochemical Series Purely s ligands: D: en > NH3 (order of proton basicity) donating which decreases splitting and causes high spin: D: H2O > F > RCO2 > OH > Cl > Br > I (also proton basicity) accepting ligands increase splitting and may be low spin D: CO, CN-, > phenanthroline > NO2- > NCS- Merging to get spectrochemical series CO, CN- > phen > en > NH3 > NCS- > H2O > F- > RCO2- > OH- > Cl- > Br- > I- Strong field, acceptors large D low spin s only Weak field, donors small D high spin Turning to Square Planar Complexes z y x Most convenient to use a local coordinate system on each ligand with y pointing in towards the metal. py to be used for s bonding. z being perpendicular to the molecular plane. pz to be used for bonding perpendicular to the plane, ^. x lying in the molecular plane. px to be used for bonding in the molecular plane, |. ML4 square planar complexes ligand group orbitals and matching metal orbitals s bonding bonding (in) bonding (perp) ML4 square planar complexes MO diagram eg s-only bonding Sample bonding Angular Overlap Method An attempt to systematize the interactions for all geometries. 1 1 4 M 7 8 3 11 M M 2 9 5 6 2 12 10 6 The various complexes may be fashioned out of the ligands above Linear: 1,6 Tetrahedral: 7,8,9,10 Trigonal: 2,11,12 Square planar: 2,3,4,5 T-shape: 1,3,5 Trigonal bipyramid: 1,2,6,11,12 Square pyramid: 1,2,3,4,5 Octahedral: 1,2,3,4,5,6 Cont’d All s interactions with the ligands are stabilizing to the ligands and destabilizing to the d orbitals. The interaction of a ligand with a d orbital depends on their orientation with respect to each other, estimated by their overlap which can be calculated. The total destabilization of a d orbital comes from all the interactions with the set of ligands. For any particular complex geometry we can obtain the overlaps of a particular d orbital with all the various ligands and thus the destabilization. ligand dz2 dx2-y2 dxy dxz dyz 1 1 es 0 0 0 0 2 ¼ ¾ 0 0 0 3 ¼ ¾ 0 0 0 4 ¼ ¾ 0 0 0 5 ¼ ¾ 0 0 0 6 1 0 0 0 0 7 0 0 1/3 1/3 1/3 8 0 0 1/3 1/3 1/3 9 0 0 1/3 1/3 1/3 10 0 0 1/3 1/3 1/3 11 ¼ 3/16 9/16 0 0 12 1/4 3/16 9/16 0 0 Thus, for example a dx2-y2 orbital is destabilized by (3/4 +6/16) es = 18/16 es in a trigonal bipyramid complex due to s interaction. The dxy, equivalent by symmetry, is destabilized by the same amount. The dz2 is destabililzed by 11/4 es. Coordination Chemistry Electronic Spectra of Metal Complexes Electronic spectra (UV-vis spectroscopy) Electronic spectra (UV-vis spectroscopy) hn DE The colors of metal complexes Electronic configurations of multi-electron atoms What is a 2p2 configuration? n = 2; l = 1; ml = -1, 0, +1; ms = ± 1/2 Many configurations fit that description These configurations are called microstates and they have different energies because of inter-electronic repulsions Electronic configurations of multi-electron atoms Russell-Saunders (or LS) coupling For each 2p electron n = 1; l = 1 ml = -1, 0, +1 ms = ± 1/2 For the multi-electron atom L = total orbital angular momentum quantum number S = total spin angular momentum quantum number Spin multiplicity = 2S+1 ML = ∑ml (-L,…0,…+L) MS = ∑ms (S, S-1, …,0,…-S) ML/MS define microstates and L/S define states (collections of microstates) Groups of microstates with the same energy are called terms Determining the microstates for p2 Spin multiplicity 2S + 1 Determining the values of L, ML, S, Ms for different terms 1S 1P Classifying the microstates for p2 Largest ML is +2, so L = 2 (a D term) and MS = 0 for ML = +2, 2S +1 = 1 (S = 0) 1D Next largest ML is +1, so L = 1 (a P term) and MS = 0, ±1/2 for ML = +1, 2S +1 = 3 3P Spin multiplicity = # columns of microstates One remaining microstate ML is 0, L = 0 (an S term) and MS = 0 for ML = 0, 2S +1 = 1 1S Largest ML is +2, so L = 2 (a D term) and MS = 0 for ML = +2, 2S +1 = 1 (S = 0) 1D Next largest ML is +1, so L = 1 (a P term) and MS = 0, ±1/2 for ML = +1, 2S +1 = 3 3P ML is 0, L = 0 2S +1 = 1 1S Energy of terms (Hund’s rules) Lowest energy (ground term) Highest spin multiplicity 3P term for p2 case 3P has S = 1, L = 1 If two states have the same maximum spin multiplicity Ground term is that of highest L Determining the microstates for s1p1 Determining the terms for s1p1 Ground-state term Coordination Chemistry Electronic Spectra of Metal Complexes cont. Electronic configurations of multi-electron atoms Russell-Saunders (or LS) coupling For each 2p electron n = 1; l = 1 ml = -1, 0, +1 ms = ± 1/2 For the multi-electron atom L = total orbital angular momentum quantum number S = total spin angular momentum quantum number Spin multiplicity = 2S+1 ML = ∑ml (-L,…0,…+L) MS = ∑ms (S, S-1, …,0,…-S) ML/MS define microstates and L/S define states (collections of microstates) Groups of microstates with the same energy are called terms before we did: p2 ML & MS Microstate Table States (S, P, D) Spin multiplicity Terms 3P, 1D, 1S Ground state term 3P For metal complexes we need to consider d1-d10 d2 3F, 3P, 1G, 1D, 1S For 3 or more electrons, this is a long tedious process But luckily this has been tabulated before… Transitions between electronic terms will give rise to spectra Selection rules (determine intensities) Laporte rule g g forbidden (that is, d-d forbidden) but g u allowed (that is, d-p allowed) Spin rule Transitions between states of different multiplicities forbidden Transitions between states of same multiplicities allowed These rules are relaxed by molecular vibrations, and spin-orbit coupling Group theory analysis of term splitting An e electron superimposed on a spherical distribution energies reversed because tetrahedral High Spin Ground States Holes in d5 and d10, reversing energies relative to d1 dn Free ion GS Oct. complex Tet complex d0 1S t2g0eg0 e0t20 d1 2D t2g1eg0 e1t20 d2 3F t2g2eg0 e2t20 d3 4F t2g3eg0 e2t21 d4 5D t2g3eg1 e2t22 d5 6S t2g3eg2 e2t23 d6 5D t2g4eg2 e3t23 d7 4F t2g5eg2 e4t23 d8 3F t2g6eg2 e4t24 d9 2D t2g6eg3 e4t25 d10 1S t2g6eg4 e4t26 dn d10-n dn d5+n; Holes: = and neglecting spin = same splitting but reversed energies because positive. Expect oct d1 and d6 to behave same as tet d4 and d9 Expect oct d4 and d9 (holes), tet d1 and d6 to be reverse of oct d1 A t2 hole in d5, reversed energies, reversed again relative to octahedral since tet. d1 d6 d4 d9 Orgel diagram for d1, d4, d6, d9 Eg or E T2g or T2 Energy D T2g or T2 Eg or E D d1, d6 tetrahedral d4, d9 octahedral 0 d1, d6 octahedral d4, d9 tetrahedral ligand field strength D Orgel diagram for d2, d3, d7, d8 ions Energy A2 or A2g T1 or T1g T1 or T1g P T1 or T1g T2 or T2g F T2 or T2g T1 or T1g A2 or A2g d2, d7 tetrahedral 0 d2, d7 octahedral d3, d8 octahedral d3, d8 tetrahedral Ligand field strength (Dq) d2 3F, 3P, 1G, 1D, 1S Real complexes Tanabe-Sugano diagrams Electronic transitions and spectra Other configurations d3 d9 d1 d2 d8 Other configurations d3 The limit between high spin and low spin Determining Do from spectra d1 d9 One transition allowed of energy Do Determining Do from spectra mixing mixing Lowest energy transition = Do Ground state is mixing E (T1gA2g) - E (T1gT2g) = Do The d5 case All possible transitions forbidden Very weak signals, faint color Some examples of spectra Charge transfer spectra Metal character LMCT Ligand character Ligand character MLCT Metal character Much more intense bands