Download T 2g

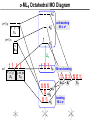
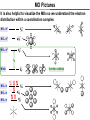
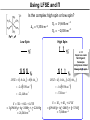
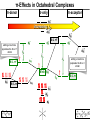
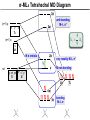
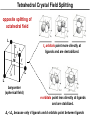
Coordination Chemistry II:
Ligand Field Theory
Chapter 10
Friday, November 22, 2013
Ligand Field Theory
In LFT we use metal valence orbitals and ligand frontier orbitals to
make metal–ligand molecular orbitals
Metal valence orbitals:
Sc – Zn
3d
4s
4p
4d
5s
5p
Y – Cd
Ligand frontier orbital:
La – Hg
5d
6s
6p
Oh first!
We already did this: see 10/18 lecture.
For now we will only consider
σ-bonding with the ligands
σ-MOs for Octahedral Complexes
We use group theory to understand how metal and σ-ligand orbitals
interact in a complex:
nd
(n+1)s
z2 x2–y2 xy xz yz
Eg
T2g
s
A1g
(n+1)p
x
y z
T1u
Oh
symmetries (irr. reps.) of
the metal valence
orbitals are obtained
directly from the
character table
We need to determine the reducible representation for the σ-ligand
orbitals in Oh:
C2′ C4
S4
C2
σh
Γσ
the total ligand
representation (Γ6L) can
be decomposed as we
learned in 4.4.2
E
8C3
6C2
6C4
3C2′
i
6S4
8S6
3σh
6σd
irreducible
representations
6
0
0
2
2
0
0
0
4
2
A1g + Eg + T1u
σ-ML6 Octahedral MO Diagram
t1u*
(n+1)p
x
y z
T1u
a1g*
(n+1)s
anti-bonding
M–L σ*
eg*
s
A1g
Δo
nd
z2 x2–y2 xy xz yz
Eg
T2g
t2g
M non-bonding
A1g
t1u
a1g
eg
bonding
M–L σ
Eg
T1u
MO Pictures
It is also helpful to visualize the MOs so we understand the electron
distribution within a coordination complex
M–L σ*
t1u*
M–L σ*
a1g*
M–L σ*
eg*
∆O
M nb
t2g
M–L σ
t1u
M–L σ
M–L σ
a1g
eg
frontier orbitals
Adding Metal Electrons
t1u*
a1g*
eg*
t2g
t1u
a1g
eg
Metal ions typically have some valence electrons that
can be accommodated in the metal d orbitals
•
d0 ions – Ti4+, Zr4+, V5+, Ta5+, Cr6+, Mo6+, etc.
•
d1 ions – Ti3+, V4+, Ta4+, Cr5+, Mo5+, etc.
•
d2 ions – V3+, Ta3+, Cr4+, Mo4+, etc.
•
d3 ions – V2+, Ta2+, Cr3+, Mo3+, Mn4+, etc.
•
d4-d7 – hold on
•
d8 ions – Co1+, Ni2+, Cu3+, etc.
•
d9 ions – Ni1+, Cu2+, etc.
•
d10 ions – Cu1+, Zn2+, etc.
High Spin and Low Spin
t1u*
a1g*
a1g*
•d4
ions – Cr2+, Mo2+, Mn3+, Fe4+, Ru4+, etc.
eg*
•d5
ions – Mn2+, Re2+, Fe3+, Ru3+, etc.
•d6
ions – Fe2+, Ru2+, Co3+, Rh3+, Pt4+, etc.
t2g
t2g
•d7
a1g
eg
For
ions – Fe1+, Ru1+, Co2+, Rh2+, Ni3+, etc.
d4-d7
electron counts:
•
when ∆o > Πtotal ➙ low spin
•
when ∆o < Πtotal ➙ high spin
t1u
a1g
eg
LOW SPIN
HIGH SPIN
eg*
t1u
t1u*
The situation is a little more
complicated for d4-d7 metals:
High Spin and Low Spin
Electron configurations for octahedral complexes, e.g. [M(H2O)6]+n.
Only the d4 through d7 cases can be either high-spin or low spin.
Δ<Π
Δ>Π
Weak-field ligands:
- Small Δ, High spin complexes
Strong-field ligands:
- Large Δ, Low spin complexes
Electron Pairing Energy
The total electron pairing energy, Πtotal, has two components, Πc and
Πe
•
Πc is a destabilizing energy for the Coulombic repulsion associated with putting two
electrons into the same orbital
•
Πe is a stabilizing energy for electron exchange associated with two electrons
having parallel spin
d4 HS
d8
eg*
d6 LS
eg*
eg*
Πe only counts for
electrons at the
same energy!
t2g
t2g
t2g
total  3e  0c
total  7e  3c
total  6e  3c
LFSE  30.4 O   10.6 O 
 0.6 O
LFSE  6 0.4 O   2 0.6 O 
 1.2 O
LFSE  6 0.4 O   0 0.6 O 
 2.4 O
Using LFSE and Π
Is the complex high spin or low spin?
Δ𝑜 = 9,350𝑐𝑚−1
Π𝑐 = 19,600𝑐𝑚−1
Π𝑒 = −2,000𝑐𝑚−1
Fe2+, d6
Low Spin
High Spin
eg*
eg*
t2g
LFSE  6 0.4 O  0 0.6 O 

 2.4 9350cm 1

 22, 440cm 1
𝐸 = 3Π𝑐 + 6Π𝑒 + 𝐿𝐹𝑆𝐸
= 3 19600 + 6 −2000 + −22400
= 24,360𝑐𝑚−1
Δ<Π
Aqua is a weak
field ligand;
hexaaqua
complexes almost
always high spin
t2g
LFSE  4 0.4 O   2 0.6 O 

 0.4 9350cm 1

 3740cm 1
𝐸 = 1Π𝑐 + 4Π𝑒 + 𝐿𝐹𝑆𝐸
= 19600 + 4 −2000 + −3740
= 7,860𝑐𝑚−1
π-MOs for Octahedral Complexes
The reducible representation for the π-ligand orbitals in Oh:
x and y axes
on each ligand
Γπ
E
8C3
6C2
6C4
3C2′
i
6S4
8S6
3σh
6σd
irreducible
representations
12
0
0
0
-4
0
0
0
0
0
T1g + T2g + T1u + T2u
The non-bonding t2g orbitals of an octahedral metal complex are
oriented perfectly to form π-bonds with ligands
π Donor vs π Acceptor Ligands
The nature of the metal ligand π interaction is dependent on the type
of ligand.
•
π-donor ligands are ligands with one or more lone pairs of electrons in p orbitals on
the donor atom that can donate to empty orbitals on the metal.
•
preferred for metals with high oxidation states and low d electron count (d0-d3)
Examples:
Cl–, Br–, I–, OR–, SR–,
NR2–, O2–, NR2–, N3–
•
π-acceptor ligands (π-acidic ligands) are ligands with empty π* orbitals on the
donor atom that can accept electrons from the metal.
•
preferred for metals with low oxidation states and high d electron count (d6 or higher)
•
donation of electron density from the metal to the ligand π* orbital results in weakening of the multiple
ligand bond
Examples:
CO, NO, CN-, pyridine
“π back bonding”
π-Effects in Octahedral Complexes
σ-only
π-donor
π-acceptor
t1u*
increasing ∆O
a1g*
adding d electrons
populates the M–L π*
orbital
M–L π*
eg*
eg*
t2g*
M–L π*
t2g*
∆o
∆o
∆o
t2g*
M nb t2g
t2g
t2g
M–L π
eg*
t2g
t1u
a1g
eg
adding d electrons
populates the M–L π
orbital
M–L π
π-Effects in Octahedral Complexes
strong field,
low spin
weak field,
high spin
Spectrochemical Series
The trend in ∆O that arises from π-donor, σ-only, and π-acceptor
ligands is the basis for the Spectrochemical Series. For [ML6]n+
complexes:
increasing ∆O
I– < Br– < Cl– < OH– < RCO2– < F– < H2O < NCS– < NH3 < en < NO2– < phen < CN– ≅ CO
π donor ligands
σ only ligands
π acceptor ligands
•
•
weak-field ligands
high-spin complexes for 3d
metals*
•
•
strong-field ligands
low-spin complexes for 3d
metals*
The value of Δo also depends systematically on the metal:
1. Δo increases with increasing oxidation number.
2. Δo increases down a group.
→ both trends are due to stronger metal-ligand bonding.
* Due to effect #2, octahedral 3d metal complexes can be low spin or
high spin, but 4d and 5d metal complexes are always low spin.
σ-MOs for Tetrahedral Complexes
Four-coordinate tetrahedral complexes are ubiquitous throughout the
transition metals.
nd
(n+1)s
z2 x2–y2 xy xz yz
E
T2
s
A1
(n+1)p
x
y
T2
z
the irr. reps. of the metal
valence orbitals are
obtained directly from the
character table
Td
For the ligand orbitals we need to consider how the Lewis base pairs
transform in the Td point group. The result is:
Γσ = A1 + T2
A1
T2
σ-ML4 Tetrahedral MO Diagram
3t2
(n+1)p
x
y
T2
2a1
z
4
t  o
9
(n+1)s
s
A1
M d orbitals
2t2
very weakly M–L σ*
∆t
e
nd
xy xz yz
T2
M non-bonding
z2 x2–y2
E
A1
1a1
1t2
bonding
M–L σ
T2
Tetrahedral Complexes
•
Metal d orbitals are split into a non-bonding E set and a very weakly anti-bond T2 set
•
tetrahedral geometry can accommodate all d electron counts, from d0 to d10
eg*
very weakly M–L σ*
t2
*
strongly M–L σ*
∆o
∆t
M non-bonding
e
t2g M non-bonding
4
t  o
9
•
Δt is small compared to Δo:
•
All tetrahedral complexes of the 3d transition metals are HIGH SPIN!
•
Tetrahedral complexes of the heavier transition metals are low spin.
Tetrahedral Crystal Field Splitting
opposite splitting of
octahedral field
L
z
M
t2 orbitals point more directly at
ligands and are destabilized.
L
y
x
L
L
barycenter
(spherical field)
e orbitals point less directly at ligands
and are stabilized.
Δt < Δo because only 4 ligands and d orbitals point between ligands