* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Nonoverlap of the Star Unfolding
Duality (mathematics) wikipedia , lookup
Dessin d'enfant wikipedia , lookup
Line (geometry) wikipedia , lookup
Tessellation wikipedia , lookup
Euclidean geometry wikipedia , lookup
Planar separator theorem wikipedia , lookup
Apollonian network wikipedia , lookup
Signed graph wikipedia , lookup
List of regular polytopes and compounds wikipedia , lookup
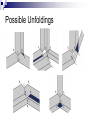
Local Overlaps in Unfoldings of Polyhedra Brendan Lucier Anna Lubiw University of Waterloo Presented at the 15th Annual Fall Workshop on Computational Geometry, 2005 University of Pennsylvania, Philadelphia, PA Local Overlaps in Unfoldings of Polyhedra Brendan Lucier Anna Lubiw University of Waterloo Presented at the 15th Annual Fall Workshop on Computational Geometry, 2005 University of Pennsylvania, Philadelphia, PA Outline Introduction Avoidability of 1-Local Overlaps Small Ununfoldable Polyhedron Outline Introduction Avoidability of 1-Local Overlaps Small Ununfoldable Polyhedron Unfolding Polyhedra We consider the act of cutting a polyhedron along its edges and unfolding it into the plane. The resulting planar figure is an edge unfolding. Two faces of the unfolding overlap if they have a common interior point. An unfolding with no overlap is a simple unfolding, or net. A polyhedron with no net is referred to as ununfoldable. Locality of Overlaps One problem in studying overlaps is that two faces in vastly different parts of a polyhedron could intersect in an unfolding. We propose a definition of locality of an overlap. An overlap is k-local if the overlapping faces are connected by a path of k vertices. In particular, an overlap is 1-local if the overlapping faces are coincident with a vertex in the unfolding. 2-local overlap 1-local overlap Outline Introduction Avoidability of 1-Local Overlaps Small Ununfoldable Polyhedron Describing 1-Local Overlaps A 1-local overlap corresponds precisely to a situation in which a vertex in an unfolding has total face angle greater than 2π. To create such an overlap, we must start with a vertex in the polyhedron with negative curvature, then cut in such a way that one image of the vertex will retain at least 2π of the surface material. Convex polyhedra clearly avoid 1-local overlaps, since they contain no vertices with negative curvature. Motivating Question: does every polyhedron admit an unfolding that contains no 1-local overlaps? No! Four-Pointed Star Our polyhedron is a 4-pointed star. The polyhedron is parameterized: α is the length of each spike. β is the height of the center points. The parameter values are not important, aside from considering alpha to be sufficiently large and beta sufficiently small. Argument Claim: every unfolding of the fourpointed star contains a 1-local overlap. Each of the four B vertices has four face angles, each larger than 2π/3. If three of these faces appeared in one component of an unfolding, we have a 1-local overlap To prevent this, we must cut at least two opposing edges incident to each B vertex. Argument (con’t) Our cuts cannot make a cycle, otherwise we get a disconnected unfolding. So no two pairs of opposing cuts can be made to the middle vertices. Also, not all pairs can be made to the points of the star. The cuts must therefore be made as shown in the bottom diagram. There is only one more cut that can be made, since the set of all cuts must make a spanning tree over all vertices. Argument (con’t) Note that the center vertices have negative curvature (they form saddles). Each must have at least 2 incident cuts, otherwise all the face angles will go to one component and form a 1-local overlap. However, our remaining cut cannot be incident with both center vertices, since they are not adjacent. It is therefore impossible to cut our 4-pointed star to avoid 1-local overlaps. Outline Introduction (Un)avoidability of 1-Local Overlaps A Small Ununfoldable Polyhedron Creating a Smaller Example The 4-Pointed Star is an ununfoldable polyhedron with 16 triangular faces. We shall now make modifications to create a smaller polyhedron. This polyhedron will remain ununfoldable, but will avoid 1-local overlaps. The result will be a starlike ununfoldable polyhedron with 9 faces. Modification #1: 3-Pointed Star Modification #2: Flatten One side of the polyhedron is flattened. Two triangular faces are combined into a single quadrilateral face. Think of the operation as “cutting” the polyhedron into two halves, lengthwise. This introduces the degeneracy of coplanar faces, but this can be fixed by sufficiently small perturbation. Modification #3: Asymmetricize Perturb the symmetry of the points by increasing the angle between two points. This adds a new parameter, φ, indicating the angle change. We do this to increase the face angles at two of the B vertices to larger than 2π/3. Perturbing by φ = 10o is sufficient. Unfolding This Polyhedron At the B vertices with face angles greater than 2π/3, two opposing edges must be cut. Two cuts must be incident with the top center vertex, as it has negative curvature. The remaining B vertex also has negative curvature, so must have two incident cuts. This leaves a few possibilities for unfolding, which are dealt with by a case analysis. Possible Unfoldings Summary We study local overlaps in an attempt to simplify analysis of unfoldings and characterize the types of overlaps that can occur in unfoldings. There is a starlike polyhedron with 16 triangular faces for which every unfolding contains a 1local overlap. There exists an ununfoldable, starlike, convexfaced polyhedron with 9 faces.