Download Nonoverlap of the Star Unfolding

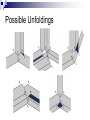
Local Overlaps in
Unfoldings of Polyhedra
Brendan Lucier
Anna Lubiw
University of Waterloo
Presented at the 15th Annual Fall Workshop on
Computational Geometry, 2005
University of Pennsylvania, Philadelphia, PA
Local Overlaps in
Unfoldings of Polyhedra
Brendan Lucier
Anna Lubiw
University of Waterloo
Presented at the 15th Annual Fall Workshop on
Computational Geometry, 2005
University of Pennsylvania, Philadelphia, PA
Outline



Introduction
Avoidability of 1-Local Overlaps
Small Ununfoldable Polyhedron
Outline



Introduction
Avoidability of 1-Local Overlaps
Small Ununfoldable Polyhedron
Unfolding Polyhedra





We consider the act of cutting a polyhedron along its edges and unfolding
it into the plane.
The resulting planar figure is an edge unfolding.
Two faces of the unfolding overlap if they have a common interior point.
An unfolding with no overlap is a simple unfolding, or net.
A polyhedron with no net is referred to as ununfoldable.
Locality of Overlaps




One problem in studying overlaps
is that two faces in vastly different
parts of a polyhedron could
intersect in an unfolding.
We propose a definition of locality
of an overlap.
An overlap is k-local if the
overlapping faces are connected
by a path of k vertices.
In particular, an overlap is 1-local
if the overlapping faces are
coincident with a vertex in the
unfolding.
2-local overlap
1-local overlap
Outline



Introduction
Avoidability of 1-Local Overlaps
Small Ununfoldable Polyhedron
Describing 1-Local Overlaps




A 1-local overlap corresponds precisely to a situation in which a
vertex in an unfolding has total face angle greater than 2π.
To create such an overlap, we must start with a vertex in the
polyhedron with negative curvature, then cut in such a way that one
image of the vertex will retain at least 2π of the surface material.
Convex polyhedra clearly avoid 1-local overlaps, since they contain
no vertices with negative curvature.
Motivating Question: does every polyhedron admit an unfolding that
contains no 1-local overlaps?
No!
Four-Pointed Star



Our polyhedron is a 4-pointed star.
The polyhedron is parameterized:

α is the length of each spike.

β is the height of the center points.
The parameter values are not
important, aside from considering
alpha to be sufficiently large and beta
sufficiently small.
Argument




Claim: every unfolding of the fourpointed star contains a 1-local
overlap.
Each of the four B vertices has
four face angles, each larger than
2π/3.
If three of these faces appeared in
one component of an unfolding,
we have a 1-local overlap
To prevent this, we must cut at
least two opposing edges incident
to each B vertex.
Argument (con’t)





Our cuts cannot make a cycle,
otherwise we get a disconnected
unfolding.
So no two pairs of opposing cuts
can be made to the middle
vertices.
Also, not all pairs can be made to
the points of the star.
The cuts must therefore be made
as shown in the bottom diagram.
There is only one more cut that
can be made, since the set of all
cuts must make a spanning tree
over all vertices.
Argument (con’t)




Note that the center vertices have
negative curvature (they form
saddles).
Each must have at least 2 incident
cuts, otherwise all the face angles
will go to one component and form
a 1-local overlap.
However, our remaining cut
cannot be incident with both
center vertices, since they are not
adjacent.
It is therefore impossible to cut our
4-pointed star to avoid 1-local
overlaps.
Outline



Introduction
(Un)avoidability of 1-Local Overlaps
A Small Ununfoldable Polyhedron
Creating a Smaller Example


The 4-Pointed Star is an ununfoldable
polyhedron with 16 triangular faces.
We shall now make modifications to create a
smaller polyhedron.
 This
polyhedron will remain ununfoldable, but will
avoid 1-local overlaps.

The result will be a starlike ununfoldable
polyhedron with 9 faces.
Modification #1: 3-Pointed Star
Modification #2: Flatten




One side of the polyhedron is
flattened.
Two triangular faces are
combined into a single
quadrilateral face.
Think of the operation as
“cutting” the polyhedron into
two halves, lengthwise.
This introduces the
degeneracy of coplanar faces,
but this can be fixed by
sufficiently small perturbation.
Modification #3: Asymmetricize




Perturb the symmetry of the
points by increasing the angle
between two points.
This adds a new parameter, φ,
indicating the angle change.
We do this to increase the face
angles at two of the B vertices
to larger than 2π/3.
Perturbing by φ = 10o is
sufficient.
Unfolding This Polyhedron




At the B vertices with face
angles greater than 2π/3, two
opposing edges must be cut.
Two cuts must be incident with
the top center vertex, as it has
negative curvature.
The remaining B vertex also
has negative curvature, so
must have two incident cuts.
This leaves a few possibilities
for unfolding, which are dealt
with by a case analysis.
Possible Unfoldings
Summary



We study local overlaps in an attempt to simplify
analysis of unfoldings and characterize the types
of overlaps that can occur in unfoldings.
There is a starlike polyhedron with 16 triangular
faces for which every unfolding contains a 1local overlap.
There exists an ununfoldable, starlike, convexfaced polyhedron with 9 faces.