* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Star Formation
Outer space wikipedia , lookup
Formation and evolution of the Solar System wikipedia , lookup
Cassiopeia (constellation) wikipedia , lookup
Aries (constellation) wikipedia , lookup
Corona Borealis wikipedia , lookup
Auriga (constellation) wikipedia , lookup
Canis Minor wikipedia , lookup
Cygnus (constellation) wikipedia , lookup
Corona Australis wikipedia , lookup
Cosmic distance ladder wikipedia , lookup
Timeline of astronomy wikipedia , lookup
Perseus (constellation) wikipedia , lookup
Future of an expanding universe wikipedia , lookup
Canis Major wikipedia , lookup
Stellar kinematics wikipedia , lookup
Malmquist bias wikipedia , lookup
Stellar classification wikipedia , lookup
H II region wikipedia , lookup
Astronomical spectroscopy wikipedia , lookup
Type II supernova wikipedia , lookup
Standard solar model wikipedia , lookup
Corvus (constellation) wikipedia , lookup
Aquarius (constellation) wikipedia , lookup
Hayashi track wikipedia , lookup
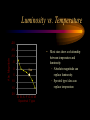
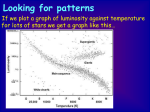
Star Formation Classifying Stars • The surface temperature of a star T is compared to a black body. – Luminosity L – Radius R L 4R 2T 4 • The absolute magnitude calculates the brightness as if the stars were 10 pc away. – Related to luminosity M 2.5 log( L / Lsun ) 4.72 • Type O B A F G K M • Temperature 35,000 K 20,000 K 10,000 K 7,000 K 6,000 K 4,000 K 3,000 K Stellar Relations • Some bright stars – Sun – Sirius – Alpha Centauri – Capella – Rigel – Betelgeuse – Aldebaran (class) G2 A1 G2 G8 B8 M1 K5 (absolute magnitude) 4.8 1.4 4.1 0.4 -7.1 -5.6 -0.3 Luminosity vs. Temperature -20 -15 Abs. Magnitude -10 -5 0 Sun 5 10 15 20 O B A F G K M Spectral Type • Most stars show a relationship between temperature and luminosity. – Absolute magnitude can replace luminosity. – Spectral type/class can replace temperature. Hertzsprung-Russell Diagram • The chart of the stars’ luminosity vs. temperature is called the Hertzsprung-Russell diagram. • This is the H-R diagram for hundreds of nearby stars. – Temperature decreases to the right Main Sequence -20 • Most stars are on a line called the main sequence. -15 Abs. Magnitude -10 -5 0 Sirius 5 1 solar radius 10 15 20 O B A F G K M Spectral Type • The size is related to temperature and luminosity: – hot = large radius – medium = medium radius – cool = small radius Giants -20 -15 Abs. Magnitude -10 Rigel -5 0 5 supergiants Betelgeuse giants Aldebaran Capella 10 15 20 O B A F G K M Spectral Type • Stars that are brighter than expected are large and are called giants or supergiants. • Betelgeuse is a red supergiant with a radius hundreds of times larger than the sun. Dwarves -20 • Stars on the main sequence that dim and cool are red dwarves. -15 Abs. Magnitude -10 -5 • Small, hot stars that are dim are not on the main sequence and are called white dwarves. 0 5 10 15 20 white dwarves O B A F G K M Spectral Type Interstellar Medium • Interstellar space is filled with gas (99%) and dust (1%). • Interstellar gas, like the sun, is 74% hydrogen and 25% helium. • Interstellar dust, like clouds in the gas giants, are molecular carbon monoxide, ammonia, and water. • Traces of all other elements are present. • Atoms are widely spaced, about 1 atom per cm3, a nearly perfect vacuum. • The temperature is cold, less than 100 K. Molecular Clouds • The small mass of atoms creates very weak gravity. • Gravity can pull atoms and molecules together. • Concentrations equal to 1 million solar masses can form giant molecular clouds over 100 ly across. Catalysts for Star Formation • A cool (10 K) nebula can be compressed by shock waves. • These shock waves are from new stars and exploding supernovae. exploding star shock waves nebula with areas of higher density Gravitational Contraction • Density fluctuations cause mass centers to appear. r m(r ) (r)4r 2 dr 0 • Mass at a distance will be accelerated by gravity. • If there is no outward pressure there will be free fall. – Mass m0 within radius r – Conservation of energy – Calculate free fall time g (r ) Gm(r ) r2 2 1 dr Gm0 Gm0 2 dt r r0 0 2Gm 2Gm0 dt 0 dr r0 dr r0 r r 0 0 3 32G 0 1 2 dr Protostars • Local concentrations in a nebula can be compressed by gravity. With low temperature they don’t fly apart again. – Contracting material forms one or more centers – The contracting material begins to radiate – These are protostars, called T Tauri stars (G, K, M). Hydrostatic Equilibrium dP Gm(r ) (r ) dr r2 R R 0 0 R Gm( r ) dP 4r dm 2 0 dr r 3 4r 3 dP 3 P V dr 3 P V Egrav P E grav 3V • Gravity is balanced by pressure. – Equilibrium condition – True at all radii • The left side is related to average pressure. – Integrated by parts • The right side is the gravitational potential energy. Adiabatic Index • Adiabatic compression is not linear in pressure and volume. – Parameter g is adiabatic index – Relate to internal energy • The gravitational energy was also related to the pressure. – Energy condition for equilibrium g dV dP 0 V P 1 dEint PdV d ( PV ) g 1 E P (g 1) int V E grav 3V (g 1) Eint V E grav 3(g 1) Eint 0 Formation Conditions E grav Eint • Contraction requires gravitational energy to exceed internal energy. – Thermal kinetic energy 3kT/2 GM 2 E grav f R M min 3kT R 2Gm 3 3kT J 4M 2 2Gm 3 • The conditions for cloud collapse follow from mass or density. – Jeans mass, density MJ, J Fusion Begins • Initial energy is absorbed by hydrogen ionization. – eD = 4.5 eV – eI = 13.6 eV • Apply this to hydrostatic equilibrium. • Continued contraction results in quantum electron gas. – When degenerate it resists compression – Sets temperature at core EI M M eD eI 2 mH mH kT 1 e D 2e I 2.6 eV 12 (me kT )3 2 m h3 G 2 m 8 3me 4 3 M kT 2 h Birth of the Sun -20 • Gravity continues to pull the gas together. – Temperature and density increases -15 Abs. Magnitude -10 -5 0 1 M • If the temperature at the center becomes 5 million degrees then hydrogen fusion begins. 5 10 15 20 O B A F G K M Spectral Type • At this point the star has reached the main sequence. Birth of Other Stars -20 -15 Abs. Magnitude -10 -5 10 M 0 3 M 0.5 M 5 10 0.02 M 15 20 O B A F G K M Spectral Type • Large masses become brighter, hotter stars. • Gravity causes fusion to start sooner, about 100,000 years. • Small masses become dimmer, cooler stars. • Gravity takes longer to start fusion, up to 100 million years.