Download ICDM04Stream

Decision Tree Evolution using Limited
number of Labeled Data Items
from Drifting Data Streams
Wei Fan1, Yi-an Huang2, and Philip S. Yu1
1IBM
T.J.Watson
2Georgia Tech
“Sad” life cycle of inductive models
Inductive
Learner
Labeled
Data
•
•
•
Decision Trees
Rules
Naïve Bayes
Accuracy
too low!!!
True
Labels
Inductive
Model
Credit card transaction ->
{fraud, normal}
God
knows
the
accuracy
Predictions
Un-labeled
Real-time
Streaming
Data
Seen any problems?
 Problem 1: we have no idea of the
accuracy in the streaming
environment.
 Problem 2: how long we can wait and
how much we can afford to loose until
we get labeled data?
Solutions
 Solution I: error guessing and estimation.
 Idea 1: using observable statistical traits from
the model itself to guess the error on unlabeled
streaming data.
 Idea 2: using very small number of specifically
acquired examples to statistically estimate the
error – similar to estimate poll to estimate Bush
or Kerry will win the presidency.
 Details: “Active Mining of Data Streams” by Wei
Fan, Yi-an Huang, and Philip S. Yu appearing in
SDM’04.
Solutions
 Okay, assuming that we know that
our model is too low in accuracy.
 Obviously, we need more accurate
models.
 Solution II:
 We need to update our model with
limited number of training examples
 We are interested in decision trees.
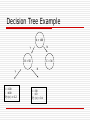
Decision Tree Example
A < 100
N
Y
B < 50
y
+: 100
- : 400
P(+|x) = 0.2
C < 34
N
+: 90
- : 10
P(-|x) = 0.1
Class Distribution Replacement
 If a node is considered “suspicious”
using one of our detection techniques,
we can perform class distribution
replacement.
 The idea is that:
Class Distribution Replacement
A < 100
N
Y
B < 50
y
+: 100
- : 400 = 0.4
P(+|x)
P(+|x) = 0.2
C < 34
N
Using limited
number of
examples, the new
class distribution
is
+: 90
P(+|x)
- :=100.4
P(-|x) = 0.1
Some Statistics for Significance Test
 Proportion
statistics: formula
is in paper and
many statistics
books.
 Assume Gaussian
distribution and
compute
significance
Leaf Expansion
 Assume that significance test in leaf
expansion fails.
 Solution: reconstruct the leaf using
limited number of examples.
 Catch: not always possible. If the limited
number of examples cannot justify an
expansion, just keep the original node.
Result on Class Distribution Replacement
Result on Leaf Node Expansion
More results in the paper
 Credit card fraud dataset.
 UCI Adult Dataset.
Conclusion
 Pointed out the “gap” between data
availability and pattern change.
 Proposed a general framework.
 Proposed a few methods to update
and grow a decision tree from limited
number of examples.