Survey
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Angle Bisector Theorem (notes)
Document related concepts
Noether's theorem wikipedia , lookup
Multilateration wikipedia , lookup
Geometrization conjecture wikipedia , lookup
Euler angles wikipedia , lookup
Perceived visual angle wikipedia , lookup
Line (geometry) wikipedia , lookup
List of works designed with the golden ratio wikipedia , lookup
History of trigonometry wikipedia , lookup
Golden ratio wikipedia , lookup
Rational trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
History of geometry wikipedia , lookup
Integer triangle wikipedia , lookup
Transcript
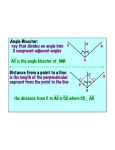
GEOMETRY Notes: Angle Bisector Theorem Notes: Angle Bisector Theorem In a triangle the angle bisector divides the opposite side in the ratio of the remaining sides. This ABC ( figure 5.5) the bisector of A divides BC in the ratio . Figure 5.5 To prove that Through C draw a line parallel to seg.AD and extend seg.BA to meet it at E. seg.CE seg.DA BAD AEC , corresponding angles DAC ACE , alternate angles But BAD = DAC , given AEC ACE Hence AEC is an isosceles triangle. seg.AC seg.AE Instructor: CHRISTLE MAE B. OCHIGUE [email protected] In BCE AD CE Thus the bisector divides the opposite side in the ratio of the remaining two sides. Source: http://www.pinkmonkey.com/studyguides/subjects/geometry/chap5/g0505501.asp Instructor: CHRISTLE MAE B. OCHIGUE [email protected]
